В C# задача поиска минимального элемента массива решается с использованием различных подходов в зависимости от требований к производительности и читаемости кода. Наиболее очевидный способ заключается в использовании цикла для последовательного сравнения элементов массива. Такой метод прост в реализации и хорошо работает для небольших массивов. Однако для больших данных стоит учитывать более эффективные алгоритмы и встроенные возможности .NET.
Основной алгоритм заключается в последовательном просмотре всех элементов массива. Для этого можно пройти по каждому элементу и на каждом шаге сравнивать его с текущим минимальным значением. Если текущий элемент меньше, обновляется минимальное значение. Этот подход имеет сложность O(n), где n – количество элементов в массиве.
В C# для поиска минимального значения можно использовать встроенный метод Min() из пространства имен System.Linq. Этот метод позволяет легко найти минимальное значение без необходимости вручную реализовывать цикл. Однако стоит помнить, что использование LINQ может быть менее производительным, чем собственная реализация, если массив очень большой или если нужна максимальная скорость работы.
Рекомендация: для оптимизации кода в случаях, когда важно минимизировать использование памяти или уменьшить время выполнения, можно обойтись без LINQ и использовать стандартный цикл. Это обеспечит полный контроль над процессом и избавит от накладных расходов, связанных с дополнительной абстракцией.
Использование метода Array.Min() для поиска минимума
Для использования метода Array.Min() необходимо подключить пространство имен System.Linq, так как этот метод реализован именно в нем. Важно отметить, что Array.Min() работает только с массивами, содержащими элементы, которые могут быть сравнены между собой (например, числа, строки).
Пример использования метода для нахождения минимального числа в массиве:
using System;
using System.Linq;
class Program
{
static void Main()
{
int[] numbers = { 5, 8, 1, 9, 2 };
int min = numbers.Min();
}
}Если в массиве есть отрицательные числа или значения с плавающей точкой, метод также корректно находит минимальное значение:
double[] values = { -2.5, 3.1, 0.9, -4.6 };
double minValue = values.Min();
Метод Min() может быть использован не только для стандартных типов данных, но и для более сложных структур. Например, если требуется найти минимальный элемент в коллекции объектов, нужно использовать лямбда-выражения:
class Person
{
public string Name { get; set; }
public int Age { get; set; }
}
var people = new List
{
new Person { Name = "Alice", Age = 30 },
new Person { Name = "Bob", Age = 25 },
new Person { Name = "Charlie", Age = 35 }
};
var youngest = people.Min(p => p.Age);
Метод Array.Min() эффективно работает только с одномерными коллекциями. Для многомерных массивов или коллекций можно использовать подход с дополнительными вычислениями или же перебором элементов вручную. Важно также помнить, что если массив пуст, метод Min() вызовет исключение InvalidOperationException.
Для безопасного поиска минимального значения в возможном пустом массиве можно использовать сочетание с методом DefaultIfEmpty(), чтобы задать значение по умолчанию:
int[] emptyArray = { };
int minEmpty = emptyArray.DefaultIfEmpty().Min();
Таким образом, Array.Min() – это быстрый и простой способ найти минимальное значение в массиве. Он удобно работает с типами данных, поддерживающими сравнение, и легко расширяется с помощью лямбда-выражений для более сложных объектов.
Как найти минимальный элемент вручную с помощью цикла
Чтобы найти минимальный элемент массива вручную, можно использовать цикл, который будет поочередно проверять каждый элемент и обновлять минимальное значение, если текущий элемент меньше уже найденного минимума.
Алгоритм состоит из нескольких шагов:
- Инициализация переменной для хранения минимального элемента, например, первым элементом массива.
- Проход по всем элементам массива с использованием цикла.
- На каждой итерации сравнение текущего элемента с минимальным значением. Если текущий элемент меньше минимального, обновляем минимальное значение.
- После завершения цикла минимальное значение будет содержать минимальный элемент массива.
Пример кода для нахождения минимального элемента:
int[] numbers = { 5, 3, 9, 1, 7 };
int min = numbers[0]; // Инициализация минимального элемента
for (int i = 1; i < numbers.Length; i++)
{
if (numbers[i] < min)
{
min = numbers[i]; // Обновление минимального значения
}
}
Console.WriteLine("Минимальный элемент: " + min);
Рекомендации:
- Начинать цикл с первого элемента массива, так как для корректного сравнения требуется инициализировать минимальное значение.
- Если в массиве есть отрицательные числа, алгоритм работает так же эффективно, как и с положительными.
- В случае с пустым массивом необходимо заранее проверять его длину, чтобы избежать ошибок выполнения.
Обработка пустого массива при поиске минимального значения
Когда мы пытаемся найти минимальный элемент в массиве, важно учитывать случай, когда массив может быть пустым. В таких ситуациях попытка получить минимальное значение без предварительной проверки приведет к ошибке выполнения. Чтобы избежать этого, необходимо внедрить обработку таких случаев в код.
В C# для нахождения минимального элемента обычно используется метод Enumerable.Min() из пространства имен System.Linq. Однако при работе с пустым массивом этот метод выбрасывает исключение InvalidOperationException, так как не может найти минимальное значение в отсутствующих данных. Чтобы избежать ошибок, следует предусмотреть проверку на пустоту массива до вызова метода.
Вот несколько вариантов правильной обработки пустого массива:
- Использование условного оператора
ifдля проверки массива на пустоту перед вызовом методаMin():
int[] array = new int[] { };
if (array.Length == 0) {
Console.WriteLine("Массив пустой.");
} else {
int min = array.Min();
Console.WriteLine("Минимальное значение: " + min);
}
- Использование метода
Any()из LINQ для проверки, есть ли элементы в массиве:
if (!array.Any()) {
Console.WriteLine("Массив пустой.");
} else {
int min = array.Min();
Console.WriteLine("Минимальное значение: " + min);
}
Также можно задать возвращаемое значение по умолчанию в случае пустого массива, если логика программы это позволяет. Например, можно вернуть int.MinValue или другое значение, которое будет сигнализировать о проблеме с данным массивом:
int min = array.Length == 0 ? int.MinValue : array.Min();
Console.WriteLine(min == int.MinValue ? "Массив пустой." : "Минимальное значение: " + min);
Выбор метода зависит от требований к программе и от того, как важно правильно обработать пустой массив. В любом случае важно предусмотреть этот случай, чтобы избежать неожиданного поведения приложения.
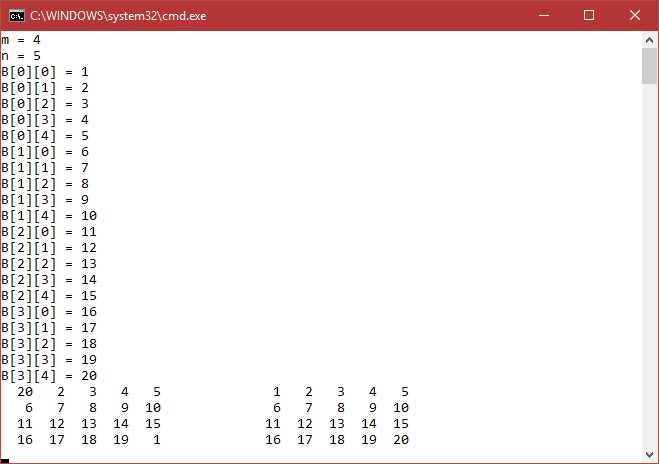
Поиск минимального элемента в многомерном массиве
При работе с многомерными массивами в C# поиск минимального элемента может быть сложнее, чем в одномерных, из-за структуры данных. Многомерные массивы, например, двумерные или трехмерные, требуют особого подхода для поиска минимального значения. Чтобы эффективно находить минимальный элемент в таком массиве, важно правильно организовать обход элементов и учитывать размерность массива.
Для начала определим, что такое многомерный массив. Это массив, элементы которого сами являются массивами. Например, двумерный массив – это массив массивов, где каждый элемент представляет собой строку (или столбец) данных.
Для поиска минимального значения в двумерном массиве можно использовать цикл, который будет перебирать все строки и столбцы, сравнивая элементы на каждом шаге. Важно помнить, что на каждой итерации цикла необходимо обновлять переменную, хранящую минимальное значение, если текущий элемент меньше найденного минимума.
Пример кода для поиска минимального элемента в двумерном массиве:
int[,] array = {
{3, 5, 1},
{8, 2, 6},
{4, 9, 7}
};
int min = array[0, 0];
for (int i = 0; i < array.GetLength(0); i++)
{
for (int j = 0; j < array.GetLength(1); j++)
{
if (array[i, j] < min)
{
min = array[i, j];
}
}
}
Console.WriteLine($"Минимальное значение: {min}");
В данном примере мы сначала предполагаем, что минимальное значение – это элемент в первой ячейке массива. Затем с помощью вложенных циклов (для строк и столбцов) мы проверяем все элементы массива и обновляем минимальное значение при нахождении меньшего элемента.
Этот подход можно адаптировать для массивов любой размерности. Для трехмерных и более сложных массивов также используют вложенные циклы для каждой из измерений, увеличивая количество циклов, соответствующих размерности массива.
В случае если размерность массива неизвестна заранее, можно использовать рекурсивный алгоритм, который будет обходить массив, независимо от того, сколько измерений у него есть. Однако стоит помнить, что рекурсия может быть менее эффективной для очень больших массивов из-за потенциального переполнения стека вызовов.
Как учесть возможные ошибки при сравнении элементов массива

Первое, на что стоит обратить внимание, это тип данных элементов массива. Например, если в массиве содержатся числа с плавающей точкой (float или double), возможны ошибки при сравнении из-за погрешностей округления. Для решения этой проблемы следует использовать метод сравнения с учетом заданной точности (например, использовать функцию, которая сравнивает числа с учетом допустимой погрешности).
Пример:
float epsilon = 0.0001f;
if (Math.Abs(a - b) < epsilon) {
// a и b считаются равными
}
Также важно проверять наличие значений, которые могут быть исключением, например, null или NaN. При сравнении элементов массива с такими значениями могут возникнуть ошибки, если не учесть их заранее. Для этого стоит использовать дополнительные проверки на null перед попыткой сравнения или обработать особые случаи для NaN.
Пример:
if (a == null || b == null) {
// Обработка случая null
}
if (float.IsNaN(a) || float.IsNaN(b)) {
// Обработка NaN
}
Если сравниваются элементы массива разных типов (например, целые числа и числа с плавающей точкой), нужно четко понимать, что при преобразовании типов могут возникнуть потери данных. Чтобы избежать ошибок, лучше заранее привести все элементы массива к одному типу, который точно подходит для сравнения.
Не менее важным моментом является порядок выполнения операций. Если массив содержит очень большие или очень маленькие числа, и вы используете стандартные операторы сравнения, возможны переполнения или потеря значимости данных. Для защиты от таких ситуаций можно использовать стандартные функции, которые проверяют переполнение (например, метод Checked в C#), или работать с типами данных, которые специально предназначены для хранения значений с высокой точностью.
В завершение стоит упомянуть, что при поиске минимального элемента массива всегда стоит учитывать не только правильность алгоритма, но и обработку возможных ошибок, связанных с особенностями типов данных и их преобразований. Правильное использование проверок и вспомогательных методов сделает код более надежным и безопасным.
Алгоритмы поиска минимального значения в отсортированном массиве

В случае отсортированного массива поиск минимального элемента значительно упрощается. В зависимости от типа сортировки (по возрастанию или убыванию), алгоритм будет различаться.
Для массива, отсортированного по возрастанию, минимальное значение всегда находится на первом индексе. Достаточно выполнить доступ к элементу с индексом 0 для получения минимального значения. Это решение имеет время выполнения O(1), так как доступ к элементам массива осуществляется за постоянное время.
Когда массив отсортирован по убыванию, минимальный элемент будет расположен на последнем индексе. Для получения его также достаточно обращения к элементу с индексом, равным длине массива минус один. Это также выполняется за O(1) времени.
Если требуется использование алгоритмов поиска в больших данных с дополнительными ограничениями (например, бинарный поиск), стоит учитывать, что бинарный поиск, применяемый к отсортированным массивам, позволяет быстро находить не только минимальные, но и другие элементы. Однако для задачи нахождения минимального значения в отсортированном массиве бинарный поиск не всегда применим, так как его основной смысл – нахождение элемента по условию, а не вычисление минимума в однозначно упорядоченном наборе данных.
Для многомерных массивов или массивов с неравномерной сортировкой (например, отсортированных по частям), решение задачи может потребовать более сложных алгоритмов, таких как модификация бинарного поиска для работы с локальными минимальными значениями или использование методов слияния. В этом случае подходы зависят от особенностей сортировки.
Таким образом, при работе с отсортированными массивами, задача нахождения минимального элемента сводится к простому обращению к первому или последнему элементу массива в зависимости от порядка сортировки. Алгоритмическая сложность решения этой задачи остается минимальной – O(1).