В Python округление чисел – это часто используемая операция, необходимая для корректного представления данных, особенно в математических вычислениях, финансовых приложениях или научных расчетах. Важно правильно управлять точностью чисел, чтобы избежать ошибок при их дальнейшей обработке. Для этого язык предоставляет несколько инструментов, позволяющих округлять числа до нужного количества знаков после запятой.
Основной метод округления в Python реализован в функции round(). Этот инструмент позволяет округлять числа до определенного числа знаков после запятой. Например, вызов round(3.14159, 2) вернет значение 3.14. Однако стоит помнить, что функция использует так называемое округление «по банку» (round half to even), что иногда может привести к неожиданным результатам при работе с числами, заканчивающимися на 5.
Для более точного контроля над округлением можно использовать модуль decimal, который предоставляет класс Decimal для работы с числами с фиксированной точностью. Это особенно полезно в финансовых вычислениях, где критична точность. Метод quantize() в классе Decimal позволяет задавать количество знаков после запятой с точностью до единичного разряда, и таким образом избежать проблем округления, характерных для стандартных типов данных с плавающей запятой.
Кроме того, для решения специфических задач, таких как округление в сторону бесконечности или к нулю, можно использовать другие математические методы из библиотеки math, например, функции floor() и ceil(), которые округляют числа вниз или вверх соответственно.
Использование функции round() для округления до заданного числа знаков
Синтаксис функции выглядит так: round(number, ndigits), где number – это число, которое требуется округлить, а ndigits – количество знаков после запятой. Если параметр ndigits не указан, функция округляет число до ближайшего целого.
Пример использования:
round(3.14159, 2) # Результат: 3.14Функция round() использует правила округления, где числа, находящиеся на границе между двумя значениями, округляются к ближайшему чётному числу. Например, round(2.5) вернёт 2, а round(3.5) – 4.
При работе с функцией round() стоит учитывать, что она может не всегда вести себя интуитивно при округлении чисел с плавающей точкой. Например, результат округления числа round(0.675, 2) может оказаться 0.67 вместо ожидаемого 0.68 из-за особенностей представления чисел с плавающей точкой в компьютерах.
Для повышения точности округления рекомендуется использовать функцию round() в сочетании с другими методами работы с числами, например, с использованием библиотеки decimal для более сложных вычислений с фиксированной точностью.
Как округлить число до целого с помощью функции int()
Функция int() в Python используется для преобразования числа с плавающей точкой в целое число. При этом дробная часть числа отбрасывается, а сам результат всегда представляет собой ближайшее целое число, которое меньше или равно исходному значению. Рассмотрим основные моменты при использовании этой функции.
Пример использования:
x = 3.75
y = int(x) # y = 3Функция int() не выполняет округление в классическом смысле, как, например, функция round(). Она просто отбрасывает дробную часть числа:
- При вызове
int(4.99)результатом будет4. - При вызове
int(-4.99)результатом будет-4.
Важно отметить, что int() всегда округляет в сторону меньшего целого числа. Это отличие от округления по математическим правилам, где дробная часть числа может быть округлена в большую сторону, если она больше или равна 0.5.
Когда использовать int():
- Если нужно просто отбросить дробную часть без выполнения округления.
- Когда результатом должно быть целое число, независимо от знака и величины дробной части.
- Для преобразования строк, представляющих целые числа, в тип
int.
Пример с преобразованием строки:
string_value = "45.67"
int_value = int(float(string_value)) # сначала преобразуем в float, затем в intИспользование int() подходит в случаях, когда не требуется сложная логика округления и необходим только целый результат, полученный без учета дробной части.
Округление чисел с использованием модуля decimal
Модуль decimal в Python предоставляет средства для работы с десятичными числами с высокой точностью. Округление чисел с помощью этого модуля позволяет избежать проблем, связанных с ограниченной точностью стандартных типов данных, таких как float. Использование decimal подходит для финансовых расчетов, где важно соблюдать точность и избежать ошибок округления.
Для округления чисел в decimal используется метод quantize(). Он позволяет задавать точность округления, указывая нужное количество знаков после запятой. Этот метод принимает два аргумента: объект Decimal, к которому применяется округление, и другой объект Decimal, который определяет формат округления. Второй объект представляет собой шаблон для округления, например, число с нужным количеством знаков после запятой.
Пример:
from decimal import Decimal, ROUND_HALF_UP
number = Decimal('12.34567')
rounded_number = number.quantize(Decimal('0.01'), rounding=ROUND_HALF_UP)
print(rounded_number)
В данном примере число 12.34567 округляется до двух знаков после запятой с использованием правила округления ROUND_HALF_UP, что дает результат 12.35.
Для указания различных типов округления в quantize() можно использовать следующие параметры:
ROUND_HALF_UP– округление «вверх» при 0.5 и выше;ROUND_HALF_DOWN– округление «вниз» при 0.5 и ниже;ROUND_DOWN– всегда округление вниз;ROUND_UP– всегда округление вверх;ROUND_HALF_EVEN– округление к ближайшему четному числу;ROUND_FLOOR– округление вниз к ближайшему числу.
При использовании метода quantize() важно, чтобы второй аргумент был объектом Decimal с точно определенным количеством знаков после запятой. Если попытаться передать обычное число или строку, это вызовет ошибку.
Для выполнения более сложных операций с округлением можно использовать контексты округления. Контекст округления определяет поведение всех операций округления в рамках программы. Контекст можно задать через getcontext() и изменить параметры, такие как точность и метод округления. Пример:
from decimal import getcontext, ROUND_HALF_UP
getcontext().prec = 5
getcontext().rounding = ROUND_HALF_UP
number = Decimal('12.3456789')
rounded_number = number + Decimal('0.00001')
print(rounded_number)
Этот пример устанавливает общую точность в 5 знаков и округляет результат согласно правилам ROUND_HALF_UP. В результате будет выведено значение с учетом всех настроек контекста.
Использование модуля decimal рекомендуется при необходимости работы с числами, где критична точность, например, в финансовых приложениях или расчетах, требующих строго определенного округления.
Решение проблемы округления с потерей точности в Python

Округление чисел в Python может вызывать проблемы с точностью, особенно при работе с десятичными дробями. Это связано с тем, что числа с плавающей запятой в языке хранятся в двоичной форме, что может приводить к неточностям при преобразованиях. Например, числа типа float могут быть представлены не точно из-за ограничений памяти и алгоритмов хранения.
Один из распространённых способов решения этой проблемы – использование модуля decimal, который предоставляет более точное представление чисел с фиксированной точностью. Вместо стандартного типа float рекомендуется использовать тип Decimal из модуля decimal, который позволяет задавать точность вычислений и минимизировать ошибки округления.
Пример использования:
from decimal import Decimal, getcontext
getcontext().prec = 6 # Установка точности вычислений
a = Decimal('0.1') + Decimal('0.2')
В этом примере значение 0.1 и 0.2 точно представляются как объекты Decimal, что позволяет избежать потери точности при вычислениях.
Ещё одним подходом является использование модуля fractions, который позволяет работать с числами в виде дробей. Это может быть полезно, если необходимо работать с дробными значениями без потери точности, особенно при математических вычислениях, требующих высокой точности.
Пример использования:
from fractions import Fraction
a = Fraction(1, 10)
b = Fraction(2, 10)
result = a + b
Для простых задач округления, где важна точность до нескольких знаков после запятой, можно использовать встроенную функцию round(). Однако важно понимать, что она не решает проблему потери точности в вычислениях, а лишь округляет результат до нужного числа знаков.
Пример:
x = 1.23456789
rounded_x = round(x, 4)
Для предотвращения потери точности при сложных вычислениях всегда выбирайте подходящие типы данных, такие как Decimal или Fraction, которые лучше справляются с точностью и округлением чисел в Python.
Как округлить числа в сторону «ближайшего чётного»

Округление в сторону ближайшего чётного числа (также известное как округление по правилам Банкера) используется, чтобы уменьшить систематическую погрешность в вычислениях. Это особенно важно при обработке больших объёмов данных, чтобы избежать накопления ошибок округления.
В Python для округления числа к ближайшему чётному можно использовать функцию round(). Эта функция округляет число до указанного количества знаков после запятой, но в случае, если число точно посередине между двумя возможными значениями, оно округляется в сторону ближайшего чётного числа.
Пример:
Рассмотрим числа, которые могут быть округлены до 1 знака после запятой:
round(2.5, 1) # вернёт 2.0
round(3.5, 1) # вернёт 4.0
round(1.5, 1) # вернёт 2.0
round(2.35, 1) # вернёт 2.4
Здесь, числа 2.5 и 3.5 округляются в сторону ближайших чётных чисел: 2 и 4 соответственно.
Почему это работает?
Когда число находится ровно посередине между двумя целыми числами, Python выбирает чётное число, чтобы минимизировать ошибки округления в больших вычислениях. Например, 2.5 округляется до 2, а не до 3, так как 2 является чётным числом.
Это поведение встроенной функции round() в Python часто используется в финансовых расчётах и других областях, где важно избежать систематических отклонений при многократных округлениях.
Особенности использования:
Если вам необходимо округлить числа в другом направлении, например, всегда в большую сторону или всегда в меньшую, стоит использовать функции math.ceil() или math.floor(). Однако, для большинства задач округление к ближайшему чётному подходит идеально и позволяет избежать случайных отклонений в длительных вычислениях.
Округление чисел при работе с денежными суммами в Python
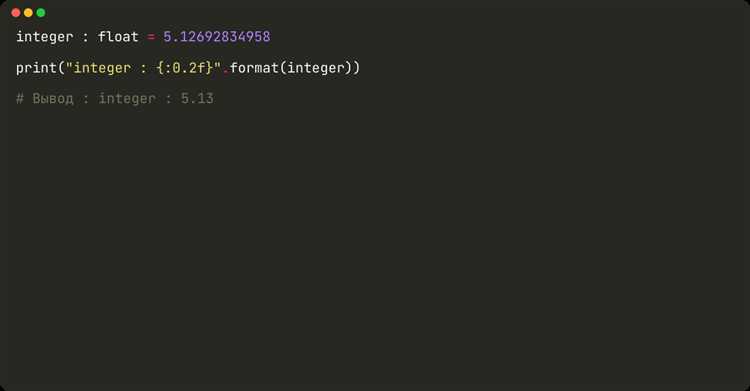
При работе с денежными суммами в Python важно учитывать точность округления, чтобы избежать ошибок при расчетах. Денежные значения часто имеют ограниченную точность, так как они обычно включают только два знака после запятой. Для этого в Python используется несколько методов округления чисел, каждый из которых подходит для различных сценариев.
Один из наиболее надежных способов округления денежных сумм – использование встроенной функции round(). Она позволяет округлять число до заданного количества знаков после запятой. Например, если нужно округлить сумму до двух знаков после запятой, можно применить следующий код:
summa = 123.4567
rounded_summa = round(summa, 2)
print(rounded_summa) # 123.46Тем не менее, round() может вести себя неожиданно в некоторых случаях из-за особенностей представления чисел с плавающей точкой. Это явление связано с тем, как Python хранит числа в памяти. Например, округление round(2.675, 2) может дать 2.67 вместо ожидаемых 2.68.
Для более точного округления, особенно в финансовых приложениях, рекомендуется использовать модуль decimal, который работает с фиксированной точностью. Этот модуль подходит для денежных расчетов, поскольку он позволяет задать точность и избежать ошибок при округлении, связанных с числами с плавающей точкой. Для округления можно использовать метод quantize():
from decimal import Decimal, ROUND_HALF_UP
summa = Decimal('123.4567')
rounded_summa = summa.quantize(Decimal('0.01'), rounding=ROUND_HALF_UP)
print(rounded_summa) # 123.46В примере используется метод quantize() с округлением по правилам ROUND_HALF_UP, что является стандартным способом округления в денежных расчетах. Это гарантирует, что числа округляются в сторону большего значения, если последняя цифра равна или больше 5.
Для обеспечения корректности расчетов при работе с большими суммами и конверсией валют лучше использовать именно decimal, а не стандартные типы данных Python. Важно всегда указывать точность, с которой работает система, чтобы избежать накопления погрешностей в длинных вычислениях.