При решении задач, связанных с прямоугольными треугольниками, часто требуется найти длину гипотенузы по известным катетам. В Python это можно сделать с минимальным количеством кода, используя встроенные математические функции. Стандартная библиотека math содержит функцию hypot(), которая возвращает гипотенузу без необходимости вручную возводить числа в квадрат и извлекать корень.
![При решении задач, связанных с прямоугольными треугольниками, часто требуется найти длину гипотенузы по известным катетам. В Python это можно сделать с минимальным количеством кода, используя встроенные математические функции. Стандартная библиотека undefinedmath</em> содержит функцию <strong>hypot()</strong>, которая возвращает гипотенузу без необходимости вручную возводить числа в квадрат и извлекать корень.»></p>
<p>Пример простейшего вычисления:</p>
<pre><code>import math
a = 3
b = 4
c = math.hypot(a, b)
print(c) # Результат: 5.0
</code></pre>
<p>Функция <strong>math.hypot()</strong> автоматически обрабатывает точность вычислений и избегает переполнения, что делает её предпочтительным выбором по сравнению с выражением <em>(a<strong>2 + b</strong>2)<strong>0.5</em>. В задачах с большим количеством входных данных или при обработке координат в двумерном пространстве эта функция обеспечивает стабильность и читаемость кода.</p>
<p>Если подключение сторонних библиотек допустимо, можно использовать <strong>numpy.hypot()</strong>, особенно при работе с массивами:</p>
<pre><code>import numpy as np
a = np.array([3, 5])
b = np.array([4, 12])
c = np.hypot(a, b)
print(c) # Результат: [ 5. 13.]
</code></pre>
<p>Этот подход удобен в случаях, когда нужно обработать сразу несколько пар значений. <strong>numpy.hypot()</strong> применяется поэлементно, что упрощает работу с векторами и матрицами.</p>
<p>Выбор между <em>math</em> и <em>numpy</em> зависит от контекста: для одиночных значений достаточно стандартной библиотеки, для массивов – <em>numpy</em> предпочтительнее.</p>
<h2>Как вычислить гипотенузу по теореме Пифагора с использованием встроенных операторов</h2>
<p><img decoding=](/wp-content/images5/kak-najti-gipotenuzu-v-python-f287q8tk.jpg)
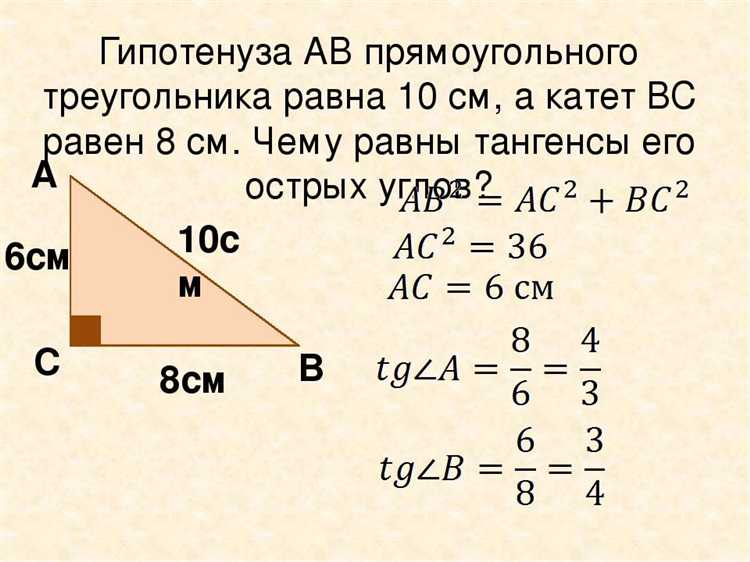
Для вычисления гипотенузы достаточно применить теорему Пифагора: квадрат гипотенузы равен сумме квадратов катетов. В Python это реализуется без дополнительных библиотек, используя базовые арифметические операторы.
- Задать значения двух катетов. Они могут быть введены пользователем или заданы напрямую.
- Возвести каждый катет в квадрат с помощью оператора
. - Сложить полученные квадраты.
- Извлечь квадратный корень из суммы с помощью оператора возведения в степень
0.5.
Пример:
a = 3
b = 4
c = (a2 + b2)0.5
print(c) # Результат: 5.0
- Переменные
aиb– длины катетов. - Оператор
используется как для возведения в квадрат, так и для извлечения корня. - Тип результата –
float, даже если ввод – целые числа.
Если требуется округление, можно использовать round(c, n), где n – количество знаков после запятой.
print(round(c, 2)) # Результат: 5.0
Применение модуля math для извлечения квадратного корня
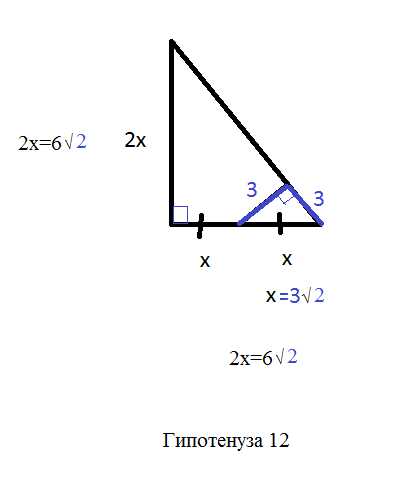
Для вычисления гипотенузы в прямоугольном треугольнике часто используют теорему Пифагора: c = √(a² + b²). В Python модуль math предоставляет функцию sqrt(), которая возвращает квадратный корень от числа типа float.
Подключение модуля выполняется через import math. Вызов math.sqrt(x) требует, чтобы x было неотрицательным числом. При передаче отрицательного значения произойдёт ValueError. Для обработки ошибок используют конструкцию try-except.
Пример: math.sqrt(25) возвращает 5.0. В случае гипотенузы: math.sqrt(a2 + b2). Если a = 3 и b = 4, результат будет 5.0.
Для точных вычислений предпочтительнее использовать math.sqrt(), а не оператор возведения в степень 0.5, поскольку функция из модуля math оптимизирована для работы с числами с плавающей точкой.
Обработка пользовательского ввода для расчёта гипотенузы
Для получения данных от пользователя используется функция input(). Ввод необходимо привести к числовому типу, так как изначально возвращается строка. Пример: a = float(input("Введите длину первого катета: ")).
Чтобы избежать сбоев при вводе некорректных значений, требуется использовать конструкцию try-except. Это позволяет отлавливать ошибки преобразования типов:
try:
a = float(input("Введите первый катет: "))
b = float(input("Введите второй катет: "))
except ValueError:
print("Ошибка: необходимо ввести числовое значение.")
Также необходимо проверить, что введённые числа положительные. Проверка выполняется сразу после преобразования:
if a <= 0 or b <= 0:
print("Катеты должны быть положительными числами.")
При необходимости можно вынести ввод в отдельную функцию, которая будет возвращать корректные значения только после прохождения всех проверок:
def получить_катет(имя):
while True:
try:
значение = float(input(f"Введите {имя} катет: "))
if значение > 0:
return значение
else:
print("Значение должно быть положительным.")
except ValueError:
print("Ошибка: введите число.")Пример использования: a = получить_катет("первый"), b = получить_катет("второй").
Такой подход предотвращает завершение программы при ошибке и гарантирует получение подходящих данных для дальнейших расчётов.
Округление результата до заданного количества знаков после запятой
Для округления значения гипотенузы используется встроенная функция round(). Она принимает два аргумента: число и количество знаков после запятой. Например, round(hypotenuse, 3) вернёт результат с точностью до тысячных.
При работе с большим количеством данных округление можно выполнить с помощью list comprehension: [round(math.hypot(a, b), 2) for a, b in pairs], где pairs – список кортежей со сторонами прямоугольного треугольника.
Обработка ошибок при вводе некорректных данных

Для предотвращения сбоев при вычислении гипотенузы необходимо учитывать возможность ввода пользователем некорректных значений. Это включает пустые строки, текст вместо чисел, отрицательные значения и ноль.
Рекомендуется использовать конструкцию try-except с предварительной проверкой на положительность значений. Пример реализации:
try:
a = float(input("Введите длину первого катета: "))
b = float(input("Введите длину второго катета: "))
if a <= 0 or b <= 0:
raise ValueError("Катеты должны быть положительными числами")
except ValueError as e:
print("Ошибка:", e)
else:
from math import sqrt
c = sqrt(a2 + b2)
print("Гипотенуза:", c)
В данном примере ввод обрабатывается строго: float() преобразует данные, и при передаче строки, содержащей нечисловые символы, срабатывает исключение ValueError. Дополнительно вручную вызывается исключение при отрицательных или нулевых значениях.
Такой подход позволяет исключить невалидные данные до начала вычислений и предотвратить логические ошибки в программе.
Создание функции для многократного использования расчёта
Для упрощения процесса вычисления гипотенузы можно создать функцию, которая будет принимать длины катетов и возвращать результат. В Python это можно сделать с использованием стандартной библиотеки math, которая содержит функцию sqrt() для вычисления квадратного корня.
Функция, рассчитывающая гипотенузу, должна быть универсальной и работать с любыми значениями длины катетов. Рассмотрим пример кода:
import math
def calculate_hypotenuse(a, b):
return math.sqrt(a2 + b2)Эта функция принимает два параметра: a и b, которые соответствуют длинам катетов. Внутри функции вычисляется сумма квадратов катетов, и затем берётся квадратный корень от этой суммы, что и является длиной гипотенузы.
Пример использования функции:
cathetus_a = 3
cathetus_b = 4
hypotenuse = calculate_hypotenuse(cathetus_a, cathetus_b)
print(f'Гипотенуза: {hypotenuse}') # Результат: 5.0Такой подход позволяет избежать повторения кода при многократных расчётах и упрощает тестирование и использование функции. Кроме того, эту функцию можно расширить, добавив обработку ошибок, чтобы учитывать случаи, когда введённые значения не являются положительными числами.
Пример улучшенной версии с проверкой данных:
def calculate_hypotenuse(a, b):
if a <= 0 or b <= 0:
raise ValueError("Длины катетов должны быть положительными числами.")
return math.sqrt(a2 + b2)Теперь функция будет выбрасывать ошибку, если значения катетов не соответствуют условиям задачи. Это повышает её надёжность при использовании в различных сценариях.
Вопрос-ответ:
Почему для вычисления гипотенузы используется функция `math.sqrt`?
Функция `math.sqrt` в Python используется для извлечения квадратного корня. Это необходимо, потому что для нахождения гипотенузы по теореме Пифагора нужно извлечь квадратный корень из суммы квадратов катетов. Формула для гипотенузы выглядит так: \( c = \sqrt{a^2 + b^2} \), где \(a\) и \(b\) — катеты, а \(c\) — гипотенуза. В Python для извлечения квадратного корня и выполнения математических операций используется библиотека `math`.