Как найти корень числа в python

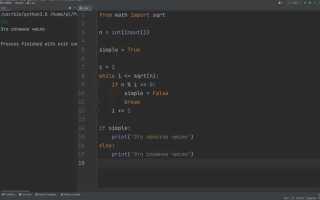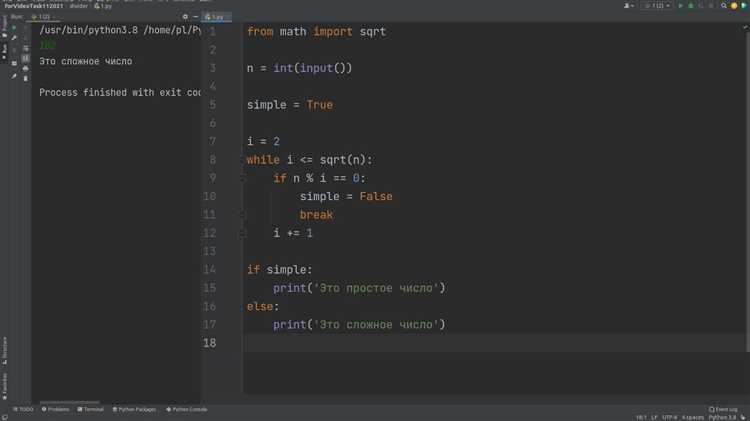
Работа с корнями чисел – одна из базовых операций в вычислениях, и Python предлагает несколько способов её реализации. В стандартной библиотеке доступен модуль math, в котором функция math.sqrt(x) возвращает квадратный корень числа x. Однако это решение ограничено только действительными неотрицательными числами и не поддерживает вычисление корней других степеней или комплексных значений.

Для более гибкой работы с корнями, включая извлечение корней произвольной степени, Python позволяет использовать оператор возведения в степень: x (1/n), где n – степень корня. Такой подход обеспечивает универсальность и подходит как для положительных, так и для отрицательных чисел, если использовать модуль cmath для комплексных значений.

В задачах, связанных с обработкой больших массивов чисел или высокоточными вычислениями, предпочтительно использовать библиотеку NumPy. Функция numpy.power и универсальное возведение в степень через array (1/n) эффективно работают с векторами и матрицами, предоставляя точный и быстрый результат даже при больших объёмах данных.

Важно учитывать тип данных: извлечение корня из отрицательного числа без использования комплексной арифметики вызовет ValueError. Для комплексных чисел необходимо использовать cmath.sqrt или оператор с модулем cmath. Пренебрежение этим правилом приведёт к сбоям в выполнении кода.

• Для любого положительного числа x, квадратный корень вычисляется как x 0.5.
• Пример: result = 25 0.5 вернёт 5.0.
• Оператор работает с типами int и float, результат всегда float.
• Отрицательные значения вызовут ошибку ValueError, если применить 0.5 напрямую.

Рекомендации по использованию:

1. Проверяйте входные значения: if x >= 0, чтобы избежать ошибок.
2. Используйте abs(x) 0.5 только при математической уверенности в корректности результата.
3. Для работы с комплексными корнями используйте cmath.sqrt(x).

Важно: math.pow() работает с числами с плавающей точкой и может давать погрешности. Для повышения точности используйте a (1/n), особенно при работе с целыми корнями. Например: 125 (1/3) возвращает 5.0.

import cmath
result = cmath.sqrt(-25)

import math
def safe_sqrt(x):
if x < 0:
return None
return math.sqrt(x)

import math
import cmath
def unified_sqrt(x):
return math.sqrt(x) if x >= 0 else cmath.sqrt(x)

import cmath
x = -16
root = cmath.sqrt(x)
print(root)

z = (-16)  0.5
print(z)

Этот код также вернет комплексное число, соответствующее корню из -16.

Как реализовать собственную функцию извлечения корня без сторонних библиотек

Для извлечения квадратного корня числа можно использовать алгоритм Ньютона (или метод Ньютона-Рапсона). Этот метод позволяет вычислить корень числа с высокой точностью и без использования сторонних библиотек. Он основан на итеративном подходе, который постепенно приближает значение к реальному корню.

Основная идея заключается в том, чтобы для числа n и текущего приближения x использовать следующую формулу для нового приближения:

xn+1 = 0.5 * (xn + n / xn)

Где xn – это текущая аппроксимация, а xn+1 – новое приближение, которое будет более точным. Процесс повторяется до тех пор, пока разница между текущим и следующим приближением не станет достаточно маленькой (например, менее заданной точности).

Пример реализации функции для нахождения квадратного корня:

def sqrt(n, epsilon=1e-10):
if n < 0:
raise ValueError("Не существует квадратного корня для отрицательного числа.")
if n == 0:
return 0
x = n
while True:
x_new = 0.5 * (x + n / x)
if abs(x - x_new) < epsilon:
break
x = x_new
return x

В этом коде:

• n – число, для которого ищется корень;
• epsilon – точность вычислений (по умолчанию 1e-10);
• Алгоритм будет продолжать итерации, пока разница между соседними значениями не станет меньше epsilon.

Такой подход позволяет эффективно находить корни, обеспечивая высокую точность при относительно небольших вычислительных затратах. Преимущества метода Ньютона заключаются в его быстром сходимости, особенно для больших чисел. Однако следует учитывать, что метод требует начального приближения, которое должно быть достаточно близким к реальному корню, чтобы избежать сходимости к неправильным значениям при вычислениях.

Сравнение точности разных методов нахождения корня в Python

В Python существует несколько методов нахождения корня числа, каждый из которых имеет свои особенности точности и производительности. Рассмотрим основные из них и их поведение на примерах.

1. Использование оператора `` (возведение в степень)

sqrt_x = x 0.5

print(sqrt_x)

Результат: 4.0

2. Использование функции `math.sqrt()`

Функция `math.sqrt()` является частью стандартной библиотеки Python и предназначена для вычисления квадратного корня. Она обычно точнее, чем оператор ``, поскольку реализует более точные алгоритмы и работает с типом данных, который оптимизирован для математических операций. Однако, как и в предыдущем методе, она может давать погрешности для чисел с плавающей точкой, особенно если они очень велики или малы.

3. Использование метода Ньютона (или метода касательных)**

Метод Ньютона, также известный как метод касательных, является итерационным методом для нахождения корней. Он может быть использован для вычисления квадратного корня числа. Этот метод часто дает точность, превосходящую стандартные методы при достаточном числе итераций, однако его скорость и точность зависят от начального приближения. Неправильное приближение может привести к ошибкам.

Пример:

```python

def sqrt_newton(x):

guess = x / 2.0

while abs(guess * guess - x) > 1e-10:

guess = (guess + x / guess) / 2.0

return guess

x = 16

sqrt_x = sqrt_newton(x)

print(sqrt_x)

pgsqlEditРезультат: 4.0

4. Использование библиотеки `decimal` для точных вычислений

Библиотека `decimal` позволяет вычислять квадратный корень с произвольной точностью, что полезно при работе с числами, требующими высокой точности, например, в финансовых расчетах. Она значительно более точна, чем стандартные методы для чисел с плавающей точкой, и подходит для случаев, когда требуется большее количество знаков после запятой.

Пример:

```python

from decimal import Decimal, getcontext

getcontext().prec = 50

x = Decimal(16)

sqrt_x = x.sqrt()

print(sqrt_x)

Результат: 4.0

5. Использование библиотеки `numpy` для работы с массивами

Для работы с массивами чисел библиотека `numpy` предоставляет функцию `numpy.sqrt()`, которая оптимизирована для массовых вычислений. Хотя эта функция работает быстро и точно для массивов, она использует стандартные типы данных с плавающей точкой, поэтому для отдельных значений может быть менее точной, чем другие методы, такие как `math.sqrt()` или `decimal.sqrt()`.

Пример:

```python

import numpy as np

x = np.array([16, 25, 36])

sqrt_x = np.sqrt(x)

print(sqrt_x)

Результат: [4. 5. 6.]

Вопрос-ответ: