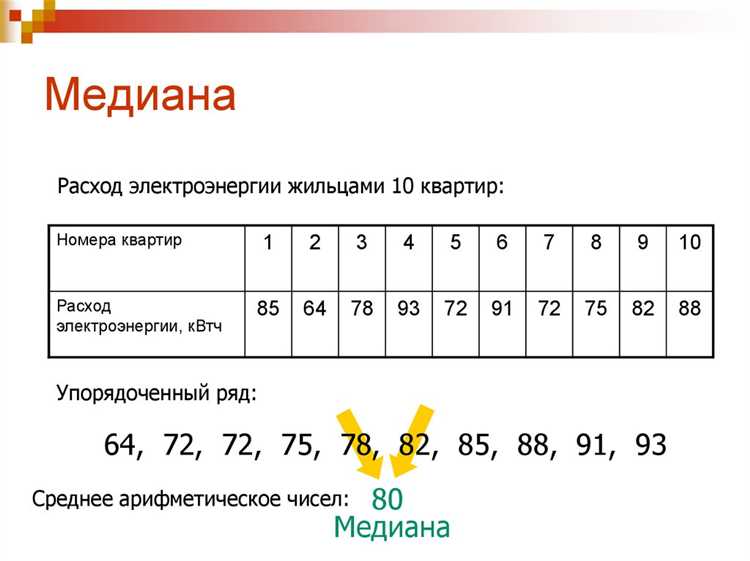
Медиана – это центральное значение в упорядоченном наборе данных. Она делит данные на две равные части, где половина элементов меньше медианы, а другая половина больше. В Python вычисление медианы можно выполнить несколькими способами, используя встроенные функции или библиотеки, такие как numpy и statistics.
Если нужно вычислить медиану без использования сторонних библиотек, можно воспользоваться стандартными средствами языка. Для этого нужно отсортировать список данных и затем найти центральное значение. Важно учитывать, что медиана для четного количества элементов будет вычисляться как среднее значение двух центральных чисел. Например, для списка [1, 3, 5, 7], медианой будет (3+5)/2 = 4.
Пример:
data = [1, 3, 5, 7]
data.sort()
if len(data) % 2 == 0:
median = (data[len(data)//2 - 1] + data[len(data)//2]) / 2
else:
median = data[len(data)//2]
Для упрощения вычислений можно воспользоваться функцией median() из библиотеки statistics, которая делает все вычисления автоматически. Этот метод идеально подходит для большинства задач и особенно полезен при работе с большими наборами данных.
Пример с использованием statistics:
import statistics
data = [1, 3, 5, 7]
median = statistics.median(data)
Если требуется работать с массивами чисел в научных расчетах, лучше использовать numpy, так как она предоставляет более быстрые и эффективные методы. В случае с большими объемами данных вычисление медианы с помощью numpy будет гораздо быстрее по сравнению с простыми сортировками.
Пример с использованием numpy:
import numpy as np
data = [1, 3, 5, 7]
median = np.median(data)
Использование библиотеки NumPy для вычисления медианы

Библиотека NumPy предоставляет эффективный способ вычисления медианы с помощью функции numpy.median(). Эта функция позволяет быстро обрабатывать большие массивы данных, что особенно важно при работе с научными вычислениями и анализом данных. Медиану можно вычислить как для одномерных массивов, так и для многомерных, с дополнительной возможностью указания оси для вычислений по строкам или столбцам.
Для вычисления медианы одномерного массива достаточно передать его в функцию numpy.median(). Например:
import numpy as np
data = [1, 3, 5, 7, 9]
median_value = np.median(data)
print(median_value)Этот код выведет медиану набора данных, которая равна 5, так как это среднее значение в отсортированном наборе {1, 3, 5, 7, 9}.
В случае с многомерными массивами можно указать ось, по которой будет вычисляться медиана. Например, для вычисления медианы по строкам или столбцам в двумерном массиве:
data_2d = np.array([[1, 3, 5], [7, 9, 11], [13, 15, 17]])
median_rows = np.median(data_2d, axis=1) # Медиана по строкам
median_columns = np.median(data_2d, axis=0) # Медиана по столбцам
print(median_rows)
print(median_columns)Результат работы кода будет следующим:
[3. 9. 15.]Это медианы по строкам, а также:
[7. 9. 11.]Для вычисления медианы по столбцам. Параметр axis позволяет гибко выбирать ось, что значительно упрощает работу с многомерными массивами.
В случае с четным числом элементов в массиве, NumPy возвращает медиану как среднее значение двух центральных элементов. Например:
data = [1, 3, 5, 7]
median_value = np.median(data)
print(median_value)Результат будет равен 4, так как среднее значение между 3 и 5 – это 4.
Вычисление медианы с помощью стандартной библиотеки Python
Для вычисления медианы в Python достаточно использовать модуль statistics, который входит в стандартную библиотеку. Этот модуль содержит функцию median(), позволяющую быстро находить медиану набора чисел.
Пример использования функции median():
import statistics
data = [1, 3, 3, 6, 7, 8, 9]
result = statistics.median(data)
print(result) # Выведет 6Функция median() автоматически сортирует список и находит центральное значение. В случае четного числа элементов медиана будет вычислена как среднее значение двух центральных элементов.
Пример с четным количеством чисел:
data = [1, 2, 3, 4]
result = statistics.median(data)
print(result) # Выведет 2.5- Если список содержит одинаковые элементы, медианой будет это значение.
- Функция работает как с целыми числами, так и с числами с плавающей запятой.
Важно помнить, что метод median() не изменяет исходный список и не требует дополнительной обработки для стандартных случаев. Однако, если необходимо работать с большими данными или учитывать особенности данных (например, пропуски), можно использовать дополнительные библиотеки, такие как numpy.
Если нужно вычислить медиану для неупорядоченных данных, то стандартная функция все равно выполнит сортировку, что делает ее эффективным и быстрым решением для большинства задач.
Как найти медиану для списка с нечетным количеством элементов
Для поиска медианы в списке с нечетным количеством элементов нужно отсортировать этот список, а затем выбрать центральный элемент. Порядок действий следующий:
1. Сортируйте список элементов по возрастанию.
2. Найдите индекс центрального элемента. Для списка из N элементов индекс медианы будет равен (N // 2).
3. Верните элемент на этом индексе, который и будет медианой.
Пример:
список = [7, 2, 9, 4, 1] список.sort() медиана = список[len(список) // 2]
После сортировки список будет выглядеть так: [1, 2, 4, 7, 9]. Индекс медианы – 2, и медианой является число 4.
Важное замечание: для списка с нечетным количеством элементов медиана всегда будет одним числом, а не средним значением двух элементов, как это бывает в списках с четным количеством элементов.
Как найти медиану для списка с четным количеством элементов
Для вычисления медианы списка с четным количеством элементов нужно сначала отсортировать его. Медианой считается среднее значение двух центральных элементов после сортировки.
Допустим, у вас есть список из 6 элементов: [3, 1, 4, 2, 5, 6]. После сортировки он выглядит так: [1, 2, 3, 4, 5, 6].
Чтобы найти медиану, нужно взять два центральных элемента. В данном примере это 3 и 4 (они находятся на позициях 2 и 3, начиная с нуля). Медиана будет равна среднему значению этих чисел:
Медиана = (3 + 4) / 2 = 3.5
Для реализации этого в Python можно использовать такой код:
def find_median(lst):
lst.sort()
n = len(lst)
if n % 2 == 0:
return (lst[n//2 - 1] + lst[n//2]) / 2
else:
return lst[n//2]
Функция сначала сортирует список, затем проверяет его длину. Если количество элементов четное, возвращается среднее значение двух центральных элементов. В случае нечетного количества элементов возвращается один центральный элемент.
Вычисление медианы для многомерных массивов в Python
В Python для работы с многомерными массивами удобно использовать библиотеку NumPy, которая предоставляет функции для быстрого и эффективного вычисления медианы.
Медиана – это значение, которое разделяет массив на две равные части. В случае многомерных массивов, вычисление медианы может быть выполнено вдоль определённой оси.
Для вычисления медианы для многомерного массива можно использовать функцию numpy.median(), которая позволяет работать с массивами любой размерности. При этом, медиана может быть вычислена как по всем данным массива, так и вдоль заданной оси.
Основной пример
Допустим, у нас есть двумерный массив:
import numpy as np
arr = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
median = np.median(arr)
print(median) # Выведет медиану по всем данным
Результатом будет медиана всех элементов массива, независимо от их расположения.
Вычисление медианы вдоль оси
Для вычисления медианы вдоль оси можно указать параметр axis:
# Медиана по строкам (axis=1)
median_rows = np.median(arr, axis=1)
print(median_rows) # Выведет медиану для каждой строки
# Медиана по столбцам (axis=0)
median_columns = np.median(arr, axis=0)
print(median_columns) # Выведет медиану для каждого столбца
Если axis=0, медиана будет вычислена по каждому столбцу, а если axis=1, то по каждой строке.
Работа с массивами более высокой размерности
Для многомерных массивов размерности больше двух, работа с осью остаётся аналогичной:
arr_3d = np.random.randint(1, 10, size=(2, 3, 4)) # Трехмерный массив
median_3d = np.median(arr_3d, axis=2)
print(median_3d) # Медиана по последней оси
Здесь axis=2 обозначает ось вдоль глубины (по третьему измерению). Можно выбрать любую ось в зависимости от задачи.
Особенности
- Медиана для чётных массивов берётся как среднее значение двух центральных элементов.
- Медиана работает только с числовыми данными. Для других типов данных требуется их предварительная конвертация.
- Если данные содержат NaN, медиана будет вычислена только для ненулевых значений, если не указано иначе (параметр
nan_policy).
Как обработать данные с пропущенными значениями при вычислении медианы
При работе с данными часто встречаются пропущенные значения, что может повлиять на точность расчётов, в том числе при вычислении медианы. В Python для обработки таких данных существует несколько подходов.
1. Игнорирование пропущенных значений
Один из простых способов – исключить пропущенные значения из набора данных перед вычислением медианы. В Python для этого можно использовать метод dropna() библиотеки pandas. Этот подход подходит, когда количество пропусков минимально, и их удаление не повлияет на результаты анализа.
Пример кода:
import pandas as pd data = pd.Series([1, 2, None, 4, 5]) cleaned_data = data.dropna() median = cleaned_data.median()
2. Заполнение пропущенных значений
Заполнение пропусков подходяще значением, которое не искажает распределение данных, – другой метод обработки. Обычно для этого используется среднее, медианное или модальное значение. Заполнение медианой полезно, так как оно не влияет на общий порядок значений.
Пример кода для заполнения медианой:
data_filled = data.fillna(data.median()) median_filled = data_filled.median()
3. Использование специальных функций в библиотеке numpy
Если данные представлены в виде массива или списка, то можно воспользоваться функцией numpy.nanmedian(), которая автоматически игнорирует пропущенные значения при вычислении медианы. Это решение избавляет от необходимости предварительной очистки данных или заполнения пропусков.
Пример кода:
import numpy as np data = [1, 2, np.nan, 4, 5] median = np.nanmedian(data)
4. Методы для анализа больших данных
В случае работы с большими наборами данных, где пропуски могут встречаться чаще, чем в малых, имеет смысл применять более сложные методы, такие как интерполяция или моделирование пропущенных значений с использованием статистических методов. В этом случае для вычисления медианы рекомендуется использовать продвинутые функции библиотеки statsmodels или sklearn, которые предлагают методы для восстановления пропусков на основе других наблюдений.
Вопрос-ответ:
Что делать, если данные содержат повторяющиеся значения? Влияет ли это на вычисление медианы?
Повторяющиеся значения не влияют на вычисление медианы. Медиана определяется просто как центральное значение в отсортированном списке. Если повторяющиеся значения находятся рядом, они будут учтены в сортировке. Например, для списка `[1, 2, 2, 3, 5]` медианой будет 2, так как она стоит в центре. Даже если 2 встречается несколько раз, она всё равно остаётся медианой, так как занимает центральное место в отсортированном списке.