Как найти сумму чисел в числе python

Для решения задачи нахождения суммы цифр числа на Python существует несколько подходов, в зависимости от целей и предпочтений разработчика. Задача требует не только знания синтаксиса, но и умения эффективно работать с числами и строками. В большинстве случаев можно воспользоваться базовыми средствами языка, такими как операторы деления и остатка, или же перейти к более сложным методам, используя возможности встроенных функций.

Один из самых простых способов – это разделить число на цифры с помощью оператора деления и остатка от деления. Это позволяет извлечь каждую цифру числа, начиная с последней, и затем суммировать их. Однако такой подход требует внимательности при работе с большими числами, так как может потребоваться большое количество итераций.

Другой способ – преобразовать число в строку, разделить её на символы и затем преобразовать каждый символ обратно в цифру для суммирования. Этот метод считается более читаемым и часто используется в задачах, где важна простота и ясность кода.

Каждый из этих методов имеет свои преимущества, и выбор зависит от конкретной задачи. Например, использование арифметических операций может быть полезно при работе с большими числами, где важно минимизировать использование памяти. В то время как подход с преобразованием числа в строку подходит для небольших чисел или когда удобство кода важнее производительности.

Использование цикла для нахождения суммы цифр

Пример кода на Python:

def sum_digits(number):
total = 0
while number > 0:
total += number % 10
number //= 10
return total

В этом примере используется цикл while, который выполняется до тех пор, пока число не станет равным нулю. На каждом шаге из числа извлекается последняя цифра с помощью операции % 10 (остаток от деления на 10), и эта цифра добавляется к общей сумме. Затем число сокращается с помощью операции целочисленного деления // 10, удаляя последнюю цифру.

Этот метод работает корректно для целых положительных чисел. Если число отрицательное, его можно привести к положительному значению с помощью функции abs().

Использование цикла для нахождения суммы цифр эффективно, так как позволяет работать с числом любой длины, а алгоритм имеет линейную сложность – время работы растет пропорционально количеству цифр в числе.

Как решить задачу с помощью функции sum() и генератора списков

Для нахождения суммы цифр числа можно эффективно использовать функцию sum() в сочетании с генератором списков. Этот метод позволяет компактно и быстро решать задачу, избавляя от необходимости вручную обрабатывать каждую цифру числа.

Алгоритм заключается в следующем: необходимо преобразовать число в строку, затем с помощью генератора списков извлечь каждую цифру, привести её к числовому типу и вычислить сумму всех полученных чисел.

Пример кода для нахождения суммы цифр числа:

number = 12345
sum_of_digits = sum(int(digit) for digit in str(number))
print(sum_of_digits)

В этом примере:

str(number) преобразует число в строку, чтобы получить доступ к каждой цифре.
Генератор int(digit) for digit in str(number) итерирует по каждому символу строки и превращает его в целое число.
Функция sum() вычисляет сумму всех чисел, полученных из цифр.

Такой подход позволяет решить задачу за одну строку кода, при этом решение остаётся понятным и легко модифицируемым.

Использование генераторов списков в сочетании с sum() существенно сокращает время выполнения программы, поскольку эти конструкции оптимизированы для работы с большими объёмами данных.

Обработка отрицательных чисел при вычислении суммы цифр

При вычислении суммы цифр в числе важно учесть, что отрицательные числа имеют минус, который не влияет на сами цифры. Для корректной обработки отрицательных чисел можно использовать встроенные функции Python, такие как abs(), чтобы игнорировать знак числа и работать только с его абсолютной величиной.

Пример кода:

number = -12345
sum_digits = sum(int(digit) for digit in str(abs(number)))
print(sum_digits)

В данном примере функция abs() удаляет минус перед числом, и далее производится вычисление суммы цифр числа с использованием генератора списка и функции sum().

Обратите внимание, что использование abs() гарантирует, что знак числа не повлияет на вычисления, и программа будет работать корректно независимо от того, положительное число или отрицательное передано в качестве аргумента.

Важно: если задача требует учета знака числа (например, для вычисления какого-либо специализированного результата), то обработку знака следует выполнять отдельно от подсчета суммы цифр. В противном случае, использование abs() – лучший способ обеспечить точность работы программы при обработке отрицательных чисел.

Применение рекурсии для нахождения суммы цифр

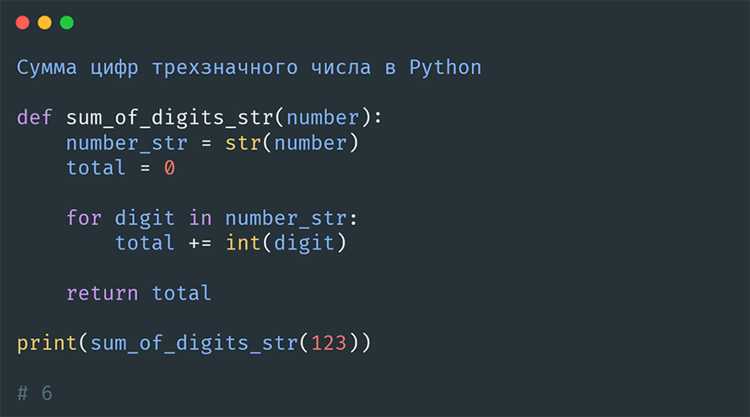
Рекурсивный подход для нахождения суммы цифр числа заключается в следующем: на каждом шаге функция делит число на его последнюю цифру и остаток, вызывая себя для оставшейся части числа. Как только число становится равным 0, рекурсия завершится, и результат будет равен сумме цифр.

Пример рекурсивной функции для вычисления суммы цифр выглядит следующим образом:

def sum_of_digits(n):
if n == 0:
return 0
return n % 10 + sum_of_digits(n // 10)

Здесь условие `if n == 0:` является базовым случаем, при котором рекурсия прекращается. Если число не равно 0, то выполняется операция нахождения последней цифры числа через остаток от деления на 10 (`n % 10`), а затем рекурсивный вызов для числа, которое получается после удаления последней цифры (`n // 10`).

Такой подход позволяет легко и понятно решить задачу, при этом код остаётся компактным. Однако стоит помнить, что рекурсия может привести к переполнению стека вызовов при очень больших числах, так как каждый новый вызов функции добавляется в стек. Поэтому при работе с большими числами стоит использовать итеративные методы или увеличивать лимит рекурсии в Python.

Рекурсивный способ нахождения суммы цифр идеально подходит для образовательных целей и для задач, где важна наглядность и краткость решения. В реальных приложениях, если числа очень большие, лучше использовать другие алгоритмы, чтобы избежать излишней нагрузки на память.

Преобразование числа в строку для упрощения решения задачи

Чтобы найти сумму цифр числа, его можно преобразовать в строку. Это делает задачу проще, так как мы можем работать с каждой цифрой по отдельности, обходя число символ за символом.

Преобразование числа в строку в Python выполняется с помощью функции str(). Например, если у нас есть число 123, после применения str(123) мы получим строку "123".

Преимущества такого подхода заключаются в том, что строки легко итерировать с помощью циклов. Мы можем пройти по каждому символу строки и преобразовать его обратно в число с помощью int(), чтобы вычислить сумму цифр.

Вот пример кода, который демонстрирует этот подход:

number = 123
number_str = str(number)
sum_digits = sum(int(digit) for digit in number_str)
print(sum_digits)  # Выведет 6

Таким образом, преобразование числа в строку упрощает задачу за счет упрощения итерации по цифрам и позволяет использовать стандартные функции Python для работы с цифрами в виде строк.

Оптимизация кода для работы с большими числами

При обработке больших чисел важно учитывать эффективность кода, чтобы избежать задержек и лишней нагрузки на ресурсы. Вот несколько рекомендаций для оптимизации выполнения операций с большими числами на Python:

Использование строкового представления числа: При работе с большими числами можно воспользоваться строкой, так как доступ к символам строки и их обработка может быть быстрее, чем манипуляции с самими числами. Для подсчета суммы цифр можно пройти по строковому представлению числа, преобразуя каждый символ в цифру.
Применение встроенных функций: Использование встроенных функций, таких как sum и map, может значительно ускорить процесс. Эти функции реализованы на C и оптимизированы для работы с большими объемами данных.
Минимизация использования циклов: Обычные циклы могут замедлять работу при больших числах. Вместо этого, используйте рекурсивные решения или обработку данных в виде списков с использованием функций высшего порядка, таких как reduce.
Избегание повторных преобразований: Если число уже преобразовано в строку, избегайте повторного преобразования его обратно в целое число. Работа с строками и их индексация может быть более эффективной в таких случаях.
Использование генераторов: Генераторы позволяют экономить память и ускорять выполнение за счет ленивой обработки элементов. Вместо создания полного списка цифр числа можно использовать генератор, который будет работать с каждым символом поочередно.

Пример оптимизированного кода для подсчета суммы цифр большого числа:


def sum_of_digits(n):
return sum(map(int, str(n)))

Этот код быстро работает, даже если число состоит из миллионов цифр, за счет использования эффективных встроенных методов и минимизации работы с промежуточными данными.