Для эффективного поиска делителей числа в Python существует несколько подходов, которые могут быть полезны в различных ситуациях. Знание этих методов позволяет выбрать оптимальное решение в зависимости от конкретных задач. Например, для небольших чисел подойдет простое переборное решение, в то время как для больших чисел могут быть полезны более сложные алгоритмы с улучшенной производительностью.
Основная идея поиска делителей заключается в том, чтобы для каждого числа от 1 до заданного числа проверить, делится ли оно на это число без остатка. Однако, этот метод требует времени, пропорционального величине самого числа, что может быть неэффективно при работе с большими значениями.
Для оптимизации этого процесса стоит учитывать, что делители числа всегда приходят парами. Например, если число 36 делится на 2, то оно также делится и на 18. Это позволяет сократить количество проверок до корня из числа, что значительно повышает скорость алгоритма. Такой подход является не только эффективным, но и легко реализуемым на Python, обеспечивая нужную производительность при работе с большими числами.
Алгоритм поиска делителей с использованием цикла
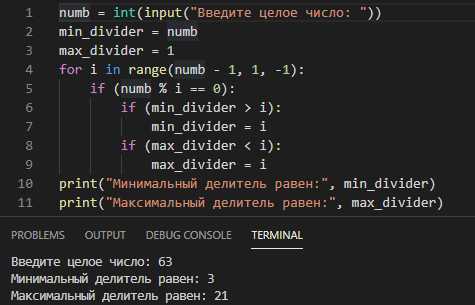
Основная идея алгоритма – проверить, делится ли заданное число на другие числа без остатка. Если остаток от деления равен нулю, значит, текущее число – делитель. В цикле достаточно проходить только до половины числа, так как все делители больше этой величины уже будут найденными в предыдущих шагах.
Рассмотрим пример алгоритма на Python:
def find_divisors(n): divisors = [] for i in range(1, n//2 + 1): if n % i == 0: divisors.append(i) divisors.append(n) # само число тоже делится на себя return divisors number = 36 print(find_divisors(number))
В этом примере цикл проходит от 1 до половины числа, проверяя, делится ли текущее число на переданное. Если делитель найден, он добавляется в список. В конце добавляется само число, так как оно всегда делится на себя.
Такой алгоритм эффективен для небольших чисел. Для больших чисел, если важно ускорить поиск, можно использовать более сложные методы, но для большинства случаев подход с циклом будет достаточен.
Как ускорить поиск делителей с помощью перебора до квадратного корня
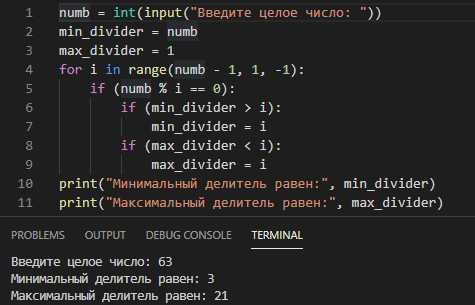
При поиске делителей числа простым перебором каждый делитель проверяется на целочисленное деление от 1 до самого числа. Однако можно существенно ускорить этот процесс, ограничив диапазон поиска до квадратного корня из числа.
Делители числа идут парами. Например, если число делится на какое-то значение a, то вторым делителем будет число b, равное числу, которое получается при делении исходного числа на a: b = n / a. Пары делителей симметричны относительно квадратного корня из числа. Это означает, что достаточно искать делители только до квадратного корня числа, а для каждого найденного делителя автоматически вычислять второй.
Рассмотрим на примере алгоритм поиска делителей с использованием этого подхода:
- Вычислить квадратный корень числа n.
- Пройтись по всем числам от 1 до квадратного корня из n (включительно).
- Для каждого числа a, если n делится на a без остатка, то a и n / a – делители числа.
- При нахождении делителя, если a != n / a, добавить оба делителя.
Этот метод сокращает количество проверок, особенно для больших чисел, поскольку диапазон для перебора значительно меньше.
Пример кода на Python:
import math def find_divisors(n): divisors = set() for i in range(1, int(math.sqrt(n)) + 1): if n % i == 0: divisors.add(i) divisors.add(n // i) return sorted(divisors) print(find_divisors(36))
В данном примере для числа 36 проверяются только числа от 1 до 6, а для каждого найденного делителя вычисляется и второй делитель. Это позволяет существенно ускорить выполнение программы по сравнению с полным перебором всех чисел до 36.
Для чисел, у которых есть много делителей, этот метод экономит не только время, но и память, поскольку число проверок значительно сокращается.
Реализация функции для поиска всех делителей числа

Для нахождения всех делителей числа в Python можно воспользоваться простым методом, который позволяет эффективно пройти по числам от 1 до квадратного корня из числа. Такой подход сокращает количество операций, так как делители числа всегда идут парами, и для чисел больших квадратного корня можно сразу найти соответствующие меньшие делители.
Основная идея алгоритма заключается в том, чтобы проверить, делится ли число на все числа от 1 до его квадратного корня. Если делится, то добавляем в список не только делитель, но и его пару, делённую на исходное число. Это позволяет сразу получить два делителя за одну операцию.
Пример реализации функции:
def find_divisors(n): divisors = [] for i in range(1, int(n 0.5) + 1): if n % i == 0: divisors.append(i) if i != n // i: # Чтобы избежать повторения квадратного корня divisors.append(n // i) return sorted(divisors)
Функция find_divisors принимает на вход целое число n и возвращает список всех его делителей, отсортированных в порядке возрастания. В цикле мы проверяем числа от 1 до sqrt(n). Если число делит n, добавляем его в список, а также добавляем пару, полученную делением n на это число, если она отличается от самого числа.
Пример использования функции:
n = 36
Этот метод позволяет эффективно находить все делители чисел, минимизируя количество проверок и повышая производительность. Алгоритм работает за время порядка O(√n), что значительно быстрее, чем проверка всех чисел от 1 до n.
Поиск делителей с использованием списка и множества
Для поиска делителей числа с использованием Python можно применить два популярных подхода: использование списка и использование множества. Каждый метод имеет свои особенности, преимущества и недостатки.
Сначала рассмотрим использование списка. Список в Python – это упорядоченная коллекция элементов. При поиске делителей мы проходим от 1 до числа и проверяем, делится ли текущее число на рассматриваемое. Если делится, добавляем его в список.
def find_divisors_list(n): divisors = [] for i in range(1, n+1): if n % i == 0: divisors.append(i) return divisors
Этот метод работает корректно, но есть один момент: список может содержать повторяющиеся значения, если, например, число является квадратом. Тем не менее, в случае с небольшими числами, это решение является простым и понятным.
Теперь рассмотрим использование множества. Множество в Python – это неупорядоченная коллекция уникальных элементов. Преимущество множества заключается в том, что оно автоматически удаляет повторяющиеся элементы, что делает его более эффективным для поиска делителей числа, особенно если число большое.
def find_divisors_set(n): divisors = set() for i in range(1, n+1): if n % i == 0: divisors.add(i) return divisors
Метод с множеством особенно полезен, если необходимо получить только уникальные делители, без дублирования. Однако стоит отметить, что в отличие от списка, множество не сохраняет порядок добавления элементов.
Выбор между списком и множеством зависит от задачи. Если порядок делителей имеет значение или вам важно сохранить их последовательность, лучше использовать список. В случае, когда важна только уникальность делителей и производительность, оптимальным выбором будет множество.
Как найти все делители числа для больших значений
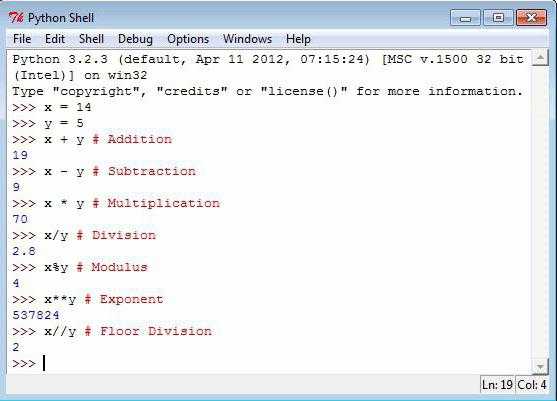
Для числа N, чтобы найти все его делители, достаточно пройти по числам от 1 до √N. Если N делится на число i, то i и N/i будут делителями. Это значительно сокращает количество проверок, так как после √N можно получить пары делителей, используя их взаимную связь. Например, для числа 36 мы проверяем делимость до 6 (√36), и находим пары: (1, 36), (2, 18), (3, 12), (4, 9), (6, 6).
Пример кода на Python для нахождения делителей числа:
def find_divisors(n): divisors = set() for i in range(1, int(n0.5) + 1): if n % i == 0: divisors.add(i) divisors.add(n // i) return sorted(divisors)
Этот метод уменьшает количество операций с O(N) до O(√N), что особенно важно для очень больших чисел.
Однако для еще более эффективного поиска делителей при работе с большими числами можно использовать алгоритмы числового разложения, такие как метод «решета Эратосфена», чтобы исключить уже найденные простые числа и их кратные. Это позволяет ускорить процесс нахождения делителей для чисел с большим количеством факторов.
Для еще большего ускорения можно использовать многозадачность или параллельные вычисления, если число очень велико и стандартные методы уже начинают требовать значительных временных ресурсов. Но для большинства случаев использование метода через √N будет достаточно быстрым и оптимальным решением.
Обработка ошибок и проверка на ввод неверных данных

При написании программы для поиска делителей числа важно учитывать возможность ввода неверных данных. Если пользователь введет строку вместо числа или отрицательное значение, программа может завершиться с ошибкой. Поэтому необходимо заранее предусмотреть такие ситуации и обработать их.
try:
number = int(input("Введите число: "))
except ValueError:
print("Ошибка: введено нецелое число.")
Этот код обработает ошибку, если пользователь введет нечисловое значение. Однако, чтобы избежать деления на ноль или работы с отрицательными числами, можно добавить дополнительные проверки. Например, для проверки на ноль или отрицательные значения можно использовать условие:
if number <= 0:
print("Ошибка: число должно быть больше нуля.")
Такой подход предотвращает попытки вычислений с неподобающими числами и помогает избежать логических ошибок в программе.
Для более сложных сценариев можно использовать цикл, который будет запрашивать ввод до тех пор, пока не будет введено корректное значение. Это можно реализовать с помощью while:
while True:
try:
number = int(input("Введите положительное число: "))
if number <= 0:
print("Ошибка: число должно быть больше нуля.")
else:
break
except ValueError:
print("Ошибка: введено нецелое число.")
Такой цикл продолжит запрашивать ввод, пока пользователь не введет правильное положительное целое число.
Еще одним важным аспектом является проверка, не является ли введенное число слишком большим для обработки. В Python нет строгих ограничений на размер целых чисел, но в некоторых случаях имеет смысл проверять их диапазон, чтобы избежать чрезмерных вычислительных затрат или ошибок памяти.
Проверка на границы значений позволяет сделать программу более устойчивой и избежать неожиданных ситуаций. Таким образом, тщательная обработка ошибок и проверка ввода – важные шаги для создания надежной программы для поиска делителей числа.