Как написать генератор случайных чисел на python

В стандартной библиотеке Python модуль random предоставляет функции для генерации случайных чисел, однако его поведение основано на алгоритмах псевдослучайности, таких как Mersenne Twister. Чтобы глубже понять принципы работы генераторов, полезно реализовать собственный механизм с нуля, не полагаясь на внешние зависимости.

Один из простейших подходов – линейный конгруэнтный метод. Он описывается формулой: X_n+1 = (aX_n + c) mod m, где параметры a, c и m подбираются так, чтобы обеспечить приемлемую длину периода и равномерность распределения. Начальное значение X₀ – это зерно (seed), от которого зависит вся последовательность.

Важно понимать ограничения: простая реализация может давать предсказуемые результаты и не подходит для криптографических задач. Однако она отлично демонстрирует внутреннюю механику генераторов и позволяет экспериментировать с настройками.

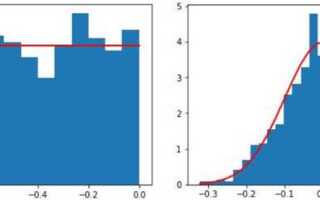
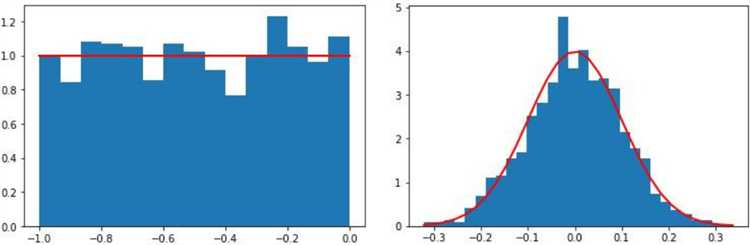
Для повышения качества генерации можно добавить нормализацию к диапазону [0, 1] и использовать комбинацию нескольких генераторов. Также стоит протестировать результаты с помощью критериев равномерности, например, критерия хи-квадрат.

Создание генератора случайных чисел без встроенных библиотек

Для реализации генератора случайных чисел без использования стандартных библиотек Python потребуется собственная реализация детерминированного алгоритма. Один из самых доступных вариантов – линейный конгруэнтный метод (LCG).

Алгоритм задаётся формулой:

X_n+1 = (a * X_n + c) % m

X_n – текущее значение (начинается с seed)
a – множитель
c – приращение
m – модуль

Рекомендованные параметры (взяты из Numerical Recipes):

a = 1664525
c = 1013904223
m = 232

Пример реализации:

class SimpleLCG:
def __init__(self, seed):
self.a = 1664525
self.c = 1013904223
self.m = 232
self.state = seed
def next(self):
self.state = (self.a * self.state + self.c) % self.m
return self.state
def random(self):
return self.next() / self.m

Инициализируйте генератор, передав seed – начальное значение.
Вызовите метод next() для получения псевдослучайного целого числа.
Используйте random() для получения значения от 0 до 1.

Важно: качество генератора зависит от параметров и начального состояния. Один и тот же seed всегда даст одинаковую последовательность, что полезно для воспроизводимости, но неприемлемо для криптографических задач.

Как реализовать линейный конгруэнтный метод на Python

Линейный конгруэнтный генератор (LCG) задаётся формулой: X_n+1 = (aX_n + c) mod m, где a – множитель, c – приращение, m – модуль, X₀ – начальное значение (seed). Успешность метода зависит от правильного выбора параметров: m – как правило степень 2 (например, 2³²), a – кратное 4k+1, c – нечётное и взаимно простое с m.

Пример на Python:

class LCG:
def __init__(self, seed=1, a=1664525, c=1013904223, m=2**32):
self.a = a
self.c = c
self.m = m
self.state = seed
def next(self):
self.state = (self.a * self.state + self.c) % self.m
return self.state
def random(self):
return self.next() / self.m

Используемый набор параметров (a = 1664525, c = 1013904223, m = 2³²) соответствует реализации из библиотеки ANSI C. Метод next() возвращает следующее целое псевдослучайное число, random() – число с плавающей точкой в диапазоне [0, 1).

Для получения последовательности достаточно вызвать генератор несколько раз:

gen = LCG(seed=12345)
for _ in range(5):
print(gen.random())

Стоит избегать использования LCG в криптографических задачах: несмотря на высокую скорость, его предсказуемость делает метод непригодным для защиты данных.

Проверка равномерности распределения сгенерированных чисел

Для оценки качества генератора случайных чисел необходимо проверить, насколько равномерно распределены выходные значения. Один из надёжных способов – анализ частот появления чисел в заданном диапазоне. Предположим, генератор выдаёт целые значения от 0 до 9 включительно. Зафиксируем количество генераций, например, 10000, и посчитаем, сколько раз встречается каждое значение.

Реализация на Python:

from collections import Counter
def custom_rng(seed, count):
a, c, m = 17, 43, 100
numbers = []
for _ in range(count):
seed = (a * seed + c) % m
numbers.append(seed % 10)
return numbers
result = custom_rng(seed=7, count=10000)
freq = Counter(result)
for num in sorted(freq):
print(f"{num}: {freq[num]}")

В идеале каждый элемент от 0 до 9 должен появиться около 1000 раз. Расхождения до 5% допустимы. Существенные отклонения свидетельствуют о смещении генератора. Для более точной оценки можно использовать критерий χ²:

import scipy.stats as stats
expected = [1000] * 10
observed = [freq[i] for i in range(10)]
chi2, p = stats.chisquare(f_obs=observed, f_exp=expected)
print(f"Chi² = {chi2:.2f}, p-value = {p:.4f}")

Если p-value выше 0.05, распределение можно считать равномерным. Если ниже – генератор требует доработки. Результат зависит от параметров алгоритма и начального значения. Для повышения качества рекомендуется подбирать коэффициенты генератора так, чтобы длина периода была близка к модулю, а модуль – простым числом.

Добавление поддержки генерации вещественных чисел

Для расширения функциональности генератора случайных чисел необходимо реализовать поддержку вещественных значений с заданной точностью. Это потребует изменения логики генерации и учета диапазона с плавающей точкой.

Используйте модуль random только для сравнения и проверки точности. Основной алгоритм остаётся ручной.
Выберите нужный диапазон, например от min_val = 1.0 до max_val = 10.0, и точность, например precision = 3 знака после запятой.
Преобразуйте диапазон в целые числа, умножив границы на 10 ** precision. Пример: min_int = int(min_val * 1000), max_int = int(max_val * 1000).
Используйте свой генератор целых чисел для получения случайного значения в новом диапазоне: rand_int = custom_randint(min_int, max_int).
Преобразуйте результат обратно в вещественное число: rand_float = rand_int / 1000.

Для контроля точности используйте round(rand_float, precision). Это исключит артефакты округления, особенно при сравнении значений. Такой подход сохраняет контроль над генерацией и не требует сторонних библиотек.

Настройка генератора для воспроизводимости результатов (seed)

Для получения одинаковой последовательности случайных чисел при каждом запуске программы необходимо установить значение seed. В Python это делается с помощью функции random.seed() из модуля random. Например: random.seed(42) – гарантирует, что генератор будет выдавать одну и ту же последовательность при каждом запуске с этим значением.

Число, передаваемое в seed(), может быть любым хэшируемым объектом, но на практике используют целые числа. Важно не менять значение seed внутри одной сессии, если требуется стабильность результатов.

В модуле numpy используется отдельная система генерации случайных чисел. Чтобы получить воспроизводимость с использованием NumPy, нужно создать генератор с заданным seed: rng = numpy.random.default_rng(42). Это предпочтительнее старого подхода через numpy.random.seed(), поскольку обеспечивает изоляцию состояния генератора.

При работе с многопоточностью или параллельными вычислениями каждый поток должен получать свой генератор с собственным seed. Это исключает нежелательные пересечения и повышает предсказуемость модели.

Для сложных проектов рекомендуется сохранять значение seed в конфигурационном файле или как часть входных данных эксперимента. Это обеспечивает полное восстановление условий генерации при отладке или повторном запуске.

Ограничение диапазона генерируемых чисел вручную

Для ограничения диапазона генерируемых чисел в Python можно использовать несколько методов. Один из наиболее распространенных подходов – использование стандартной библиотеки random с модификацией входных параметров. Например, чтобы генерировать случайное число в диапазоне от минимального значения min_val до максимального max_val, можно воспользоваться функцией random.randint(min_val, max_val).

Для более точного контроля над диапазоном, можно создавать свою собственную функцию генератора случайных чисел. В таком случае важно учитывать корректную настройку границ. Например, если диапазон должен быть только положительным, можно добавить дополнительную проверку на знак числа.

Пример простого генератора с ограничением диапазона от 1 до 100:

import random
def custom_random(min_val, max_val):
if min_val >= max_val:
raise ValueError("Минимальное значение должно быть меньше максимального.")
return random.randint(min_val, max_val)
print(custom_random(1, 100))

При создании собственного генератора важно удостовериться, что диапазон правильно обрабатывает граничные условия, чтобы избежать ошибок, например, при введении идентичных значений для минимального и максимального диапазона. Для этого рекомендуется реализовывать обработку исключений.

Если необходимо сгенерировать несколько чисел в одном диапазоне, то лучше воспользоваться циклом с функцией генерации чисел. Важно помнить, что такие генераторы не всегда гарантируют равномерное распределение, особенно если диапазон значений велик. В этом случае стоит использовать более сложные методы генерации, например, с применением библиотеки numpy для работы с массивами чисел.

Тестирование производительности самодельного генератора

При разработке собственного генератора случайных чисел важно не только корректное функционирование алгоритма, но и его производительность. Тестирование производительности позволяет выявить узкие места, оптимизировать код и обеспечить необходимую скорость работы при больших объемах данных.

Для тестирования производительности следует использовать подходы, которые точно измеряют время работы генератора на различных объемах данных. Один из самых простых способов – это использование встроенного модуля time, который позволяет засечь время выполнения функции генерации чисел. Например, можно замерить время генерации 1 миллиона случайных чисел:

import time
start = time.time()
for _ in range(1000000):
random_number = my_random_function()
end = time.time()
print(f"Время выполнения: {end - start} секунд")

Также важно учесть влияние количества чисел на скорость работы. Если производительность падает с увеличением числа генераций, возможно, стоит подумать о более эффективных алгоритмах или оптимизации текущего кода.

Для более точных измерений производительности можно использовать модуль timeit, который предназначен для высокоточного замера времени работы Python-кода. Он автоматически выполняет код несколько раз и вычисляет среднее время. Это важно, так как при использовании time результаты могут варьироваться из-за внешних факторов, таких как загрузка процессора.

Пример использования timeit для тестирования генератора:

import timeit
execution_time = timeit.timeit('my_random_function()', globals=globals(), number=1000000)
print(f"Среднее время выполнения: {execution_time} секунд")

Кроме того, важно проверить стабильность работы генератора на больших объемах данных. Если он начинает выдавать одинаковые числа или сильно замедляется при увеличении количества генерируемых значений, следует обратить внимание на возможные проблемы с алгоритмом или его реализацией.

Для комплексных тестов можно замерить не только время, но и качество случайных чисел. Это можно сделать с помощью статистических тестов, таких как проверка равномерности распределения чисел. Например, проверив, что генерируемые числа распределяются на интервале правильно и случайным образом.

Вопрос-ответ:

Как работает генератор случайных чисел на Python?

Генератор случайных чисел на Python использует алгоритмы для создания чисел, которые кажутся случайными. В стандартной библиотеке Python для этого используется модуль `random`, который предоставляет функции для генерации чисел в различных диапазонах. Например, функция `random.randint(a, b)` генерирует случайное целое число между a и b, а `random.random()` возвращает число с плавающей запятой от 0 до 1.

Как можно улучшить качество случайных чисел, генерируемых в Python?

Если требуется более высокая степень случайности (например, для криптографических целей), то вместо модуля `random` стоит использовать `secrets`. Этот модуль использует более стойкие алгоритмы, которые сложнее предсказать. Важно отметить, что для большинства повседневных задач стандартного генератора чисел будет вполне достаточно.

Что такое псевдослучайные числа и чем они отличаются от настоящих случайных чисел?

Псевдослучайные числа — это числа, которые генерируются с использованием алгоритмов, но их последовательность выглядит случайной. Однако, они на самом деле детерминированы начальным значением (seed). В отличие от настоящих случайных чисел, которые получаются, например, с помощью физического процесса, псевдослучайные числа можно повторно генерировать при тех же начальных условиях. Для большинства задач этого вполне достаточно, но для криптографических целей нужны более сложные источники случайности.

Можно ли использовать генератор случайных чисел для тестирования программного обеспечения?

Да, генератор случайных чисел часто используется для тестирования программного обеспечения, например, при тестировании на случайных входных данных или для проведения стресс-тестов. Это позволяет обнаружить возможные ошибки, которые могут проявиться при работе с нештатными входами. Однако важно обеспечить, чтобы тестовые данные были разнообразными и не имели предсказуемых паттернов, что может снизить качество тестирования.