Как написать корень числа в python

Вычисление корня числа в Python – одна из базовых операций, доступных в языке программирования. Существует несколько методов для вычисления квадратного корня, каждый из которых имеет свои особенности и преимущества в зависимости от задачи. Главная цель этой статьи – рассмотреть способы вычисления корня и предложить оптимальные решения для различных случаев.

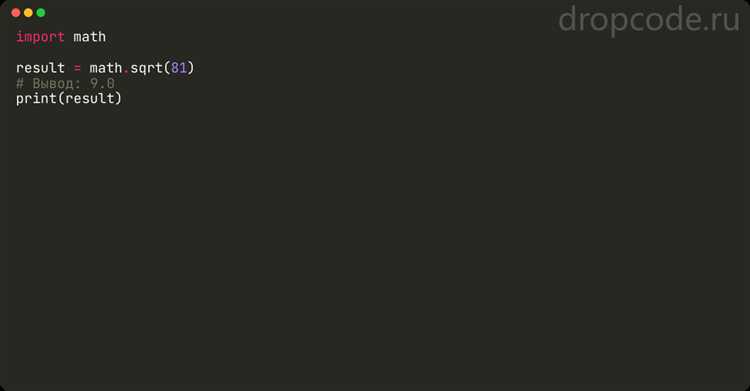
Первый и самый очевидный способ – использование встроенной функции sqrt() из модуля math. Эта функция возвращает квадратный корень числа, но только если входное значение является положительным числом. Например, math.sqrt(9) вернет 3.0. Важно помнить, что попытка вычислить корень из отрицательного числа вызовет ошибку.

Однако иногда необходимо работать с корнями других степеней. В таких случаях стоит использовать операцию возведения в степень, например, число (1/показатель степени). Для вычисления, например, кубического корня, можно использовать запись число (1/3). Этот способ более универсален, так как позволяет работать с любыми степенями.

Дополнительным вариантом является использование библиотеки numpy, которая предоставляет функции для работы с массивами данных и может быть полезна при выполнении вычислений для множества значений одновременно. Например, numpy.sqrt() действует аналогично функции из модуля math, но может работать с массивами, что существенно ускоряет обработку больших данных.

Использование оператора возведения в степень для вычисления корня

В Python для вычисления корня числа можно использовать оператор возведения в степень ``. Этот оператор позволяет выразить извлечение корня как возведение числа в дробную степень. Например, чтобы вычислить квадратный корень из числа, достаточно возвести его в степень 0.5.

число = 25
корень = число  0.5
print(корень)  # Выведет 5.0

Этот подход применим и для вычисления корня другой степени. Для извлечения корня любой степени, нужно возвести число в дробную степень, которая является обратной данной степени. Например, для вычисления кубического корня из числа нужно возвести его в степень 1/3.

Пример вычисления кубического корня:

число = 27
корень_куба = число  (1/3)
print(корень_куба)  # Выведет 3.0

При использовании оператора `` важно учитывать, что для отрицательных чисел результат может не совпадать с ожидаемым, если степень дробная. Это связано с особенностями работы с комплексными числами в Python, так как извлечение нецелых корней из отрицательных чисел может привести к ошибке. В таких случаях стоит использовать дополнительные проверки или подходы, чтобы избежать некорректных вычислений.

Использование оператора возведения в степень для вычисления корней особенно удобно в математических задачах, где требуется быстрое извлечение корней различной степени без необходимости импорта дополнительных библиотек.

Применение функции math.sqrt() для нахождения квадратного корня

Для использования этой функции необходимо импортировать модуль import math. В качестве аргумента функция принимает одно число и возвращает его квадратный корень. Например, вызов math.sqrt(16) вернёт значение 4.0.

Важно отметить, что math.sqrt() работает только с неотрицательными числами. Попытка передать отрицательное число вызовет ошибку ValueError, так как функция не поддерживает работу с комплексными числами. Для работы с отрицательными числами можно использовать модуль cmath, который поддерживает вычисления с комплексными числами.

При вычислениях с math.sqrt() всегда возвращается число с плавающей точкой. Например, даже если вы передадите целое число, результат будет в формате float. Это поведение следует учитывать при дальнейшем использовании полученных значений.

Пример корректного использования функции:

import math
result = math.sqrt(25)
print(result)  # Выведет: 5.0

Если необходимо выполнить проверку на отрицательное число до применения функции, можно использовать условие:

import math
number = -9
if number >= 0:
result = math.sqrt(number)
print(result)
else:
print("Ошибка: число не может быть отрицательным")

Для повышения производительности при работе с большими объемами данных можно заранее проверять, что входные данные не содержат отрицательных значений, что избавит от лишних проверок во время вычислений.

Вычисление корня произвольной степени с помощью оператора ``

В Python для извлечения корня произвольной степени используют оператор возведения в степень ``. Чтобы найти корень n-й степени из числа x, выражение записывается как x (1/n).

• Корень квадратный: 25 (1/2) → 5.0
• Корень кубический: 27 (1/3) → 3.0
• Корень четвёртой степени: 81 (1/4) → 3.0

Для корректного результата:

1. Убедитесь, что число положительное при извлечении чётного корня. Например, (-16) (1/2) вызовет ValueError при использовании с типом float.
2. Для работы с отрицательными числами при нечётной степени используйте вещественные степени: (-8) (1/3) → nan, но math.copysign(abs(-8) (1/3), -1) → -2.0.
3. Избегайте целочисленного деления: 1/3, а не 1//3, иначе результат будет некорректным.

def root(x, n):
if x < 0 and n % 2 == 0:
raise ValueError("Чётный корень из отрицательного числа невозможен.")
return x  (1 / n)

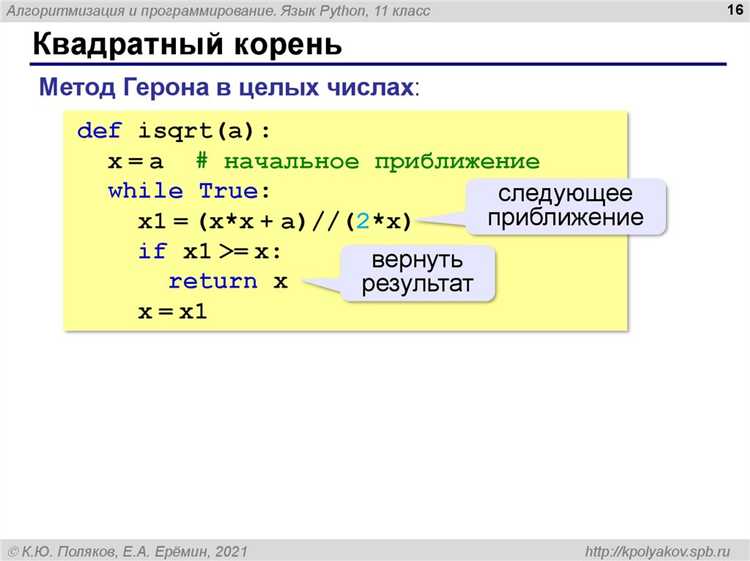
Реализация вычисления корня через алгоритм Ньютона

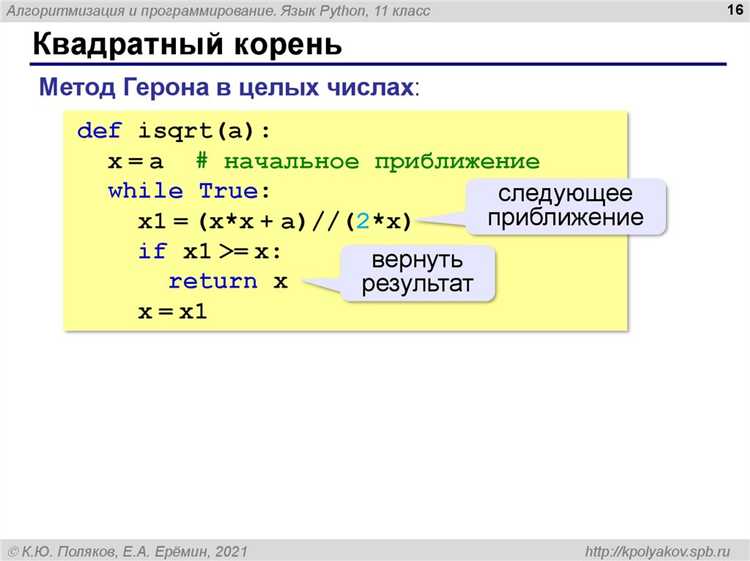
Алгоритм Ньютона (метод Ньютона-Рафсона) применим для приближённого вычисления квадратного корня из числа n с использованием итерационного процесса. Формула обновления: x = (x + n / x) / 2.

Реализация:

def sqrt_newton(n, tolerance=1e-10, max_iterations=1000):
if n < 0:
raise ValueError("Число должно быть неотрицательным")
if n == 0:
return 0
x = n
for _ in range(max_iterations):
next_x = 0.5 * (x + n / x)
if abs(x - next_x) < tolerance:
return next_x
x = next_x
raise RuntimeError("Превышено число итераций")

При вызове sqrt_newton(25) функция вернёт значение, близкое к 5. При передаче отрицательного аргумента вызывается исключение. Параметр tolerance задаёт точность, а max_iterations – защиту от зацикливания.

Метод Ньютона демонстрирует квадратичную скорость сходимости. Для корректной работы начальное приближение выбирается равным n, что обеспечивает устойчивость алгоритма при положительных n.

Работа с комплексными числами при вычислении корня

Для извлечения корня из комплексного числа в Python используется модуль cmath, так как встроенный math.sqrt() не поддерживает комплексные аргументы и вызывает ValueError при попытке вычислить корень из отрицательного числа.

Функция cmath.sqrt() возвращает корень в виде комплексного числа даже при положительном действительном аргументе. Пример:

import cmath
z = -4
root = cmath.sqrt(z)
print(root)  # (0+2j)

Чтобы извлечь корень из произвольного комплексного числа, например z = 3 + 4j, достаточно передать его напрямую:

z = 3 + 4j
root = cmath.sqrt(z)
print(root)  # (2+1j)

Результат извлечения корня из комплексного числа неоднозначен. Всегда существует два корня. cmath.sqrt() возвращает один из них – тот, у которого ненулевая часть находится в верхней полуплоскости (или на положительной оси при действительном результате).

Если требуется оба корня, второй можно получить, взяв отрицание первого:

z = 1 + 1j
root1 = cmath.sqrt(z)
root2 = -root1

Для вычисления корня n-й степени от комплексного числа используйте формулу через полярное представление:

def complex_nth_root(z, n):
r, phi = cmath.polar(z)
roots = [cmath.rect(r**(1/n), (phi + 2 * cmath.pi * k) / n) for k in range(n)]
return roots
roots = complex_nth_root(1 + 1j, 3)

Каждое значение в roots – один из n корней исходного комплексного числа. Это важно при решении уравнений и при работе с сигналами в спектральной области.

Как избежать ошибок при вычислении корня отрицательных чисел

В Python попытка вычислить квадратный корень отрицательного числа с помощью функции math.sqrt() вызывает ошибку ValueError, так как модуль math работает только с действительными числами. Например:

import math
math.sqrt(-9) # ValueError: math domain error

Чтобы избежать ошибки, необходимо использовать модуль cmath, предназначенный для работы с комплексными числами. Он корректно обрабатывает корни отрицательных чисел, возвращая комплексное значение:

import cmath
result = cmath.sqrt(-9)
print(result) # (0+3j)

Если нужно работать исключительно с действительными числами, следует заранее проверять знак подкоренного выражения и, при необходимости, обрабатывать его отдельно:

import math
def safe_sqrt(x):
    if x < 0:
        raise ValueError("Невозможно извлечь корень из отрицательного числа")
    return math.sqrt(x)

Также важно учитывать, что 0.5 и pow() при отрицательном основании и дробной степени ведут себя аналогично math.sqrt() и тоже вызывают ValueError:

(-9) 0.5 # ValueError в интерактивной среде
pow(-9, 0.5) # ValueError

Для корректной обработки таких выражений нужно использовать cmath.pow() или complex:

import cmath
result = (-9+0j) 0.5
print(result) # (0+3j)

import numpy as np
arr = np.array([4, 9, 16, 25], dtype=float)
roots = np.sqrt(arr)
print(roots)  # [2. 3. 4. 5.]

arr = np.array([4, -9, 16, -25], dtype=float)
roots = np.sqrt(np.where(arr >= 0, arr, np.nan))
print(roots)  # [ 2. nan  4. nan]

arr = np.array([8, 27, 64], dtype=float)
cube_roots = arr  (1/3)
print(cube_roots)  # [2. 3. 4.]

Если требуется сохранить исходный тип данных и избежать nan, можно применить np.abs() перед извлечением корня, но это исказит знак результата.

Тестирование точности вычислений при большом количестве корней

При вычислении корней большого количества чисел важно учитывать накопление ошибок округления, особенно при использовании чисел с плавающей запятой. Для анализа точности стоит протестировать разные подходы на больших выборках и сравнить результаты с эталонными значениями.

• Сгенерируйте массив из 1 000 000 положительных чисел в диапазоне от 1 до 10⁶, например, с помощью numpy.random.uniform(1, 1e6, size=106).
• Рассчитайте квадратные корни с использованием numpy.sqrt, math.sqrt и возведения в степень 0.5.
• Сравните полученные результаты с помощью numpy.allclose при rtol=1e-12 и atol=0 для выявления расхождений.
• Для оценки максимального отклонения используйте numpy.max(numpy.abs(результат - эталон)).
• Фиксируйте тип данных. Для высокой точности используйте numpy.float64. Проверка на float32 покажет значительное снижение точности, особенно при больших значениях входных данных.

Рекомендуется дополнительно протестировать стабильность при последовательных операциях, например, повторное возведение результата в квадрат. Значения, отличающиеся от исходных более чем на 1e-10, должны считаться неточными.

При работе с большим количеством вычислений предпочтительно использовать numpy.sqrt, так как он быстрее и устойчивее к накоплению ошибок векторных операций. Функция math.sqrt подходит только для скалярных вычислений и не обеспечивает преимущества при обработке массивов.

Вопрос-ответ: