Как найти наибольший общий делитель python

Наибольший общий делитель (НОД) двух или более чисел – это наибольшее число, которое делит все данные числа без остатка. В Python есть несколько способов вычисления НОД, включая использование встроенных функций и алгоритмов, таких как алгоритм Евклида, который обеспечивает быструю и эффективную реализацию. Знание этого алгоритма может быть полезным в различных задачах, связанных с числовыми операциями, теорией чисел и оптимизацией вычислений.

Для поиска НОД в Python можно использовать стандартную библиотеку math, которая включает функцию gcd (greatest common divisor). Это решение является простым и надежным, однако для более глубокого понимания и оптимизации кода полезно будет освоить алгоритм Евклида. Важно понимать, как работает эта математическая техника, поскольку она лежит в основе многих криптографических методов и алгоритмов сжатия данных.

Алгоритм Евклида основан на принципе: если два числа a и b делятся на какое-то число, то и числа b и a % b делятся на это же число. Алгоритм работает итеративно, сокращая одно из чисел в каждом шаге, пока одно из чисел не станет равным нулю. Это делает процесс нахождения НОД быстрым и эффективным, даже для больших чисел.

Как использовать алгоритм Евклида для нахождения НОД

Для двух чисел a и b алгоритм Евклида работает следующим образом:

1. Если b = 0, то НОД(a, b) = a.

2. Иначе, вычисляем остаток от деления a на b, обозначаем его r = a % b.

3. Повторяем процесс для чисел b и r, то есть теперь ищем НОД(b, r).

Этот процесс продолжается до тех пор, пока остаток от деления не станет равным нулю. Когда это случится, оставшееся ненулевое число и будет наибольшим общим делителем.

Пример на Python:

def euclid_gcd(a, b):
while b != 0:
a, b = b, a % b
return a

В данном примере переменные a и b обмениваются значениями: на каждом шаге b заменяется на остаток от деления a на b. Когда b становится равным нулю, оставшееся значение a и будет НОД.

Алгоритм Евклида работает эффективно, даже для очень больших чисел, так как на каждом шаге величина одного из чисел значительно уменьшается. Время работы алгоритма пропорционально логарифму от меньшего из двух чисел, что делает его одним из наиболее быстрых методов нахождения НОД.

Этот алгоритм применим не только для целых чисел, но и для чисел с плавающей точкой, если их привести к целым числам с помощью умножения на подходящую степень 10. Также алгоритм можно использовать для вычислений в различных областях математики и криптографии, где важна высокая скорость вычислений НОД.

Как найти НОД для нескольких чисел с помощью Python

Пример кода для нахождения НОД для нескольких чисел:

import math
from functools import reduce
def find_gcd_of_list(numbers):
return reduce(math.gcd, numbers)
numbers = [24, 36, 48]
result = find_gcd_of_list(numbers)
В этом примере список [24, 36, 48] передается в функцию find_gcd_of_list, которая последовательно находит НОД всех чисел. Функция reduce() применяет функцию math.gcd() к каждому числу списка, пока не останется один результат – НОД для всего списка.
Если необходимо работать с большим количеством чисел, это решение будет эффективно, так как reduce() выполняет операцию поочередно, что исключает необходимость вручную рассчитывать НОД для каждого элемента.
Также важно помнить, что в случае списка из одного числа НОД будет равен этому числу, так как любое число делится на себя.
Как применить встроенную функцию math.gcd для вычисления НОД

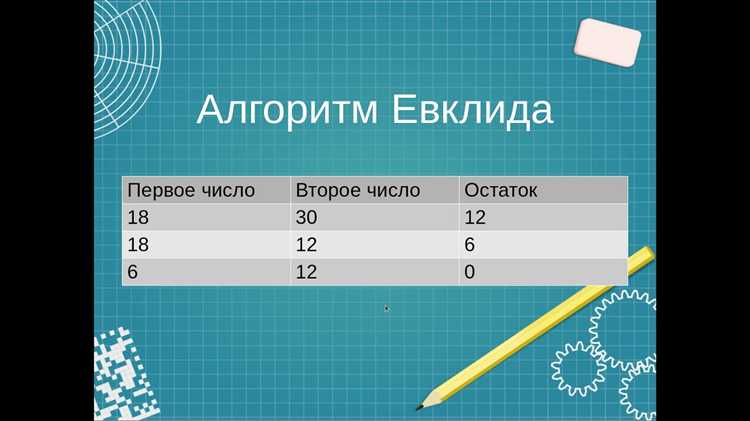
В Python для нахождения наибольшего общего делителя (НОД) двух чисел удобно использовать встроенную функцию math.gcd() из модуля math. Эта функция реализует эффективный алгоритм Евклида, что позволяет быстро и точно находить НОД.
Функция math.gcd(a, b) принимает два аргумента a и b – целые числа, для которых нужно вычислить НОД. Результат работы функции – наибольший общий делитель этих чисел.
Пример использования функции:
import math
a = 36
b = 60
nod = math.gcd(a, b)
print(nod)
Этот код выведет 12, так как наибольший общий делитель чисел 36 и 60 – это 12.
Важно отметить, что функция возвращает только целое число, равное НОД. Если одно из чисел равно 0, функция возвращает значение другого числа, так как НОД для числа и 0 равен самому числу. Например:
import math
a = 0
b = 5
nod = math.gcd(a, b)
print(nod)
Этот код выведет 5, поскольку НОД для 0 и 5 – это 5.
Основные рекомендации при использовании math.gcd():

Для работы с отрицательными числами результат будет таким же, как для положительных чисел. Например, math.gcd(-36, 60) вернёт тот же результат, что и для math.gcd(36, 60).
Если оба числа равны 0, функция вернёт 0. Однако это не является стандартным математическим случаем, и в реальных задачах лучше заранее проверять такие ситуации.
Для более сложных вычислений с несколькими числами можно использовать reduce из модуля functools, чтобы последовательно вычислять НОД для всех чисел в списке.

Пример для нескольких чисел:
from functools import reduce
import math
numbers = [36, 60, 48]
nod = reduce(math.gcd, numbers)
print(nod)
Этот код находит НОД для всех чисел в списке, в данном случае результат будет 12.
Как найти НОД для чисел с плавающей точкой в Python

Для нахождения наибольшего общего делителя (НОД) для чисел с плавающей точкой в Python необходимо сначала преобразовать числа в целые, так как стандартный алгоритм Евклида работает только с целыми числами. Этот процесс можно выполнить с помощью умножения чисел на соответствующие степени десяти, чтобы избавиться от дробной части.
Для начала преобразуем оба числа в целые. Например, для чисел с плавающей точкой 3.75 и 2.5, можно умножить их на 100, чтобы избавиться от десятичных знаков. Это даст 375 и 250, которые являются целыми числами. После этого можно найти НОД этих целых чисел с помощью алгоритма Евклида.
Пример кода для нахождения НОД чисел с плавающей точкой:

import math
def find_gcd_float(a, b):
# Преобразуем числа в целые
factor = 10 ** max(len(str(a).split('.')[1]), len(str(b).split('.')[1])))
a_int = int(a * factor)
b_int = int(b * factor)
# Находим НОД для целых чисел
return math.gcd(a_int, b_int)
# Пример использования
a = 3.75
b = 2.5
print(find_gcd_float(a, b))  # Выведет НОД

Этот метод позволяет найти НОД для чисел с плавающей точкой без значительных потерь точности, так как мы оперируем целыми числами, а не вещественными числами.
Важно учитывать, что при работе с числами с плавающей точкой могут возникать проблемы точности из-за особенностей представления вещественных чисел в компьютерах. Для более точных вычислений можно использовать типы данных, которые обеспечивают большую точность, такие как Decimal из библиотеки decimal.
В случае работы с большими числами с плавающей точкой или высокими требованиями к точности, использование метода с типом Decimal может быть более предпочтительным, так как он минимизирует погрешности округления.
Как оптимизировать код для нахождения НОД в больших числах

При работе с большими числами для нахождения наибольшего общего делителя (НОД) важно использовать алгоритмы, которые минимизируют количество операций и эффективно справляются с большими входными данными. Для этого можно применять несколько подходов, начиная от алгоритма Евклида и заканчивая его улучшенными версиями.
Первый шаг в оптимизации – это выбор правильного алгоритма. Классический алгоритм Евклида, хотя и эффективен, можно улучшить с помощью метода "бинарного Евклида", который использует операции деления пополам, что особенно эффективно при работе с большими числами.
Вот пример реализации оптимизированного алгоритма Евклида с использованием двоичных операций для нахождения НОД двух чисел:
def binary_gcd(a, b):
if a == b:
return a
if a == 0:
return b
if b == 0:
return a
if ~a & 1:  # Проверяем четность a
if b & 1:
return binary_gcd(a >> 1, b)
else:
return binary_gcd(a >> 1, b >> 1) << 1
if ~b & 1:  # Проверяем четность b
return binary_gcd(a, b >> 1)
if a > b:
return binary_gcd((a - b) >> 1, b)
return binary_gcd((b - a) >> 1, a)

Этот метод уменьшает количество делений, заменяя их операциями сдвига, что значительно повышает производительность, особенно при работе с большими числами.
Для еще большего повышения скорости можно использовать такие библиотеки, как numpy или math, которые реализуют алгоритм Евклида на уровне оптимизированных C-библиотек. Встроенная функция math.gcd в Python использует алгоритм Евклида, который также реализован с использованием эффективных подходов для больших чисел.
Пример использования встроенной функции для нахождения НОД:
import math
a = 12345678901234567890
b = 98765432109876543210
gcd = math.gcd(a, b)

Кроме того, для работы с очень большими числами важно избегать излишнего преобразования типов. Преобразования между типами, например, из целых чисел в строки, могут замедлить работу программы при больших входных данных. Если числа очень большие, лучше использовать тип int, который в Python автоматически обрабатывает произвольную длину чисел.
Для многократных вычислений НОД в контексте больших массивов данных можно использовать параллельные вычисления, что также позволяет значительно ускорить процесс. Множество библиотек, таких как concurrent.futures, предоставляют удобные средства для параллельной обработки задач в Python.
Таким образом, для оптимизации нахождения НОД на больших числах ключевыми моментами являются выбор правильного алгоритма, использование оптимизированных библиотек и минимизация избыточных операций с данными. Это позволяет достичь значительного ускорения работы с большими числами при нахождении их НОД.
Как реализовать вычисление НОД с помощью рекурсии в Python

Алгоритм Евклида – минималистичное решение задачи нахождения наибольшего общего делителя двух чисел. Рекурсивная реализация основывается на том, что gcd(a, b) = gcd(b, a % b), пока b ≠ 0. Когда b = 0, результатом становится a.
def gcd(a, b):
if b == 0:
return a
return gcd(b, a % b)

Для проверки корректности используйте простые вызовы:

gcd(48, 18) вернёт 6
gcd(270, 192) вернёт 6
gcd(17, 13) вернёт 1

Функция работает только с неотрицательными целыми числами. При необходимости обработки отрицательных значений следует явно приводить аргументы к модулю:
def gcd(a, b):
a, b = abs(a), abs(b)
if b == 0:
return a
return gcd(b, a % b)

Если требуется гарантировать, что результат всегда неотрицателен – модуль следует применять только к результату, а не к аргументам, чтобы сохранить направление деления в случаях, где оно имеет значение (например, в криптографии).
Для чисел большого размера рекурсивный подход может привести к переполнению стека. В таких случаях используйте итеративную версию или включайте sys.setrecursionlimit() с осторожностью.
Вопрос-ответ: