Как найти выбросы в данных python

Выбросы в данных – это аномальные значения, значительно отличающиеся от других наблюдений. Эти значения могут существенно исказить результаты анализа, поэтому их важно выявлять и корректировать. Для обнаружения выбросов в Python существует несколько эффективных методов, основанных на статистических и машинных подходах. В этом материале мы рассмотрим основные способы работы с выбросами, применяя популярные библиотеки, такие как pandas, numpy, scipy и sklearn.

Простой, но эффективный способ – использование межквартильного диапазона (IQR). Этот метод помогает определить выбросы как значения, находящиеся за пределами 1.5 раз IQR от первого и третьего квартилей. Такой подход хорош тем, что не требует предположений о распределении данных, что делает его универсальным инструментом для различных типов данных. Важно помнить, что выбор коэффициента 1.5 является стандартным, но его можно настроить в зависимости от специфики задачи.

Другим распространенным методом является использование Z-оценки, которая измеряет отклонение наблюдения от среднего значения в терминах стандартных отклонений. Значения с Z-оценкой выше 3 или ниже -3 могут быть классифицированы как выбросы. Этот метод особенно полезен, когда данные имеют нормальное распределение, однако его эффективность может снизиться при наличии сильно скошенных данных.

Кроме того, для более сложных наборов данных, таких как многомерные, можно использовать методы машинного обучения, такие как кластеризация (например, алгоритм DBSCAN) или методы на основе деревьев решений. Эти методы позволяют не только обнаружить выбросы, но и понять, как они влияют на структуру данных. Важно тестировать несколько методов, чтобы выбрать наиболее подходящий для конкретной задачи.

Подготовка данных для анализа выбросов в Python

Для эффективного анализа выбросов важно подготовить данные, минимизируя влияние шума и ошибок. Основные этапы подготовки включают очистку данных, обработку пропусков, приведение переменных к нужному формату и стандартизацию. Каждый из этих шагов напрямую влияет на точность обнаружения выбросов.

Первый шаг – очистка данных. Выбросы могут быть следствием ошибок ввода, например, если возраст человека указан как 150 лет. Чтобы предотвратить это, необходимо использовать условия фильтрации. Например, с помощью библиотеки pandas можно удалить строки с аномальными значениями, например, те, у которых возраст больше 100 или меньше 0:

df = df[(df['age'] >= 0) & (df['age'] <= 100)]

Далее, обработка пропусков. Пропущенные значения могут искажать результаты, поэтому важно решать эту проблему до начала анализа. В зависимости от характера данных, пропуски можно заполнять средним, медианой или модой для числовых данных или наиболее частым значением для категориальных. Если пропусков слишком много, возможно, стоит удалить строки или столбцы. В pandas это можно сделать так:

df = df.dropna()

Для анализа выбросов часто используется стандартизация данных. Этот этап важен, когда переменные имеют разные масштабы, например, доход и возраст. Стандартизация приводит все данные к одному масштабу, что помогает в точной идентификации выбросов. Стандартное отклонение и среднее могут быть использованы для нормализации данных, как показано ниже:

from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
df_scaled = scaler.fit_transform(df[['feature1', 'feature2']])

Если данные имеют категориальные признаки, они должны быть преобразованы в числовые. Для этого используют кодирование категориальных переменных, например, с помощью one-hot encoding:

df = pd.get_dummies(df, columns=['category_column'])

Особое внимание стоит уделить анализу корреляций между переменными. Сильная корреляция между некоторыми признаками может привести к созданию ложных выбросов. В таком случае, может понадобиться исключить одну из высококоррелированных переменных. Это можно сделать с помощью метода корреляции:

correlation_matrix = df.corr()

Каждый из этих шагов значительно улучшает качество данных для анализа выбросов. Подготовка данных должна быть тщательной и систематичной, чтобы обеспечить корректный и надежный результат при поиске аномальных значений.

Использование метода IQR для выявления выбросов в числовых данных

Основная идея заключается в том, чтобы вычислить два квартиля: первый квартиль (Q1) и третий квартиль (Q3), а затем использовать их для нахождения межквартильного размаха (IQR), который равен разнице между Q3 и Q1:

IQR = Q3 - Q1

После вычисления IQR, выбросы можно определить как значения, находящиеся за пределами диапазона, который определяется следующим образом:

Нижняя граница = Q1 - 1.5 * IQR
Верхняя граница = Q3 + 1.5 * IQR

Данные, которые лежат ниже нижней границы или выше верхней границы, считаются выбросами. Этот метод хорошо работает для симметричных распределений, но может быть неэффективен для сильно асимметричных данных.

Пример использования метода IQR в Python с библиотекой pandas:

import pandas as pd
# Пример данных
data = pd.Series([10, 12, 14, 15, 100, 120, 130, 15, 16, 18])
# Вычисление квартилей
Q1 = data.quantile(0.25)
Q3 = data.quantile(0.75)
# Вычисление IQR
IQR = Q3 - Q1
# Определение границ для выбросов
lower_bound = Q1 - 1.5 * IQR
upper_bound = Q3 + 1.5 * IQR
# Фильтрация выбросов
outliers = data[(data < lower_bound) | (data > upper_bound)]
print(outliers)

В результате выполнения этого кода вы получите список значений, которые являются выбросами. Такой подход позволяет автоматически обнаруживать аномалии в числовых данных.

Метод IQR имеет несколько ограничений. Например, он может не распознать выбросы, если данные имеют много кластеров или если выбросы находятся близко к основным данным. Однако это простой и быстрый способ для предварительного анализа данных.

Обнаружение выбросов с помощью z-оценки в Python

Применение z-оценки для обнаружения выбросов в Python включает несколько ключевых шагов. Рассмотрим, как это сделать на примере библиотеки scipy и numpy.

Вычисление z-оценки. Для начала необходимо вычислить среднее значение и стандартное отклонение для каждого столбца данных. Z-оценка рассчитывается по формуле:

z = (x - mean) / std

где x – наблюдаемое значение, mean – среднее значение, std – стандартное отклонение.

Установка порога для выбросов. Обычно выбросами считаются те значения, чьи z-оценки больше 3 или меньше -3. Это означает, что такие значения находятся за пределами трех стандартных отклонений от среднего.

Для этого достаточно использовать библиотеку numpy, чтобы вычислить среднее и стандартное отклонение, а затем рассчитать z-оценки для всех наблюдений.

import numpy as np
# Пример данных
data = np.array([10, 12, 13, 15, 100, 14, 13, 12, 11, 10])
# Вычисление среднего и стандартного отклонения
mean = np.mean(data)
std = np.std(data)
# Расчет z-оценок
z_scores = (data - mean) / std
# Поиск выбросов
outliers = data[np.abs(z_scores) > 3]
print(outliers)

Этот код найдет все значения, для которых z-оценка превышает порог 3. В нашем примере значение 100 будет классифицировано как выброс.

Обработка выбросов. После обнаружения выбросов можно применить различные методы для их устранения или корректировки. Например:

Удаление выбросов из набора данных, если их влияние значительное;
Замена выбросов на среднее значение или медиану;
Использование методов машинного обучения, которые устойчивы к выбросам.

Метод z-оценки хорошо работает в случае нормального распределения данных, однако для распределений с сильными асимметриями или с тяжелыми хвостами могут потребоваться другие методы для обнаружения выбросов, такие как IQR (межквартильный размах) или методы кластеризации.

Таким образом, использование z-оценки – это эффективный и простой способ выявления выбросов в данных, особенно при нормальном распределении, с возможностью дальнейшей обработки для улучшения качества анализа.

Как применить алгоритмы машинного обучения для поиска аномалий

Для начала стоит отметить, что выбор алгоритма зависит от типа данных и задачи. Рассмотрим несколько популярных подходов:

1. Метод опорных векторов для обнаружения аномалий (One-Class SVM)

Этот метод используется для задач, где данные имеют одну доминирующую категорию, а аномалии должны быть выявлены относительно этой категории. One-Class SVM строит гиперплоскость, которая разделяет нормальные данные от аномальных. Алгоритм работает на основе концепции максимизации разделяющей границы, минимизируя ошибку классификации. Он эффективен в задачах, где аномалии редко встречаются и их трудно пометить заранее.

2. Лес из случайных деревьев (Isolation Forest)

Isolation Forest подходит для работы с большими наборами данных и высокоэффективен при обнаружении аномалий в данных с высокой размерностью. Алгоритм работает, создавая случайные разделяющие гиперплоскости (деревья), которые изолируют данные. Аномалии оказываются легче изолируемыми, поскольку они значительно реже встречаются в данных и требуют меньшего числа разделений для изоляции.

3. Кластеризация с использованием алгоритма DBSCAN

Алгоритм DBSCAN (Density-Based Spatial Clustering of Applications with Noise) использует плотность точек для разделения данных на кластеры. Точки, не принадлежащие ни одному кластеру, считаются аномалиями. Это эффективный метод для работы с данными, имеющими неравномерную плотность. DBSCAN хорошо работает в случаях, когда данные содержат шум или выбросы, которые можно игнорировать при кластеризации.

4. Алгоритм автокодировщиков (Autoencoders)

Автокодировщики – это нейронные сети, обучающиеся сжатию и восстановлению данных. Когда сеть обучена на нормальных данных, она будет плохо восстанавливать аномальные точки, так как они отличаются от обучающего набора. Чем хуже восстановление, тем вероятнее, что точка является аномалией. Этот метод хорошо подходит для данных с высокой размерностью, таких как изображения или временные ряды.

5. Метод k-ближайших соседей (k-NN)

Алгоритм k-NN используется для классификации, но может быть адаптирован для обнаружения аномалий. Он основан на предположении, что аномальные точки обычно не имеют много соседей в пространстве признаков. Для каждой точки рассчитывается среднее расстояние до её k ближайших соседей, и если оно значительно больше, чем у других точек, такая точка классифицируется как аномалия.

Рекомендации по выбору алгоритма:

При выборе алгоритма для поиска аномалий следует учитывать следующие факторы:

Тип данных: если данные непрерывные, алгоритмы, такие как One-Class SVM или Isolation Forest, могут дать хорошие результаты. Для категориальных данных подходит использование методов кластеризации.
Размер данных: для больших наборов данных рекомендуется использовать более эффективные методы, такие как Isolation Forest.
Наличие меток: если метки для аномальных точек отсутствуют, лучше применять безметочные методы, такие как DBSCAN или автоэнкодеры.

Каждый из этих методов имеет свои преимущества и ограничения. Важно протестировать несколько алгоритмов и выбрать наиболее подходящий для ваших данных и задачи. Настройка гиперпараметров, таких как количество ближайших соседей или плотность кластеров, также может существенно повлиять на результаты.

Визуализация выбросов с помощью графиков в Python

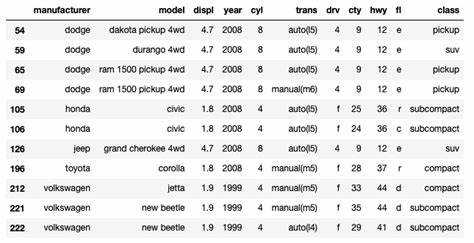
1. Гистограммы – один из самых простых способов визуализации распределения данных. Выбросы будут отображаться как значения, отдаленные от основной массы данных. При построении гистограммы важно выбрать правильное количество бинов (интервалов), чтобы не скрыть аномалии. Например, в библиотеке Matplotlib можно использовать функцию plt.hist(). Слишком большое количество бинов может создать иллюзию отсутствия выбросов, а слишком малое – привести к их маскировке.

2. Диаграммы размахов (Boxplot) – еще один удобный инструмент для поиска выбросов. Визуализируя распределение данных через медиану, квартили и возможные выбросы (точки, находящиеся за пределами 1.5 межквартильных расстояний от первого и третьего квартилей), можно легко выявить аномалии. В библиотеке Seaborn для построения диаграммы используется функция sns.boxplot(), которая позволяет сразу выделить выбросы и понять, как они влияют на данные.

3. Диаграммы рассеяния (Scatter plot) – подходят для анализа взаимосвязей между двумя переменными. Если на графике наблюдаются отдельные точки, которые значительно отклоняются от основной массы данных, это может быть признаком выбросов. В Matplotlib для этого используется функция plt.scatter(). Это особенно полезно, если нужно обнаружить выбросы, связанные с несколькими переменными.

4. Картограммы с плотностью (Density plot) – построение графиков плотности позволяет получить сглаженное представление о распределении данных. В отличие от гистограмм, они не зависят от выбора числа интервалов, что дает более объективную картину. В Seaborn можно построить такие графики с помощью sns.kdeplot().

5. Парные графики (Pairplot) – этот метод полезен, когда необходимо оценить выбросы в многомерных данных. Pairplot строит scatterplot для каждой пары признаков в наборе данных и включает диаграмму плотности для каждого признака. Это позволяет сразу увидеть взаимосвязи и возможные выбросы. Для построения такого графика в Seaborn используется функция sns.pairplot().

Для максимальной эффективности визуализации выбросов важно использовать правильные масштабы и компоновать графики таким образом, чтобы можно было легко сравнивать различные аспекты данных. При анализе выбросов всегда стоит учитывать контекст задачи, так как некоторые аномальные значения могут быть вполне допустимы или иметь важное значение.

Практическое применение и корректировка данных с выбросами

Для числовых данных часто используются методы на основе межквартильного расстояния (IQR). Это простой и эффективный способ выявления выбросов. Например, значения, находящиеся за пределами диапазона Q1 - 1.5 * IQR и Q3 + 1.5 * IQR, считаются выбросами. Такой подход работает в случаях, когда распределение данных примерно симметрично и не имеет явных сдвигов.

Когда данные сильно скошены или имеют сложное распределение, можно применять более продвинутые методы, такие как локальные методы, например, LOF (Local Outlier Factor). Эти методы учитывают плотность данных и могут быть полезны при анализе многомерных данных, где выбросы могут не проявляться явным образом в одномерных распределениях.

После того как выбросы были обнаружены, важно правильно выбрать метод их корректировки. В простых случаях можно заменить выбросы медианой или средним значением в пределах допустимого диапазона. Однако в задачах, где выбросы являются частью важной информации (например, в финансовых данных или при анализе аномальных событий), их удаление может привести к потере полезной информации. В таких случаях можно рассматривать использование моделей, устойчивых к выбросам, таких как регрессия с robust loss-функциями.

В случае с временными рядами, выбросы могут быть вызваны сезонными изменениями или аномальными событиями, которые необходимо учитывать при корректировке данных. Вместо удаления таких значений, можно применить технику сглаживания или интерполяции, которая позволит минимизировать их влияние на результат.

Некорректно обрабатывать выбросы может привести к снижению точности модели и ее неспособности обобщать на новые данные. Важно помнить, что нет универсального решения для корректировки выбросов. Каждый метод требует тестирования и верификации на основе особенностей конкретных данных.

Вопрос-ответ:

Как с помощью Python обнаружить выбросы в данных?

Для обнаружения выбросов в данных с помощью Python можно использовать различные методы. Один из них — это использование библиотеки pandas для работы с данными и matplotlib для визуализации. Популярным подходом является использование метода межквартильного размаха (IQR). Вычисляются 25-й и 75-й перцентили, затем определяется размах (между этими квартилями). Если значения данных выходят за пределы этого диапазона, их можно считать выбросами. Также часто используется метод z-оценки, при котором значения, отклоняющиеся от среднего более чем на 3 стандартных отклонения, считаются выбросами.

Что такое межквартильный размах (IQR) и как он помогает находить выбросы?

Межквартильный размах (IQR) — это разница между 75-м и 25-м процентилями (квартилями) распределения данных. Этот метод помогает определить, где сосредоточена основная масса данных и где начинается зона с выбросами. Если значение данных лежит за пределами диапазона от Q1−1.5×IQRQ1 - 1.5 \times IQRQ1−1.5×IQR до Q3+1.5×IQRQ3 + 1.5 \times IQRQ3+1.5×IQR, то оно считается выбросом. Такой подход часто применяется для числовых данных и помогает фильтровать аномалии, которые значительно отличаются от основного набора данных.

Можно ли обнаруживать выбросы с помощью машинного обучения в Python?

Да, с помощью машинного обучения в Python можно эффективно обнаруживать выбросы. Для этого можно использовать алгоритмы, такие как Isolation Forest, One-Class SVM или DBSCAN. Эти методы не требуют заранее заданного порога для определения выбросов и могут выявить аномальные точки даже в сложных многомерных данных. Например, Isolation Forest обучает модель, которая способна изолировать выбросы, и чем быстрее объект изолируется, тем более вероятно, что он является аномалией. Эти алгоритмы реализованы в библиотеке scikit-learn и могут быть полезны, если данные имеют сложную структуру.