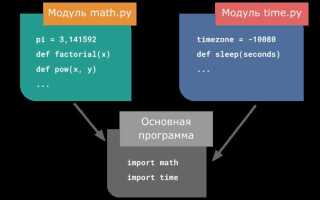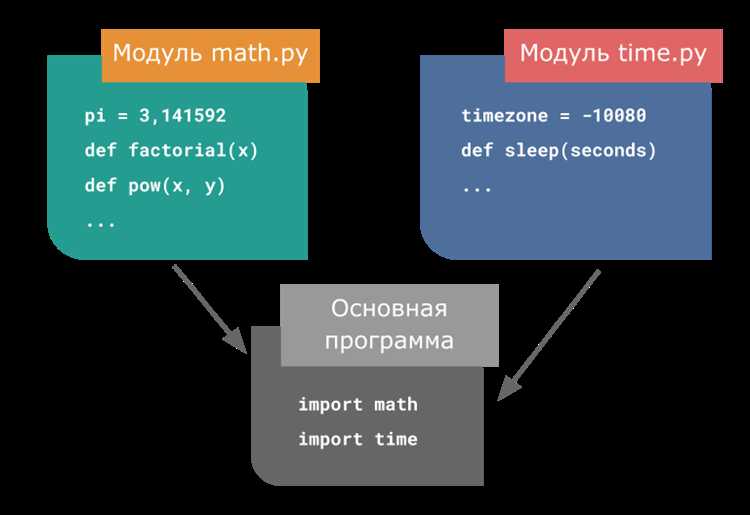
Библиотека math входит в стандартную поставку Python и предоставляет доступ к функциям и константам, которые реализованы на уровне C. Она применяется при выполнении вычислений, требующих повышенной точности и производительности, включая работу с тригонометрией, логарифмами, степенями и округлением.
Чтобы использовать функции модуля, необходимо выполнить команду import math. Это позволяет обращаться к методам через префикс math., например, math.sqrt(16) возвращает корень из 16. Для более лаконичного доступа допустим альтернативный синтаксис: from math import sqrt, но при этом не импортируются другие функции, если не указаны явно.
Константы math.pi и math.e используются при решении задач, связанных с кругами и экспонентами. В отличие от приближённых значений, эти константы определены с высокой точностью: math.pi ≈ 3.141592653589793, math.e ≈ 2.718281828459045.
Для округления доступны math.floor() и math.ceil(), возвращающие соответственно наибольшее целое, не превышающее число, и наименьшее целое, не меньшее числа. Это особенно полезно при математическом моделировании и оптимизации.
Тригонометрические функции, такие как math.sin(), math.cos() и math.tan(), принимают аргументы в радианах. При необходимости перевода градусов в радианы используется math.radians(), а обратное преобразование выполняется через math.degrees().
Функции math.log() и math.log10() предназначены для вычисления натурального и десятичного логарифмов. Если требуется логарифм по произвольному основанию, можно использовать форму math.log(x, base).
Модуль math не поддерживает работу с комплексными числами. Для таких задач следует использовать cmath, который реализует аналогичные функции, адаптированные для комплексной арифметики.
Как импортировать math и выбрать нужные функции
Для подключения библиотеки используйте команду import math. Она загружает весь модуль, после чего доступ к функциям осуществляется через префикс math., например: math.sqrt(9) возвращает 3.0.
Если требуется только часть функциональности, импортируйте конкретные объекты: from math import sin, pi. Это позволит использовать sin(pi / 2) без указания модуля.
Для экономии памяти и повышения читаемости избегайте полной загрузки модуля, если используется 1–2 функции. Например, при работе с тригонометрией чаще всего достаточно sin, cos и tan.
Не используйте конструкцию from math import *, поскольку она загружает всё содержимое в глобальное пространство имён, что может привести к конфликтам и снижает предсказуемость кода.
Чтобы узнать список доступных функций, выполните dir(math). Для получения справки по конкретной функции – help(math.log).
Чем отличается импорт всей библиотеки от выборочного импорта
При работе с модулем math в Python есть два способа подключения: полный импорт и выборочный. Каждый из них влияет на читаемость кода, производительность и потенциальные конфликты имён.
- Полный импорт:
import math - Выборочный импорт:
from math import sqrt, pi
Полный импорт требует обращения к функциям и константам через префикс math.. Это делает код более явным и снижает риск случайного переопределения имён:
import math
area = math.pi * math.pow(5, 2)При выборочном импорте функции и константы попадают напрямую в пространство имён, и можно использовать их без префикса:
from math import pi, pow
area = pi * pow(5, 2)- Полный импорт предпочтителен при использовании большого числа функций или если важно сохранить ясность происхождения каждой из них.
- Выборочный импорт уместен при использовании ограниченного набора объектов, особенно если имена не пересекаются с переменными в коде.
- Избегайте конструкции
from math import *, так как она затрудняет понимание, какие именно функции используются, и увеличивает риск конфликтов имён.
Если производительность критична, выборочный импорт может быть чуть быстрее при большом числе обращений к импортированным функциям, поскольку не используется доступ через объект модуля.
Как вычислить квадратный корень и степень с помощью math
Для извлечения квадратного корня используется функция math.sqrt(x), где x – число с плавающей точкой или целое число. Если передать отрицательное значение, возникнет ошибка ValueError.
Пример:
import math
результат = math.sqrt(25)
print(результат) # 5.0
Для возведения в степень применяется math.pow(a, b), где a – основание, b – показатель степени. Возвращается результат в виде числа с плавающей точкой независимо от типов аргументов.
Пример:
import math
степень = math.pow(2, 3)
print(степень) # 8.0
Функция math.pow отличается от оператора тем, что всегда возвращает float и обрабатывает только числовые значения. Оператор поддерживает и другие типы, включая complex.
Что нужно знать о работе с числами π и e
Число π доступно в модуле math как math.pi и имеет точность до 15 знаков после запятой: 3.141592653589793. Оно полезно при вычислении длины окружности, площади круга, углов в радианах и тригонометрических операций. Учитывайте, что точность math.pi достаточна для большинства инженерных задач, но при необходимости высокой точности используйте библиотеки с произвольной точностью, например, decimal.
Число e представлено как math.e и приближённо равно 2.718281828459045. Оно используется при вычислении экспоненты, логарифмов и в задачах, связанных с непрерывным ростом. Для возведения e в степень используйте math.exp(x) вместо math.e ** x, так как math.exp работает быстрее и точнее благодаря внутренней оптимизации.
Для получения логарифма по основанию e используйте math.log(x), а для других оснований – math.log(x, base). Не путайте math.log10(x) и math.log(x, 10): первый обычно быстрее, так как оптимизирован под логарифм по основанию 10.
Функции, работающие с π и e, не требуют ручного задания этих констант – их точные значения уже определены в модуле. Избегайте использования приближений вроде 3.14 или 2.71 – это снижает точность расчётов при повторных операциях.
Как округлять числа с помощью math.floor, math.ceil и math.trunc
Функция math.floor(x) возвращает наибольшее целое число, не превышающее x. Например, math.floor(3.9) даёт 3, а math.floor(-3.9) – -4. Это полезно, когда нужно получить нижнюю границу диапазона.
math.ceil(x) работает противоположным образом – возвращает наименьшее целое число, не меньшее x. Вызов math.ceil(3.1) даст 4, а math.ceil(-3.1) – -3. Такой подход подходит для верхних ограничений и расчётов, связанных с запасом.
math.trunc(x) отбрасывает дробную часть без округления. math.trunc(3.9) вернёт 3, math.trunc(-3.9) – -3. Это эквивалентно приведению к int, но через библиотеку math.
Во всех случаях аргумент должен быть числом с плавающей точкой. Для работы с массивами чисел рекомендуется использовать цикл или списковое включение. Пример: [math.floor(x) for x in [1.8, 2.3, 3.7]] вернёт [1, 2, 3].
Когда использовать тригонометрические функции из math
Тригонометрические функции из библиотеки math в Python необходимы при решении задач, связанных с углами и измерением величин, зависящих от них. Это особенно важно при обработке данных, полученных из сферических координат, графиков волн или векторных расчётов.
Если вам нужно работать с углами в радианах, а не в градусах, использование функций math.sin(), math.cos(), math.tan() будет предпочтительнее. Важным моментом является то, что стандартная библиотека Python требует радианы как входные параметры для тригонометрических функций. Для работы с углами в градусах их необходимо сначала преобразовать в радианы с помощью math.radians().
Когда требуется точная работа с углами, например, при моделировании движения объектов в физике или вычислениях на круге, эти функции предоставляют высокую точность и скорость работы. Они полезны для создания графиков колебаний, волн, при расчётах на основе Пифагора, а также для нахождения расстояний или углов между векторами в геометрии.
Применение функций math.atan2() важно в случаях, когда необходимо точно вычислить угол между двумя точками, учитывая их координаты на плоскости. Эта функция даёт более корректный результат, чем простое использование atan(), так как она принимает во внимание знак обеих координат, что важно для правильной интерпретации угла в различных квадрантах.
Тригонометрические функции удобно использовать в задачах, связанных с круговыми движениями или преобразованиями координат. Если задача включает вычисления с круговыми функциями или анализ колебаний, библиотеки math с её функциями типа math.sin(), math.cos(), math.tan() будут одними из самых быстрых и точных инструментов для решения этих проблем.
Как math работает с логарифмами и экспонентами
Библиотека math предоставляет два ключевых инструмента для работы с логарифмами и экспонентами: функции log и exp. Эти функции широко используются для математических вычислений, связанных с растущими и убывающими процессами, а также в аналитике и статистике.
Основные функции:
math.log(x, base)– вычисляет логарифм числаxпо основаниюbase. Если основание не указано, по умолчанию используется натуральный логарифм (основаниеe).math.exp(x)– вычисляет значение экспонентыe, возведённой в степеньx. Это функция для работы с экспоненциальным ростом.
Пример использования:
math.log(100)возвращает натуральный логарифм от 100.math.log(100, 10)вычисляет логарифм по основанию 10, что эквивалентноlog10(100).math.exp(1)даст значение числаe, равное приблизительно 2.71828.
Важно отметить, что функции log и exp активно используются в различных областях, включая решение дифференциальных уравнений, анализ роста и распада, статистику и прогнозирование.
Вопрос-ответ:
Что такое библиотека math в Python и как её подключить?
Библиотека math в Python предоставляет математические функции и константы, такие как математические операции, тригонометрические функции, логарифмы и т. д. Чтобы использовать её, нужно импортировать её в код с помощью команды import math.
Какие функции можно использовать в библиотеке math для работы с числами?
В библиотеке math есть множество полезных функций, например, math.sqrt() для вычисления квадратного корня, math.pow() для возведения в степень, math.sin() и math.cos() для тригонометрических вычислений. Есть также функции для работы с логарифмами, такими как math.log(), а также константы, такие как math.pi.
Как использовать функцию math.factorial()?
Функция math.factorial() вычисляет факториал числа. Например, math.factorial(5) вернёт результат 120, так как 5! = 5 × 4 × 3 × 2 × 1. Эта функция принимает только целые числа и возвращает факториал данного числа.
Можно ли использовать math для работы с комплексными числами?
Библиотека math не поддерживает операции с комплексными числами. Для работы с ними лучше использовать библиотеку cmath, которая специально предназначена для таких операций. Например, cmath.sqrt() может быть использована для извлечения квадратного корня из комплексного числа.
Что такое константа math.pi и как её использовать?
Константа math.pi в библиотеке math представляет число Пи, которое равно примерно 3.14159. Её часто используют в расчетах, связанных с кругами и углами. Например, для вычисления площади круга с радиусом 2 можно использовать выражение math.pi * 2 ** 2, что даст результат 12.56636.
Что такое библиотека math и как её подключить?
Библиотека math является стандартной в Python и предоставляет различные математические функции для выполнения вычислений, таких как работа с числами, вычисление тригонометрических функций и логарифмов. Чтобы использовать её, нужно просто импортировать с помощью команды: `import math`. После этого можно вызывать доступные функции библиотеки, например, `math.sqrt()` для извлечения квадратного корня или `math.sin()` для вычисления синуса угла.