Перевод чисел в двоичную систему – важная задача для программистов, особенно при работе с низкоуровневыми операциями, бинарными файлами или сетевыми протоколами. В Python существует несколько способов перевести десятичное число в двоичную форму. Знание этих методов поможет вам быстрее решать задачи, требующие манипуляций с числами в бинарном виде.
Стандартная библиотека Python предоставляет встроенную функцию bin(), которая преобразует число в строковое представление в двоичной системе. Например, bin(10) вернёт строку '0b1010'. Эта строка начинается с префикса '0b', который указывает на то, что число записано в двоичной системе счисления. В реальных приложениях вы можете столкнуться с необходимостью избавиться от этого префикса или, наоборот, использовать его.
Если вы хотите избежать использования встроенных функций, можно написать собственную функцию для перевода числа в двоичную систему. Этот подход поможет глубже понять, как происходит представление чисел в памяти и как работают бинарные операции. Простая реализация может использовать цикл, который делит число на 2 и записывает остатки от деления, формируя двоичную запись. Такой метод полезен для образовательных целей и углубленного изучения алгоритмов.
Использование встроенной функции bin() для перевода в двоичную систему
Функция bin() в Python позволяет легко и быстро перевести целое число в двоичное представление. Она принимает один аргумент – целое число, и возвращает строку, которая начинается с префикса '0b', указывающего на двоичную систему счисления.
Для примера, если мы хотим перевести число 10 в двоичную систему, можно использовать следующий код:
bin(10)Результатом выполнения будет строка '0b1010'. Часть '0b' служит индикатором того, что число записано в двоичной системе, а сама последовательность 1010 представляет число в двоичном формате.
Стоит учитывать, что bin() работает только с целыми числами, как положительными, так и отрицательными. Для отрицательных чисел функция возвращает строку с префиксом '-0b'. Например, при передаче -5 в функцию:
bin(-5)Результат будет '-0b101'.
Функция bin() всегда возвращает строку, даже если число равно 0. В этом случае результат будет '0b0'.
Также стоит помнить, что если задача требует получения только самих двоичных цифр без префикса '0b', можно воспользоваться срезом строки. Например:
bin(10)[2:]Этот код вернёт строку '1010', убрав префикс '0b'.
Функция bin() удобна для быстрого перевода чисел в двоичную систему, но при необходимости работы с более сложными форматами, например, с фиксированным количеством разрядов, следует дополнительно использовать методы строк для форматирования.
Реализация собственного алгоритма перевода числа в двоичный формат

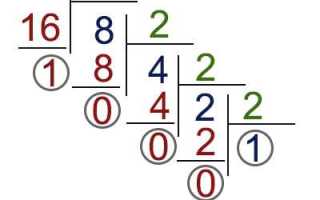
Для перевода числа в двоичную систему можно использовать простой алгоритм деления на 2 с сохранением остатков. Этот процесс позволяет получить представление числа в двоичной системе через последовательность цифр 0 и 1. Алгоритм предполагает деление исходного числа на 2, запись остатка от деления и продолжение до тех пор, пока результат деления не станет равным 0.
Алгоритм выглядит следующим образом:
1. Инициализируем пустую строку для записи двоичного числа. 2. Пока число больше 0: - Находим остаток от деления числа на 2 (это будет следующая цифра двоичного числа). - Добавляем остаток в строку. - Обновляем число, деля его на 2. 3. Разворачиваем строку (потому что остатки записываются в обратном порядке). 4. Получаем результат.
Пример реализации алгоритма на Python:
def decimal_to_binary(n): binary = "" while n > 0: binary = str(n % 2) + binary n = n // 2 return binary
Важно отметить, что алгоритм работает корректно для положительных целых чисел. Для отрицательных чисел можно добавить дополнительную логику обработки, например, через использование дополнительного кода или знаковую мантиссу. Также стоит помнить, что Python предоставляет встроенную функцию bin(), но реализация собственного алгоритма может быть полезной для лучшего понимания работы числовых систем и алгоритмов.
Как обработать отрицательные числа при переводе в двоичную систему
При переводе отрицательных чисел в двоичную систему необходимо учитывать несколько особенностей. В стандартной форме представления чисел на компьютерах используется дополнение до двух (Two's complement), которое позволяет компактно хранить как положительные, так и отрицательные значения. Рассмотрим, как это работает на Python.
Для правильной обработки отрицательных чисел важно понимать, как они кодируются в двоичной системе. В дополнении до двух, отрицательное число представляется как инвертированное (поразрядно) положительное число с последующим увеличением на 1.
Шаги перевода отрицательного числа в двоичную систему:

- Возьмите абсолютное значение числа.
- Переведите его в двоичную систему с помощью стандартных методов.
- Инвертируйте биты (замените все 0 на 1 и наоборот).
- Прибавьте 1 к полученному числу.
def to_binary(n): if n < 0: n = (1 << n.bit_length()) + n return bin(n)[2:]
Этот код корректно преобразует отрицательное число в двоичную систему, применяя дополнение до двух. Также стоит отметить, что при использовании данной функции важно, чтобы битовая длина числа была достаточной для представления в нужной системе счисления.
Пример:
Обратите внимание, что результат будет длинной строкой, где старшие биты представляют знаковую часть числа, а младшие – саму величину.
Для работы с конкретной разрядностью можно указать фиксированную длину строки, например, для 8-битного представления:
def to_binary_fixed(n, bits=8): if n < 0: n = (1 << bits) + n return bin(n)[2:].zfill(bits)
Этот код ограничивает количество разрядов и дополнительно заполняет строку ведущими нулями при необходимости.
Перевод числа с плавающей точкой в двоичную систему

Число с плавающей точкой в двоичной системе представляется в виде двух частей: целой и дробной. Важно понимать, что стандартное представление числа с плавающей точкой, как в формате IEEE 754, использует два компонента: мантиссу и экспоненту. Однако для более простого перевода числа в двоичную систему, можно разделить процесс на две части: целую и дробную часть.
Для перевода целой части числа в двоичную систему используется стандартный метод: деление числа на 2 с сохранением остатка до тех пор, пока результат деления не станет равным 0. Остатки, записанные в обратном порядке, составляют двоичное представление целой части числа.
Для перевода дробной части используется метод умножения на 2. Умножаем дробную часть на 2 и записываем целую часть результата. Далее полученный остаток снова умножается на 2, и процесс повторяется. Это продолжается до тех пор, пока дробная часть не станет равной нулю или пока не достигнем требуемой точности. Если дробная часть не может быть представлена точно в двоичной системе, то происходит округление.
Пример: переведем число 6.25 в двоичную систему. Целая часть 6 в двоичной системе: 6 → 110. Дробная часть 0.25 умножаем на 2, получаем 0.5 (целая часть 0), затем 0.5 умножаем на 2, получаем 1.0 (целая часть 1). Таким образом, двоичное представление числа 6.25 будет: 110.01.
Чтобы получить более точное представление числа с плавающей точкой, необходимо учитывать ограничение точности, которое зависит от используемой библиотеки или платформы. В Python стандартный тип данных float использует 64 бита для хранения числа с плавающей точкой. Это ограничивает точность представления числа, что может привести к ошибкам округления при переведении очень длинных дробных частей.
В Python для перевода числа с плавающей точкой в двоичную строку можно использовать встроенную функцию bin() для целой части и метод умножения для дробной части. В более сложных случаях можно воспользоваться модулем struct для работы с представлением числа с плавающей точкой в формате IEEE 754.
Конвертация числа в двоичный формат с удалением префикса "0b"
Функция bin() в Python возвращает строку, представляющую двоичное представление числа, но с префиксом 0b. Чтобы получить только бинарные цифры, необходимо удалить первые два символа строки.
Для этого можно воспользоваться срезом строки:
n = 37
binary = bin(n)[2:]
Альтернативный способ – использовать функцию format() с форматом 'b', который сразу возвращает двоичное представление без префикса:
n = 37
binary = format(n, 'b')
При необходимости дополнить результат ведущими нулями до заданной длины, можно использовать метод zfill():
n = 5
binary = format(n, 'b').zfill(8)
Для получения двоичного представления числа в строковом формате используется встроенная функция format() с шаблоном 'b'. Пример: format(13, 'b') вернёт строку '1101'.
Альтернативный способ – f-строки. Запись f"{13:b}" даёт тот же результат. Этот метод удобен при форматировании строк с несколькими переменными.
Для выравнивания и заполнения нулями используется модифицированный формат. Пример: format(5, '08b') возвращает '00000101'. Здесь 08 означает ширину 8 символов с ведущими нулями.
Для форматирования нескольких чисел одинаковой ширины удобно использовать генераторы: [format(x, '04b') for x in range(4)] создаст список ['0000', '0001', '0010', '0011'].
Вопрос-ответ: