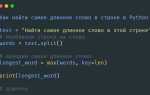
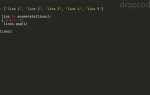
Арктангенс – это обратная функция для тангенса, которая используется для нахождения угла, если известна его тангенс. В Python для вычисления арктангенса можно воспользоваться встроенной функцией atan() из библиотеки math, которая возвращает результат в радианах. Если вам необходим результат в градусах, его можно преобразовать с помощью константы pi и стандартной формулы.
Функция atan() принимает один аргумент – число, которое является значением тангенса угла. Результат вычисления ограничен диапазоном от -π/2 до π/2. Это важно учитывать, поскольку арктангенс определен только для чисел, которые могут быть тангенсами углов, т.е. для всех действительных чисел.
Для получения результата в градусах следует использовать формулу: угол (в градусах) = atan(x) * (180 / pi), где x – это значение, для которого требуется вычислить арктангенс. Также можно воспользоваться функцией degrees() из той же библиотеки math, чтобы автоматизировать преобразование радианов в градусы.
Как вычислить арктангенс с помощью Python
Пример использования:
import math
# Вычисление арктангенса
x = 1
result = math.atan(x)
print(result)Функция math.atan(x) возвращает результат в радианах. Если требуется получить угол в градусах, можно воспользоваться функцией math.degrees(), которая преобразует радианы в градусы:
import math
x = 1
result_radians = math.atan(x)
result_degrees = math.degrees(result_radians)
print(result_degrees)Таким образом, для вычисления арктангенса числа в Python достаточно выполнить следующие шаги:
- Импортировать библиотеку
math. - Вызвать функцию
math.atan(x), гдеx– это число, для которого нужно найти арктангенс. - Если нужно, преобразовать результат из радианов в градусы с помощью
math.degrees().
Для вычисления арктангенса можно использовать и другие подходы, например, с помощью библиотеки numpy, если требуется работать с массивами данных.
import numpy as np
x = np.array([1, 2, 3])
result = np.arctan(x)
print(result)Функция np.arctan() работает аналогично math.atan(), но может сразу возвращать арктангенс для нескольких значений в виде массива.
Как использовать функцию atan() из библиотеки math
Для того чтобы использовать atan(), необходимо сначала импортировать библиотеку math:
import mathПример использования функции:
result = math.atan(1)
print(result)В данном примере функция atan(1) вернет значение, которое соответствует углу в радианах для тангенса, равного 1. Это примерно 0.7853981633974483, что соответствует π/4.
Функция atan() принимает один аргумент – значение, для которого требуется вычислить арктангенс. Аргумент должен быть числом (целым или с плавающей точкой). Вернувшееся значение – это угол в радианах. Чтобы перевести результат в градусы, можно воспользоваться функцией degrees() из той же библиотеки:
degrees_result = math.degrees(result)
print(degrees_result)Такой подход позволяет легко работать с углами в градусах. Результат будет примерно равен 45.0 градусов.
Важно отметить, что atan() всегда возвращает значение для углов, находящихся в первой или четвертой четверти (от -π/2 до π/2). Для получения углов в других четвертях можно использовать функцию atan2().
Как рассчитать арктангенс для разных типов данных

Арктангенс можно вычислять для различных типов данных в Python, включая целые числа, числа с плавающей точкой и даже массивы данных. Рассмотрим основные способы работы с арктангенсом для разных типов данных.
Для расчета арктангенса в Python используется функция atan() из библиотеки math. Она принимает одно числовое значение и возвращает арктангенс этого числа в радианах. Например:
import math
result = math.atan(1)
print(result) # Выведет 0.7853981633974483Арктангенс чисел с плавающей точкой и целых чисел работает одинаково. Однако важно учитывать точность значений, так как числа с плавающей точкой могут иметь погрешности, особенно при работе с большими или малыми числами.
При работе с массивами данных, например, с помощью библиотеки numpy, можно рассчитать арктангенс для целых массивов чисел за один вызов функции atan(). Это эффективно для обработки больших данных:
import numpy as np
data = np.array([1, 2, 3, 4, 5])
result = np.arctan(data)
print(result) # Выведет массив значений арктангенсов для каждого элементаДля комплексных чисел используется функция atan() из библиотеки cmath. Для комплексных чисел результат будет комплексным числом, где действительная часть – это арктангенс модуля числа, а мнимая часть – аргумент:
import cmath
complex_number = 1 + 1j
result = cmath.atan(complex_number)
print(result) # Выведет комплексное числоАрктангенс можно также вычислять для углов в градусах, конвертируя результат из радианов в градусы с помощью функции degrees() из библиотеки math:
angle_in_degrees = math.degrees(result)
print(angle_in_degrees) # Конвертирует результат в градусыТаким образом, расчет арктангенса зависит от типа данных, с которыми работает программа. Важно выбирать подходящий метод в зависимости от того, нужно ли работать с числами в радианах, градусах или комплексных значениях.
Как вычислить арктангенс для угла в градусах
Для вычисления арктангенса угла в градусах, сначала необходимо воспользоваться функцией atan из библиотеки math в Python. Однако эта функция возвращает результат в радианах. Чтобы преобразовать результат в градусы, нужно использовать функцию degrees из той же библиотеки.
Пример кода:
import math # Угол в радианах radians = math.atan(1) # Преобразование в градусы degrees = math.degrees(radians) print(degrees)
В данном примере вычисляется арктангенс числа 1, результат которого равен 45 градусам, так как арктангенс 1 – это угол 45 градусов. Важно помнить, что результат функции atan всегда лежит в пределах от -π/2 до π/2 радиан, что соответствует углам от -90 до 90 градусов.
Если нужно вычислить арктангенс для других значений, замените аргумент функции atan на нужное число. Например, для чисел меньше 0 результат будет отрицательным, что соответствует углам в нижней половине координатной плоскости.
Как получить арктангенс с учетом диапазона значений
Функция арктангенса, или atan, по умолчанию возвращает угол в диапазоне от -π/2 до π/2. Этот результат соответствует обратному отношению между координатами на единичной окружности для значений от минус бесконечности до плюс бесконечности. Однако в некоторых задачах требуется учитывать весь круг – от -π до π, чтобы точно понять, в какой четверти находится угол. Для этого используется функция atan2(y, x).
Функция atan2(y, x) принимает два аргумента: координаты точки (x, y). Она вычисляет арктангенс с учетом знаков обоих аргументов, возвращая угол в диапазоне от -π до π. Это важно для задач, где необходимо учитывать направление и точное расположение точки на плоскости.
Пример использования atan2 в Python:
import math
y = 1
x = 1
angle = math.atan2(y, x)
print(angle) # 0.7853981633974483 (π/4)В этом примере, при (x=1, y=1), функция atan2 вернет значение, соответствующее углу 45 градусов или π/4. Важно, что в случае различных знаков x и y, atan2 учтет их правильное расположение на координатной плоскости.
Если необходимо получить значение арктангенса в другом диапазоне, например, от 0 до 2π, можно добавить условие для преобразования результата, умножив его на 2 и добавив π для значений, которые изначально возвращаются отрицательными.
Как вычислить арктангенс для комплексных чисел в Python
В Python для работы с комплексными числами используется модуль cmath, который предоставляет функции для различных математических операций, включая арктангенс для комплексных чисел.
Арктангенс для комплексных чисел вычисляется с помощью функции cmath.atan(z), где z – комплексное число. Эта функция возвращает комплексный результат, представляющий арктангенс числа. Формула для арктангенса комплексного числа имеет вид:
$$ \text{atan}(z) = \frac{i}{2} \ln \left( \frac{i+z}{i-z} \right) $$
Для примера, чтобы вычислить арктангенс комплексного числа, достаточно передать его в функцию atan:
import cmath
z = complex(1, 1)
result = cmath.atan(z)
print(result)В этом примере арктангенс комплексного числа 1 + 1j будет вычислен и выведен на экран. Результат будет комплексным числом, в котором действительная и мнимая части могут быть интерпретированы как углы и длины для соответствующего комплексного числа.
Если передать в atan число на мнимой оси, например 1j, результатом будет чисто мнимое значение. Также стоит учитывать, что арктангенс комплексных чисел имеет многозначность, что обусловлено особенностями комплексных чисел и периодичностью функций логарифма и арктангенса.
Важно помнить, что результат работы cmath.atan(z) соответствует значению угла, который образует комплексное число с положительной действительной осью в комплексной плоскости.
Как интерпретировать результат функции atan() и использовать его в расчетах

Функция math.atan(x) возвращает арктангенс аргумента x в радианах. Диапазон результата – от -π/2 до π/2. Значение соответствует углу в прямоугольном треугольнике с отношением противолежащего катета к прилежащему, равным x.
Для перевода результата в градусы используйте:
import math угол_в_градусах = math.degrees(math.atan(x))
Функция atan() применяется при расчёте угла наклона, направления векторов и преобразования координат. Например, при определении угла между двумя точками на плоскости:
dx = x2 - x1 dy = y2 - y1 угол = math.atan2(dy, dx) # учитывает четверть координатной плоскости
math.atan2() предпочтительнее при работе с координатами, так как результат охватывает диапазон от -π до π и корректно определяет направление вектора относительно оси X.
При расчётах с использованием результата atan() учитывайте, что тригонометрические функции в Python работают в радианах. Для дальнейших вычислений, например векторных проекций, оставляйте результат в радианах. Для визуализации – переводите в градусы.
Избегайте передачи значений, близких к бесконечности, в atan(), чтобы не получить пограничные значения ±π/2, которые могут искажать интерпретацию при обратных преобразованиях.