Matlab и Mathcad – это два мощных инструмента для математического моделирования, анализа данных и решения инженерных задач. Они применяются в научных исследованиях, проектировании и разработке алгоритмов. Несмотря на схожесть в предназначении, их функциональность, интерфейс и области применения существенно различаются.
Matlab – это среда разработки для численных вычислений и алгоритмического моделирования. Основанный на языке программирования MATLAB, он предоставляет широкие возможности для анализа больших объемов данных, создания математических моделей и проведения симуляций. Он наиболее эффективно используется для работы с линейной алгеброй, обработкой сигналов и изображений, а также в области машинного обучения и искусственного интеллекта. В Matlab вы работаете с кодом, что дает гибкость в реализации сложных вычислений и интеграции с другими системами.
Mathcad – это инструмент для решения инженерных задач с акцентом на визуализацию и документирование расчетов. В отличие от Matlab, Mathcad предлагает интуитивно понятный интерфейс с возможностью вводить математические выражения в привычной для инженера и ученого форме, что делает его удобным для работы с формулами. Основное преимущество Mathcad – это возможность создания живых документов, которые автоматически обновляются при изменении исходных данных. Mathcad более ориентирован на пользователей, которым нужно быстро решить задачу и получить понятный результат.
Использование Matlab и Mathcad зависит от конкретных задач. Matlab подходит для сложных расчетов, требующих программирования и работы с большими данными. Mathcad идеален для документирования процессов и получения быстрых решений с фокусом на презентацию. Важно выбирать инструмент, который будет наиболее эффективным для вашего проекта, с учетом необходимой гибкости и визуализации данных.
Как начать работу в Matlab: установка и первые шаги
Для начала работы с Matlab необходимо установить программное обеспечение. Для этого нужно перейти на официальный сайт MathWorks и выбрать подходящую версию для вашей операционной системы. Matlab доступен для Windows, macOS и Linux. При установке потребуется учетная запись MathWorks. Если у вас её нет, создайте её на сайте компании.
1. Установка Matlab: После скачивания установочного файла следуйте инструкциям на экране. Выберите компоненты, которые хотите установить. Для большинства пользователей достаточно базового набора, включающего основные функции, Simulink и поддержу для работы с графикой.
2. Активация Matlab: После завершения установки нужно активировать программу, введя лицензионный ключ, который предоставляется при покупке. Если у вас нет ключа, вы можете воспользоваться бесплатной пробной версией, которая доступна на сайте MathWorks.
3. Основной интерфейс: После запуска Matlab откроется главное окно с несколькими разделами: командное окно (Command Window), редактор скриптов (Editor), и рабочее пространство (Workspace). Командное окно предназначено для ввода и выполнения команд, редактор скриптов – для написания и сохранения программ, а рабочее пространство отображает все переменные, используемые в текущей сессии.
4. Первые шаги: Введите простое выражение в командном окне, например, 2 + 2, и нажмите Enter. Matlab выполнит расчет и отобразит результат. Это простое действие позволяет убедиться в правильности работы программы.
Для выполнения более сложных задач можно создать скрипт. Откройте редактор скриптов, напишите код, например, для создания графика функции, и сохраните его с расширением .m. Запустите скрипт, чтобы увидеть результат. Пример скрипта для построения графика синуса:
Пример:
x = 0:0.1:10;
y = sin(x);
plot(x, y);
title('График функции sin(x)');
xlabel('x');
ylabel('sin(x)');
5. Документация и помощь: Matlab имеет встроенную документацию. Для получения информации о функции введите help перед её именем в командном окне, например, help plot. Это откроет описание и примеры использования функции.
После выполнения этих шагов вы будете готовы к более сложным вычислениям и анализам в Matlab. Важно также регулярно сохранять скрипты и следить за правильностью синтаксиса, так как Matlab может не всегда дать явную ошибку, если код не соответствует его стандартам.
Основные функции Mathcad для решения инженерных задач
Mathcad предлагает набор мощных инструментов для решения инженерных задач, обеспечивая простоту использования и высокую гибкость в обработке данных. Среди ключевых функций, которые делают его эффективным инструментом для инженеров, выделяются:
Решение математических уравнений. Mathcad позволяет решать как простые, так и сложные системы уравнений, используя как символическое, так и численное решение. Это позволяет легко находить корни уравнений, оптимизировать параметры и решать нелинейные системы. Пример использования: для оптимизации конструкции можно задать систему уравнений, учитывающую различные параметры (например, размеры, нагрузку, прочность), и получить сразу несколько вариантов решений.
Численные методы и интеграция. Mathcad обладает встроенными функциями для численного интегрирования, дифференцирования и решения дифференциальных уравнений. Эти методы полезны, когда аналитическое решение невозможно или слишком сложное для получения вручную. Например, интеграция функций температуры по времени для расчета тепловых процессов или численное решение дифференциальных уравнений движения для моделирования динамики системы.
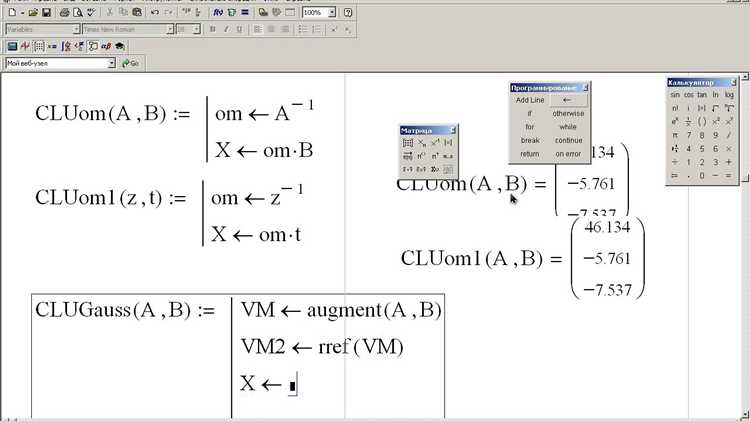
Работа с матрицами и векторами. Для инженеров, работающих с системами линейных уравнений или матричными операциями, Mathcad предоставляет удобный интерфейс для работы с матрицами. Это важная функция при решении задач механики, электротехники, оптимизации и других областей. Использование матричных операций позволяет значительно упростить решение многомерных задач, таких как расчет напряжений в конструкции или распределение потоков энергии в сетях.
Графическое отображение данных. Mathcad позволяет строить графики функций, диаграммы, и визуализировать данные для лучшего понимания и анализа результатов. В инженерных расчетах это особенно важно для оценки поведения системы в разных условиях или для визуализации зависимости между различными параметрами, например, зависимость давления от температуры в теплообменном процессе.
Символьные вычисления. Mathcad имеет встроенную поддержку символьных вычислений, что позволяет манипулировать алгебраическими выражениями, дифференцировать и интегрировать их аналитически. Эта функция полезна, когда нужно получить точное аналитическое решение для сложных уравнений, например, при расчете жесткости конструкции или силовых характеристик системы.
Интерактивность и создание отчетов. Одной из сильных сторон Mathcad является возможность создания интерактивных документов, в которых можно изменять параметры и сразу видеть результаты расчетов. Это позволяет не только автоматизировать процесс расчетов, но и создавать документацию, которая будет полезна в процессе проектирования, позволяя коллегам или заказчикам взаимодействовать с расчетами напрямую.
Библиотеки и встроенные функции. Mathcad включает в себя богатую библиотеку стандартных функций и инструментов для инженерных расчетов, таких как расчет механических свойств материалов, термодинамических процессов, электрических цепей и многих других. Библиотеки значительно ускоряют решение типовых инженерных задач и гарантируют точность вычислений.
Использование этих функций позволяет инженерам сократить время на решение задач, повысить точность расчетов и улучшить качество проектирования, предоставляя удобный интерфейс для работы с данными и результатами.
Сравнение Matlab и Mathcad: когда использовать каждый инструмент

Matlab и Mathcad – два популярных инструмента для математического моделирования, но их использование сильно зависит от задач. Оба предоставляют мощные возможности, но имеют принципиальные различия в подходах и интерфейсах.
Matlab является мощной средой для численных расчетов и программирования, ориентированной на инженеров, ученых и разработчиков. Его основное преимущество – это гибкость и возможность создания сложных алгоритмов, анализа больших данных и работы с матричными вычислениями. В то время как Mathcad чаще используется для решения стандартных инженерных задач с упором на визуализацию и математическую документацию.
Когда использовать Matlab:
- Для сложных численных методов: Matlab хорошо справляется с вычислениями, которые требуют большого объема данных или требуют специфических математических моделей, таких как решение дифференциальных уравнений, оптимизация или симуляция систем.
- Для разработки алгоритмов: Matlab поддерживает программирование и разработку алгоритмов с возможностью работы с большими массивами данных, использованием внешних библиотек и созданием кастомизированных функций.
- Для анализа и визуализации данных: В Matlab мощные инструменты для визуализации, которые подходят для разработки сложных графиков и 3D-моделей. Это важно при анализе больших объемов данных, где стандартные инструменты не могут предоставить нужную гибкость.
Когда использовать Mathcad:
- Для инженерных расчетов: Mathcad идеально подходит для создания подробных отчетов по инженерным расчетам, где важна наглядность и документированность каждого шага. В нем можно легко описать формулы и добавить пояснения, создавая подробную математическую документацию.
- Для решения стандартных задач: Mathcad подходит для быстрого решения стандартных математических задач, таких как линейная алгебра, вычисления для механики, электротехники и других инженерных дисциплин.
- Для образовательных целей: Mathcad проще в освоении, имеет более интуитивно понятный интерфейс и позволяет сосредоточиться на математических расчетах без необходимости погружаться в сложное программирование.
Как работать с матрицами и векторами в Matlab
Чтобы создать вектор в Matlab, достаточно ввести его в командной строке. Например, для строки из чисел можно использовать следующую команду:
x = [1 2 3 4 5];
Для столбцового вектора элементы разделяются точкой с запятой:
y = [1; 2; 3; 4; 5];
Матрицы создаются аналогично. Например, для матрицы 2×3 можно ввести:
A = [1 2 3; 4 5 6];
Здесь символ «;» разделяет строки, а пробелы – элементы в строках. Matlab автоматически определяет размерность массива по введенным данным.
Операции над матрицами и векторами в Matlab поддерживают стандартные линейные алгебраические правила. Для сложения или вычитания матриц необходимо, чтобы их размеры совпадали. Например:
C = A + B;
Где A и B – матрицы одинакового размера. Для умножения матриц используется оператор «*», но важно помнить, что умножение возможно только если число столбцов первой матрицы равно числу строк второй.
Для работы с элементами матрицы или вектора используются индексы. В Matlab индексация начинается с единицы. Чтобы обратиться к элементу, например, ко второму элементу вектора x, нужно использовать:
x(2)
Или к элементу матрицы в строке 2, столбце 3:
A(2,3)
Для выполнения операций поэлементно (например, сложение, умножение, деление) нужно использовать точку перед оператором. Например:
C = A .* B;
Эта операция произведет поэлементное умножение матриц A и B.
Для транспонирования матрицы используется оператор апостроф (‘). Например:
A' % транспонированная матрица
Функции Matlab для работы с векторами и матрицами включают:
- size(A) – возвращает размеры матрицы A;
- length(x) – возвращает длину вектора x;
- det(A) – определитель матрицы;
- inv(A) – обратная матрица;
- rank(A) – ранг матрицы;
- eig(A) – собственные значения и векторы матрицы A.
Для выполнения более сложных математических операций и алгоритмов, таких как решение линейных систем, оптимизация или анализ данных, Matlab имеет готовые функции, которые значительно упрощают код.
Таким образом, для эффективной работы с матрицами и векторами в Matlab достаточно освоить основные операции и функции, а также понимать структуру данных, что позволяет быстро решать математические задачи.
Создание и решение уравнений в Mathcad
Mathcad предоставляет удобные инструменты для работы с уравнениями. В этом программном обеспечении можно не только записывать математические выражения в привычной для инженера и ученого форме, но и решать их с помощью встроенных функций.
Основной инструмент для решения уравнений в Mathcad – это оператор «решения». Он позволяет работать как с простыми линейными уравнениями, так и с более сложными нелинейными или дифференциальными.
Для создания уравнений в Mathcad достаточно просто ввести выражение в поле документа. Например, чтобы записать уравнение типа «a * x + b = 0», нужно ввести:
- a * x + b = 0
После того как уравнение записано, можно воспользоваться функцией решения. Для этого можно использовать команду solve или воспользоваться более простым методом: ввести переменную, например, x := solve(a * x + b = 0, x), где a * x + b = 0 – это уравнение, а x – неизвестная переменная.
Mathcad автоматически решит уравнение относительно переменной x. В случае с более сложными уравнениями, как например, с дифференциальными уравнениями, Mathcad предложит соответствующие инструменты для их решения.
Пример решения дифференциального уравнения:
- dy/dx = x * y
Для нахождения решения можно ввести уравнение как:
- d(y(x), x) = x * y(x)
После этого Mathcad предложит решение, которое будет отображаться в аналитической форме, если решение существует в явном виде. В противном случае будет предложен численный метод решения.
Кроме того, Mathcad позволяет работать с системой уравнений. Для этого достаточно ввести систему как несколько уравнений, разделенных точками с запятой или новой строкой, и решить их одновременно. Например:
- a * x + b = 0;
- c * x + d = 5
Для нахождения значений переменных x, можно использовать команду solve с указанием всех уравнений в системе.
Таким образом, создание и решение уравнений в Mathcad – это интуитивно понятный процесс, который позволяет значительно ускорить расчеты и повысить точность работы с математическими моделями.
Использование графиков и визуализаций в Matlab
Команда plot является основой для построения двумерных графиков. Например, чтобы построить график функции y = sin(x), нужно выполнить следующее:
x = 0:0.1:10; y = sin(x); plot(x, y);
Для улучшения визуализации графика можно добавлять метки осей с помощью команды xlabel и ylabel, а также заголовок с помощью title.
xlabel('x');
ylabel('y');
title('График функции y = sin(x)');
Если необходимо построить график нескольких функций на одном рисунке, используется команда hold on, которая позволяет добавлять новые графики без очистки предыдущих. Например:
plot(x, sin(x));
hold on;
plot(x, cos(x));
legend('sin(x)', 'cos(x)');
Для представления данных в виде точек используется команда scatter. Она полезна, например, для отображения зависимости между двумя переменными в виде рассеянных точек:
scatter(x, y);
Для более сложных визуализаций, например, 3D-графиков, используется функция surf, которая позволяет отображать поверхность. Для примера:
[X, Y] = meshgrid(-5:0.5:5, -5:0.5:5); Z = X.^2 + Y.^2; surf(X, Y, Z);
Особенностью Matlab является возможность интеграции графиков с другими инструментами, такими как анимации или динамические графики. Для создания анимаций можно использовать функцию plot3 в сочетании с циклом for, что позволяет визуализировать изменение данных в реальном времени. Пример кода для анимации:
x = linspace(0, 2*pi, 100); y = sin(x); h = plot(x, y); for t = 1:length(x) y = sin(x + t/10); set(h, 'YData', y); pause(0.05); end
Также Matlab поддерживает экспорт графиков в различные форматы, включая PNG, EPS и PDF, что позволяет интегрировать визуализации в отчеты и презентации. Для этого используется команда saveas:
saveas(gcf, 'plot.png');
Таким образом, Matlab предоставляет мощный набор инструментов для создания как простых, так и сложных графиков, а также для их интеграции с расчетами и моделями, что делает его незаменимым инструментом в научных и инженерных исследованиях.
Автоматизация расчетов с помощью скриптов в Matlab и Mathcad
Автоматизация расчетов в Matlab и Mathcad позволяет значительно ускорить процесс решения инженерных и научных задач, повышая точность и исключая человеческие ошибки. Оба инструмента предоставляют пользователям возможность писать скрипты, что открывает широкие возможности для повторного использования и улучшения рабочих процессов.
В Matlab скрипты представляют собой текстовые файлы с расширением .m, содержащие последовательность команд для выполнения операций. Скрипты могут включать в себя вычисления, построение графиков, работу с массивами данных и даже создание пользовательских функций. Важно, что скрипты Matlab позволяют интегрировать внешние библиотеки и использовать встроенные пакеты для решения задач из различных областей науки и техники. С помощью скриптов можно автоматизировать как простые вычисления, так и сложные многократные симуляции.
Пример автоматизации с помощью скрипта в Matlab:
Предположим, необходимо решить систему линейных уравнений для различных наборов данных. Вместо того чтобы каждый раз вводить данные вручную, можно создать скрипт:
A = [3 2; 4 5]; B = [7; 10]; X = linsolve(A, B); disp(X);
Этот скрипт автоматически решит систему линейных уравнений, и результат можно будет вывести в консоль, а также сохранить в файл для дальнейшего анализа. При этом процесс можно повторить для разных наборов значений A и B, что ускоряет выполнение задачи.
В Mathcad автоматизация расчетов происходит через создание «расчетных листов», которые содержат как текстовые пояснения, так и математические выражения, напрямую связанные с результатами вычислений. В Mathcad особое внимание уделено визуализации данных, и любые изменения, сделанные в расчетах, немедленно отображаются на графиках и в таблицах. Скрипты в Mathcad могут включать пользовательские функции, которые позволяют повторно использовать блоки кода для решения аналогичных задач.
Пример автоматизации в Mathcad:
Для решения того же задания, связанного с системой линейных уравнений, в Mathcad достаточно ввести выражение:
A := [[3, 2], [4, 5]] B := [7, 10] X := A^-1 * B
Mathcad автоматически выполнит вычисления и отобразит результат в виде вектора X. Пользователь может легко изменять матрицы и наблюдать, как изменяется решение. Важно, что каждый расчет можно сохранить в виде документа, и в будущем легко повторить его, изменив лишь исходные данные.
Рекомендации:
- Для ускорения работы с большими объемами данных в Matlab используйте векторизацию, избегая использования циклов там, где это возможно.
- В Mathcad используйте возможности автоматического обновления расчетов, чтобы в любой момент времени иметь актуальные результаты при изменении входных параметров.
- Обязательно применяйте функции и модули для повторных вычислений, чтобы избежать дублирования кода и ошибок в расчетах.
Таким образом, автоматизация расчетов с помощью скриптов в Matlab и Mathcad позволяет не только ускорить рабочий процесс, но и повысить точность выполнения задач, обеспечив большую гибкость и удобство при работе с математическими моделями.
Вопрос-ответ:
Что такое Matlab и как его использовать?
Matlab — это программное обеспечение для численных вычислений, анализа данных, визуализации и разработки алгоритмов. Он широко используется в науке, инженерии и экономике для решения математических задач. Основное преимущество Matlab — его удобный синтаксис и богатый набор встроенных функций. В Matlab можно решать линейные уравнения, проводить статистические исследования, строить графики и многое другое. Для работы с Matlab достаточно изучить основы его командного интерфейса и научиться писать скрипты, которые автоматизируют различные вычисления.
В чем отличие Matlab от Mathcad?
Основное отличие между Matlab и Mathcad заключается в их подходе к решению задач. Matlab больше ориентирован на программирование и автоматизацию вычислений. Это мощная среда для работы с большими массивами данных и сложными алгоритмами. В отличие от этого, Mathcad предоставляет более визуальный подход: вы можете вводить математические выражения прямо в формулах и они сразу рассчитываются. Mathcad идеален для тех, кто хочет документировать свои расчеты и работать с математическими формулами в удобной, почти «ручной» манере, тогда как Matlab подходит для более сложных и масштабных вычислений.
Какие преимущества у Mathcad для инженеров и научных работников?
Mathcad позволяет интегрировать текст и математические формулы в одном документе, что очень удобно для инженеров и научных работников, которым необходимо представлять свои расчеты с пояснениями. В Mathcad легко решать уравнения, выполнять численные вычисления и интегрировать результаты в отчеты. Программное обеспечение позволяет работать с единицами измерений и автоматически конвертировать их, что упрощает расчет и анализ данных. Mathcad идеально подходит для тех, кто нуждается в быстром и понятном способе документирования своих инженерных решений.
Можно ли использовать Matlab для решения задач в области искусственного интеллекта?
Да, Matlab обладает множеством встроенных функций и инструментов, которые позволяют решать задачи в области искусственного интеллекта (ИИ). В частности, в Matlab есть инструменты для работы с нейронными сетями, машинным обучением, обработкой изображений и другими задачами ИИ. Для начала работы с ИИ в Matlab можно использовать встроенную библиотеку `Deep Learning Toolbox`, которая предоставляет функции для создания и обучения нейронных сетей. Это позволяет решать задачи классификации, регрессии, а также выполнять обработку изображений и текста.
Что такое Matlab и Mathcad, и в чем их отличие?
Matlab и Mathcad — это два мощных инструмента для работы с математическими расчетами, моделированием и аналитическими задачами. Matlab, в первую очередь, используется для выполнения численных расчетов, обработки данных и визуализации. Это язык программирования с огромным количеством встроенных функций и библиотек, что делает его универсальным инструментом для ученых и инженеров. Mathcad, с другой стороны, представляет собой программное средство для решения инженерных задач и математических расчетов с акцентом на визуальное представление решений. Он удобен для построения расчетных схем и диаграмм, а также для документирования решения задач. Главным различием является то, что Matlab требует знаний программирования, а Mathcad ориентирован на более визуальный подход с минимальной необходимостью кодирования.