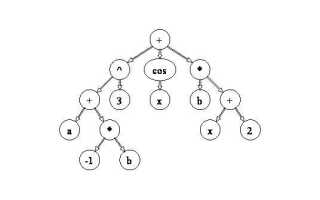
Как упростить выражение в maple

Maple предоставляет мощные инструменты для работы с алгебраическими выражениями, позволяя сократить сложные формулы и упростить вычисления. В основе упрощения лежат функции simplify, expand и factor, каждая из которых решает конкретные задачи и требует правильного применения для достижения оптимального результата.

При работе с выражениями в Maple важно понимать, какие операции выполняет каждая функция и в каком порядке их использовать. Например, предварительное разложение на множители может значительно ускорить последующее упрощение. Также стоит учитывать настройки параметров функции simplify, которые позволяют уточнять критерии упрощения, например, сведение к рациональной форме или сокращение тригонометрических выражений.

Это руководство детально разберет последовательность действий с примерами команд, которые помогут быстро и эффективно преобразовать исходные формулы в более компактный и удобочитаемый вид. Специализированные приемы, включающие работу с подстановками и автоматическую проверку эквивалентности выражений, позволят повысить точность и экономию времени при вычислениях в Maple.

Настройка окружения Maple для работы с упрощением выражений

Перед началом упрощения выражений в Maple важно правильно настроить рабочее пространство, чтобы повысить эффективность и точность вычислений.

Выбор пакетов и библиотек. Убедитесь, что загружен пакет Student[Calculus1] или Student[Algebra], так как они содержат необходимые функции для упрощения. Команда для загрузки: with(Student[Calculus1]): или with(Student[Algebra]):.

Настройка точности вычислений. Для числовых выражений используйте команду Digits := 15: для повышения точности и предотвращения ошибок округления при упрощении.

Оптимизация параметров упрощения. В Maple доступны функции с аргументом steps для контроля уровня детализации упрощения. Например, simplify(expr, steps=3); позволит видеть промежуточные этапы преобразования.

Выбор вида упрощения. Используйте команды simplify, combine, expand в зависимости от цели: simplify для общего упрощения, combine – для объединения дробей или логарифмов, expand – для раскрытия скобок.

Установка ограничений на упрощение. Включайте или отключайте использование тригонометрических или логарифмических преобразований через параметры команды, например, simplify(expr, trig=false); для запрета тригонометрического упрощения.

Автоматизация процесса. Создавайте скрипты с последовательностью команд упрощения для повторного использования и снижения ошибок. Это особенно полезно при работе с большими выражениями.

Использование команды simplify для базового упрощения алгебраических выражений

Команда simplify в Maple предназначена для приведения выражений к более компактной и удобочитаемой форме без изменения их математического смысла. Она автоматически применяет основные алгебраические преобразования, такие как сокращение дробей, раскрытие скобок и упрощение степеней.

Рекомендации по работе с simplify:

Для базового упрощения достаточно вызвать simplify(expr);, где expr – исходное выражение.
Команда корректно обрабатывает рациональные выражения, алгебраические дроби и полиномы.
При упрощении тригонометрических и экспоненциальных выражений simplify действует по умолчанию ограниченно, для более глубокого упрощения нужны дополнительные параметры.
Используйте simplify(expr, assume), чтобы задать условия упрощения, например, simplify(expr, assume = x > 0); для выражений с ограничениями на переменные.
Команда не меняет структуру выражения радикалов и не раскрывает сложные формулы без специальных опций.

Пример базового упрощения:

expr := (x^2 - 1)/(x - 1);
simplify(expr);

Результат будет x + 1, так как x^2 - 1 разлагается на множители, а x - 1 сокращается.

При работе с большими выражениями simplify помогает быстро избавиться от очевидных избыточных компонентов, что упрощает дальнейший анализ и вычисления.

Применение функций expand и factor для преобразования многочленов

В Maple функции expand и factor выполняют обратные операции, позволяя преобразовывать многочлены для удобства последующих вычислений. expand раскрывает скобки и приводит выражение к форме суммы одночленов. Например, выражение (x + 2)*(x - 3) после применения expand преобразуется в x^2 - x - 6. Это упрощает операции сложения, интегрирования и дифференцирования.

Функция factor осуществляет разложение многочлена на множители. Её используют для поиска корней, сокращения дробей и анализа структуры выражения. Например, factor(x^2 - x - 6) вернёт (x - 3)*(x + 2). Для многочленов с несколькими переменными полезно применять factor с дополнительными параметрами, например, factor(expr, extension = {I}) для комплексных корней.

При работе с функциями важно следить за типом исходного выражения: если оно не является многочленом, результат может быть неожиданным. Рекомендуется сначала использовать expand для раскрытия скобок, затем factor для разложения. Для контроля промежуточных результатов удобно сохранять выражения в переменные.

Автоматизация процесса достигается через вложенные вызовы, например, factor(expand(expr)), что позволяет одновременно раскрыть скобки и разложить полученный многочлен. При работе с большими выражениями следует учитывать производительность: expand может значительно увеличить размер выражения, что влияет на время вычислений.

В случаях, когда нужно разложить выражение только по определённой переменной, используется параметр factor(expr, x), что ускоряет работу и даёт более релевантный результат. Также полезна функция simplify для комбинирования эффектов expand и factor, но при этом требуется понимать, какую форму результата нужно получить.

Упрощение дробных выражений и рациональных функций в Maple

Для упрощения дробных выражений в Maple применяется команда simplify с опцией symbolic, которая позволяет минимизировать числитель и знаменатель. Например, выражение simplify((x^2 - 1)/(x^2 - x)) автоматически сокращается до (x+1)/x.

Если требуется более глубокое разложение, полезна функция factor, позволяющая разложить числитель и знаменатель на множители перед сокращением. Например, factor((x^2 - 1)/(x^2 - x)) выделит множители, что облегчит последующее сокращение.

Для рациональных функций с параметрами рекомендовано использовать simplify в сочетании с assume, задавая ограничения на переменные. Это предотвращает ошибочные упрощения, например, при делении на ноль. Пример: assume(x <> 0); simplify((x^2 - 1)/(x^2 - x));.

В случаях, когда стандартное упрощение не приводит к нужному виду, рекомендуется применить convert с параметрами normal или rational. Это преобразует выражение к дробно-рациональной форме, упрощая вычисления и последующий анализ.

Для упрощения рациональных функций с несколькими переменными и более сложными структурами стоит использовать функцию collect, которая собирает выражение по выбранным переменным, облегчая чтение и анализ результата.

Методы упрощения тригонометрических выражений с помощью trigreduce и trigexpand

В Maple функции trigreduce и trigexpand служат для трансформации тригонометрических выражений с целью упрощения и приведения к более удобной форме. Их применение зависит от структуры исходного выражения и конечной задачи.

trigreduce – сведение произведений и степеней тригонометрических функций к суммам или разностям. Полезна для упрощения сложных произведений и преобразования выражений к линейной комбинации базовых функций.
- Синтаксис: trigreduce(expr), где expr – тригонометрическое выражение.
- Пример: trigreduce(sin(x)^2 * cos(x)) преобразует произведение в сумму или разность синусов и косинусов.
- Рекомендуется применять при наличии степеней тригонометрических функций или сложных произведений.
trigexpand – раскрытие сложных тригонометрических функций, например, двойных аргументов или суммы аргументов, в виде суммы простых тригонометрических функций.
- Синтаксис: trigexpand(expr).
- Пример: trigexpand(sin(2*x)) преобразует к 2*sin(x)*cos(x).
- Эффективна при необходимости раскрыть сложные аргументы для дальнейших упрощений или интегрирования.

Оптимальная последовательность действий:

Для выражений с произведениями и степенями сначала примените trigreduce – это позволит упростить структуру выражения и снизить количество перемножаемых функций.
Если в выражении присутствуют функции с составными аргументами (например, sin(3*x) или cos(x+y)), используйте trigexpand для раскрытия этих аргументов в суммы или разности.
После раскрытия аргументов возможно повторное применение trigreduce для минимизации получившихся выражений.

Дополнительно, для повышения эффективности упрощения рекомендуется:

Комбинировать с командой simplify(expr, trig), которая применяет встроенные тригонометрические упрощения.
Использовать eval(expr, trig) для принудительного применения тригонометрических преобразований на отдельных этапах.
В сложных случаях – разбивать выражение на части и поочерёдно применять trigexpand и trigreduce.

Оптимизация выражений с переменными и параметрами через collect и combine

collect группирует слагаемые выражения по заданным переменным или параметрам, упрощая их структуру и повышая читаемость. В Maple команда имеет синтаксис collect(выражение, переменная). Она аккумулирует коэффициенты при выбранных переменных, сводя выражение к компактной форме. Это удобно при работе с многочленами и выражениями с параметрами, когда необходимо выделить основные переменные.

Например, для выражения 3*a*x + 2*b*x + 5*a*y применение collect(выражение, x) вернет (3*a + 2*b)*x + 5*a*y, что упрощает анализ зависимости от x. Если параметры заданы списком, можно группировать сразу по нескольким переменным, что полезно при сложных формулах.

combine служит для объединения степеней и преобразования выражений с экспонентами и тригонометрическими функциями. Ее основной синтаксис – combine(выражение, опции). Ключевые опции – exponentials и trig, позволяющие свести сумму или произведение степеней к более простой форме. Например, combine(exp(a)*exp(b), exponentials) преобразует в exp(a+b).

В выражениях с переменными и параметрами combine уменьшает количество операций, объединяя степени и упрощая функции, что ускоряет дальнейшие вычисления и анализ.

Рекомендации по применению:

Используйте collect для группировки по ключевым переменным до и после алгебраических преобразований, чтобы сохранить контроль над структурой выражения.
Применяйте combine к выражениям с экспонентами и тригонометрией, особенно если они содержат сложные суммы или произведения, для минимизации количества операций.
Для комплексных выражений можно последовательно вызывать collect и combine, добиваясь оптимального упрощения без потери параметрической зависимости.
В случае параметрических выражений указывайте в collect список параметров, чтобы выделить коэффициенты и избежать излишних разбиений.

Эффективное использование collect и combine в Maple обеспечивает компактные и удобные для анализа формулы, снижая вычислительную нагрузку и повышая точность при дальнейших преобразованиях.

Работа с командой eval для подстановки значений и упрощения результатов

Команда eval в Maple предназначена для подстановки конкретных значений вместо переменных в выражениях и последующего вычисления результата. Она позволяет быстро заменить символические переменные на числа, выражения или даже другие переменные.

Основной синтаксис: eval(выражение, подстановка), где подстановка – список пар «переменная = значение» или просто переменная с присвоенным значением. Например, eval(x^2 + y, {x=3, y=5}) вычислит 3^2 + 5 = 14.

Для упрощения результата после подстановки часто используют совместно с командами simplify или evalf. Пример: evalf(simplify(eval(expr, {x=2}))) – сначала подстановка, затем упрощение и численное вычисление.

Если требуется подставить несколько значений и получить список результатов, можно применять map с eval. Например, map(u -> eval(expr, u), [{x=1}, {x=2}, {x=3}]).

В случаях, когда подстановка должна учитывать параметры в уравнениях или функциях, рекомендуется использовать eval совместно с subs для точного контроля порядка подстановок и вычислений.

Следует учитывать, что eval не упрощает выражение автоматически, а лишь подставляет значения. Для получения более компактного результата необходим вызов упрощающих функций.

Использование пользовательских правил для кастомного упрощения выражений

В Maple для точечного контроля над упрощением выражений применяются пользовательские правила преобразования. Такие правила задаются в формате пар «левая часть = правая часть», где левая часть соответствует шаблону, а правая – желаемому результату преобразования.

Создание правила начинается с оператора rule := lhs = rhs. Важно использовать шаблоны с параметрами, например, a + 0 = a или sin(x)^2 + cos(x)^2 = 1. Для универсальности применяется оператор «_» – подстановочный символ, обозначающий любую подструктуру.

Для применения правил используется функция subs(rule, expr) – она заменяет все вхождения левой части на правую в выражении expr. Если требуется итеративное применение, используйте simplify(expr, transformations = {rule}) или цикл с повторным вызовом subs до отсутствия изменений.

Правила можно комбинировать, создавая списки, например: rules := {a + 0 = a, a*1 = a}. Их применение происходит через simplify(expr, transformations = rules), что значительно ускоряет кастомное упрощение сложных выражений.

Для обработки более сложных структур применяется механизм паттернов с метапеременными, например, f(_x_) = g(_x_ + 1). Это позволяет задавать универсальные шаблоны, учитывающие разные входные параметры.

Следует избегать циклических правил, вызывающих бесконечные замены. Для контроля применяется функция convert(expr, normal) перед подстановками, чтобы упрощать выражение до стандартного вида.

Пользовательские правила в Maple – мощный инструмент для точечного и эффективного управления процессом упрощения, позволяющий адаптировать преобразования под специфические задачи без потери производительности.

Вопрос-ответ:

Как выполнить упрощение сложного алгебраического выражения в Maple шаг за шагом?

Для поэтапного упрощения выражения в Maple сначала нужно ввести исходное выражение, например, с помощью команды expr := (x^2 - 1)/(x - 1);. Затем применяют функцию simplify(expr); для автоматического упрощения. Чтобы видеть промежуточные шаги, можно использовать команды, которые разбивают выражение на части, например, вручную выполнять раскрытие скобок (expand) и затем сокращение дробей. Таким образом, процесс разбивается на понятные этапы, позволяя лучше контролировать результат.

Какие команды Maple помогают раскрыть скобки и привести подобные слагаемые?

Для раскрытия скобок применяется команда expand. Например, expand((x+1)^3); преобразует выражение в сумму степеней. Для сбора и приведения подобных слагаемых используют команду collect, которая группирует члены по заданной переменной: collect(expr, x);. Эти команды часто применяют вместе для последовательного упрощения выражений.

Можно ли в Maple упростить выражение с тригонометрическими функциями и как это сделать правильно?

Да, Maple поддерживает упрощение тригонометрических выражений. Для этого применяется функция simplify с дополнительным параметром trig, то есть simplify(expr, trig);. Она приводит выражение к более удобному виду, используя тригонометрические тождества. При необходимости можно применять expand или combine для раскрытия скобок или объединения тригонометрических функций соответственно.

Как избежать ошибок при упрощении выражений с дробями в Maple?

Главная рекомендация — внимательно проверять вводимые данные и использовать правильные команды. Для упрощения дробных выражений лучше применять simplify или combine, которые приводят дроби к общему знаменателю и сокращают их. Перед этим рекомендуется раскрыть скобки с помощью expand, чтобы избежать неправильного преобразования. Если выражение содержит параметры, полезно задать им ограничения, чтобы Maple корректно обрабатывал ситуации с делением на ноль.