Как упростить выражение в wolfram mathematica

Wolfram Mathematica предоставляет широкий набор инструментов для упрощения математических выражений, которые позволяют добиться компактного и аналитически удобного вида. Ключевыми функциями являются Simplify и FullSimplify, различающиеся по глубине и времени обработки. Simplify применяет базовые преобразования, ускоряя вычисления, тогда как FullSimplify задействует более сложные методы, что полезно для сложных формул.

Для повышения эффективности упрощения важно учитывать специфику задачи: использование опций Assumptions помогает Mathematica корректно учитывать ограничения переменных, что существенно улучшает результат. Например, при работе с тригонометрическими выражениями или неравенствами введение условий позволяет избежать некорректных преобразований.

Кроме стандартных функций, Mathematica поддерживает специализированные методы, такие как TrigReduce, Factor и Collect, которые позволяют структурировать выражение под конкретные цели – разложение на множители, группировка по переменным или приведение тригонометрии к базовым формам. Комплексный подход, сочетающий эти инструменты, минимизирует время на получение оптимального результата.

Использование функции Simplify для базового упрощения выражений

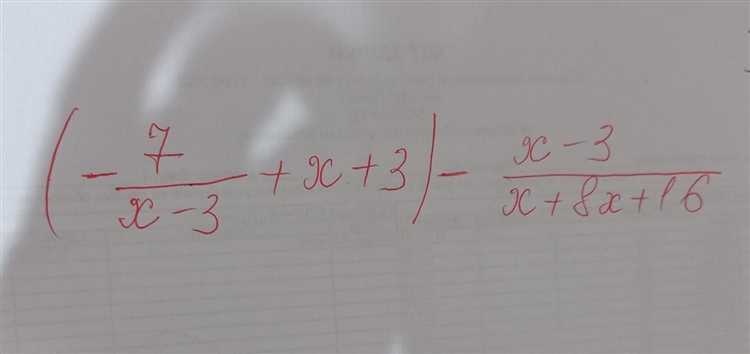
Функция Simplify выполняет преобразование математических выражений, стремясь уменьшить их сложность без изменения результата. Основной параметр, влияющий на процесс, – метрика сложности, которая учитывает количество операций, степень и количество переменных.

Для запуска базового упрощения достаточно передать выражение в Simplify[выражение]. Функция автоматически применяет правила алгебры, тригонометрии и логики, упрощая полиномы, дроби и корни.

Применение Simplify особенно эффективно при работе с выражениями, содержащими тригонометрические функции, где она преобразует выражения к более компактному виду, например, используя тождества sin²(x) + cos²(x) = 1.

Для контроля степени упрощения рекомендуется использовать опцию ComplexityFunction, позволяющую задать собственную метрику сложности. Это помогает получить результат, оптимальный именно для текущей задачи.

В ситуациях с переменными, имеющими ограничения, следует использовать второй аргумент функции, указывающий условия: Simplify[выражение, условия]. Это позволяет более точно упрощать с учетом заданных ограничений.

Функция Simplify работает быстрее, чем более мощная FullSimplify, поэтому целесообразно использовать её для первоначального упрощения, а затем при необходимости – переходить к более глубокому анализу.

Применение функции FullSimplify для глубокого преобразования формул

FullSimplify в Wolfram Mathematica предназначена для максимально полного упрощения выражений с учётом широкого спектра математических правил и эвристик. В отличие от Simplify, она задействует более обширные алгоритмы, включая распознавание тригонометрических, логарифмических, алгебраических и специальных функций, что обеспечивает глубокое преобразование формул.

Для эффективного использования FullSimplify рекомендуется задавать дополнительные условия (Constraints) через параметр Assumptions. Это существенно сокращает пространство поиска и улучшает качество результата, особенно при работе с переменными, ограниченными положительностью, целочисленностью или другими свойствами.

Оптимально применять FullSimplify к выражениям с несколькими вложенными функциями и сложными композициями, когда стандартные методы упрощения не дают результатов. При этом важно учитывать время вычисления: функция может затрачивать значительные ресурсы, поэтому рекомендуется ограничивать глубину и сложность исходного выражения либо комбинировать с Simplify для предварительной оптимизации.

Для контроля процесса преобразования доступны опции TransformationFunctions и TimeConstraint. Первая позволяет вручную расширять или сокращать набор используемых правил, вторая ограничивает максимальное время, выделяемое на упрощение, предотвращая чрезмерные вычислительные затраты.

Пример эффективного применения – упрощение выражений, содержащих корни, тригонометрические идентичности и гиперболические функции одновременно, где FullSimplify выявляет фундаментальные тождества и сокращает формулы до минимальной формы без потери точности.

Оптимизация упрощения с помощью параметров ComplexityFunction

Параметр ComplexityFunction в функциях упрощения Mathematica управляет метрикой, по которой оценивается «сложность» выражения. По умолчанию используется стандартная функция, учитывающая количество символов, операций и глубину выражения. Изменение ComplexityFunction позволяет настроить критерии выбора оптимального упрощения, ускоряя вычисления и улучшая качество результата.

Для тонкой настройки можно задать собственную функцию, которая возвращает числовую оценку, ориентированную на конкретные цели. Например, для приоритета минимизации количества операций полезно использовать LeafCount, а для сокращения длины записи – StringLength@ToString. Такой подход исключает излишнюю детализацию и фокусируется на ключевых характеристиках выражения.

Пример использования: Simplify[expr, ComplexityFunction -> LeafCount]. Это заставит Mathematica выбирать вариант с минимальным количеством узлов в дереве выражения, что часто ускоряет последующие вычисления.

Для сложных алгебраических выражений целесообразно сочетать несколько критериев в одной функции, например, взвешивая глубину выражения и число операций:

ComplexityFunction -> (LeafCount[#] + 5 Depth[#] &). Это позволяет найти баланс между компактностью и структурной простотой.

Следует учитывать, что излишне сложные ComplexityFunction могут повысить время обработки. Рекомендуется тестировать разные варианты на реальных данных для выбора оптимальной конфигурации.

Использование ComplexityFunction особенно эффективно в комбинации с функциями Simplify и FullSimplify, позволяя контролировать уровень агрессивности упрощения и избегать избыточных преобразований, не влияющих на конечный результат.

Упрощение тригонометрических выражений с помощью TrigReduce и TrigExpand

Функции TrigReduce и TrigExpand предназначены для преобразования тригонометрических выражений, каждая из которых решает специфические задачи упрощения.

TrigReduce преобразует произведения и степени тригонометрических функций в сумму или разность функций с аргументами, кратными исходному. Это удобно для интегрирования и дальнейшей аналитической обработки.
TrigExpand выполняет обратное действие – раскрывает суммы и разности аргументов внутри тригонометрических функций, приводя выражение к произведению или сумме элементарных функций.

Рекомендации по применению:

Для выражений, содержащих произведения косинусов, синусов или их степеней, используйте TrigReduce. Это упростит интегралы и преобразования.
Если выражение содержит сложные аргументы вида Sin[a + b] или Cos[a - b], применяйте TrigExpand для разложения на сумму произведений базовых функций.
Комбинируйте обе функции для пошагового упрощения: сначала TrigReduce для устранения степеней и произведений, затем TrigExpand для раскрытия сумм аргументов.
Используйте Simplify или FullSimplify после преобразований для достижения максимально компактной формы.

Пример применения:

expr = Sin[x]^2 * Cos[x];
reduced = TrigReduce[expr];
expanded = TrigExpand[reduced];

В результате TrigReduce преобразует Sin[x]^2 Cos[x] в линейную комбинацию синусов с кратными аргументами, а TrigExpand раскрывает выражение до суммы, удобной для дальнейших операций.

Работа с алгебраическими выражениями: Collect и Factor для группировки и разложения

Для структурирования алгебраических выражений в Wolfram Mathematica эффективно применять функции Collect и Factor. Обе обеспечивают разные, но взаимодополняющие способы упрощения.

Collect[выражение, переменная] группирует слагаемые по степеням указанной переменной или по нескольким переменным. Например, Collect[3 x^2 + 2 x y + y^2 + 5 x^2, x] вернёт выражение с собранными по степеням x членами: 5 x^2 + 3 x^2 + 2 x y + y^2, что позволяет легче анализировать структуру.
Опция Simplify -> True в Collect усиливает упрощение коэффициентов и внутренних частей, полезна при комбинировании с другими преобразованиями.
Коллекция может производиться по списку переменных, например, Collect[выражение, {x, y}], что упорядочивает выражение по нескольким параметрам одновременно.
Factor[выражение] осуществляет разложение многочленов на множители, выявляя скрытые факторы и упрощая анализ. Пример: Factor[x^2 - y^2] вернёт (x - y)(x + y).
Factor работает с рациональными, целочисленными и полиномиальными выражениями, позволяя эффективно выявлять общие множители и раскладывать сложные выражения.
Для глубокого разложения с учётом тригонометрических или специальных функций применяют FactorTerms или FactorList, расширяющие возможности базового Factor.

Рекомендуется:

Перед факторизацией использовать Collect для группировки по ключевым переменным, чтобы повысить наглядность выражения.
В сложных случаях с несколькими переменными проводить группировку по списку переменных для упрощения дальнейших операций.
При необходимости полного разложения применять FactorList для получения структуры множителей с их степенями.
Использовать функции последовательно: сначала Collect для структурирования, затем Factor для раскрытия множителей.

Использование Apart для разложения рациональных функций на простейшие дроби

Apart в Wolfram Mathematica позволяет эффективно разложить рациональную функцию в сумму простейших дробей. Эта операция особенно полезна при интегрировании и анализе выражений с рациональными функциями.

Синтаксис команды: Apart[выражение, переменная], где выражение – рациональная функция, а переменная – переменная, по которой выполняется разложение.

Например, для выражения (2 x^2 + 3 x + 1)/(x^3 - x) команда Apart[(2 x^2 + 3 x + 1)/(x^3 - x), x] вернет сумму дробей с линейными и квадратичными знаменателями, что облегчает дальнейшую работу с функцией.

Важно: Apart автоматически производит разложение по простым множителям знаменателя, учитывая кратность корней и корректно обрабатывая комплексные корни.

Для оптимизации работы с большими выражениями рекомендуется предварительно упростить знаменатель и числитель с помощью Simplify или Factor. Это повысит скорость и качество разложения.

Также Apart поддерживает работу с несколькими переменными, однако разложение будет выполнено только по указанной переменной, что позволяет контролировать результат и использовать функцию в многомерных задачах.

Упрощение выражений с учётом условий и предположений через Assumptions

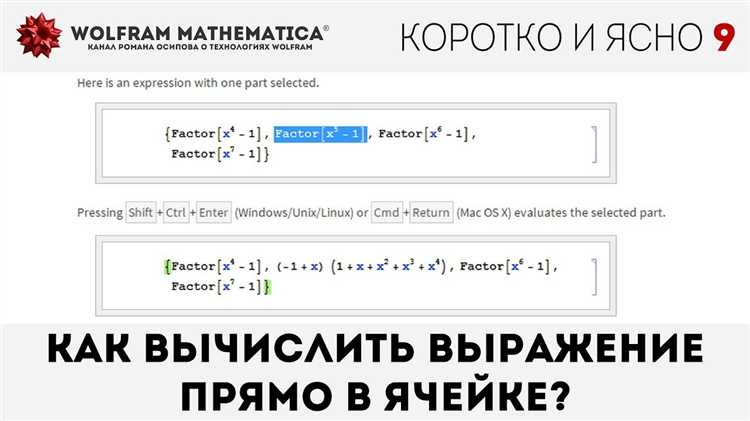
В Wolfram Mathematica для точного упрощения выражений используется параметр Assumptions, который позволяет задать конкретные условия на переменные и параметры. Это особенно важно при работе с выражениями, где результат зависит от области определения или свойств переменных.

Основной инструмент – функция Simplify или FullSimplify с опцией Assumptions. Например, выражение Sqrt[x^2] без предположений не упрощается до Abs[x], но при условии x ≥ 0 оно преобразуется в x. Запись: Simplify[Sqrt[x^2], Assumptions -> x >= 0].

Можно использовать логические связки для комбинирования предположений. Например, Assumptions -> x > 0 && y ∈ Integers позволяет учитывать сразу несколько условий, что улучшает качество упрощения сложных выражений с несколькими переменными.

Для постоянных предположений во всей сессии можно применять $Assumptions. При его корректном определении вызовы Simplify и Refine автоматически используют заданные условия, что снижает необходимость их постоянного повторного указания.

В случаях, когда нужно упростить выражения с учётом параметров, принадлежащих к определённым классам (например, действительные числа, положительные или целые), рекомендуется явно указывать это в Assumptions. Например: Assumptions -> Element[a, Reals] && a > 0.

Использование Assumptions повышает информативность и корректность результатов упрощения, устраняя амбигуитеты, вызванные отсутствием информации о параметрах. Это особенно критично при решении интегралов, пределов и дифференцировании, где свойства переменных влияют на форму ответа.

Автоматизация процесса упрощения с помощью пользовательских правил и ReplaceRepeated

В Wolfram Mathematica автоматизация упрощения выражений достигается эффективным применением пользовательских правил замены в сочетании с функцией ReplaceRepeated (//.). Правила представляют собой списки шаблонов с соответствующими преобразованиями, которые задают конкретные закономерности упрощения, недоступные стандартным функциям.

ReplaceRepeated автоматически применяет указанные правила к выражению многократно, пока оно перестает изменяться, что исключает необходимость вручную контролировать итерации. Такой подход гарантирует достижение устойчивой формы выражения с учетом всех возможных преобразований.

Для создания правил важно точно определить шаблоны, учитывающие структуру целевых выражений. Например, правило x_^2 * x_^n_ :> x_^(2 + n) объединит степени переменных, а Sin[x_]^2 + Cos[x_]^2 :> 1 заменит сумму квадратов тригонометрических функций на единицу.

Применение ReplaceRepeated с набором таких правил позволяет упростить комплексные выражения, в которых простая последовательная замена не приводит к окончательному сокращению. Рекомендуется проверять правила на специфичных подвыражениях, чтобы избежать бесконечных циклов преобразований.

Оптимально структурировать правила от наиболее специфичных к общим и группировать их в списки, которые передаются в expr //. rules. Это ускоряет сходимость процесса и обеспечивает корректность результата.

Вопрос-ответ:

Какие встроенные функции в Mathematica позволяют упростить алгебраические выражения?

Для упрощения алгебраических выражений в Mathematica часто применяются функции Simplify и FullSimplify. Simplify пытается найти более короткую или более понятную форму выражения, используя стандартные правила упрощения. FullSimplify же применяет более широкий набор трансформаций и может привести к более значительным преобразованиям, но работает дольше. Выбор между ними зависит от размера и сложности выражения, а также от требуемого результата.

Можно ли ограничить условия, при которых Mathematica упрощает выражения?

Да, обе функции — Simplify и FullSimplify — принимают необязательный параметр, который задаёт условие, при котором упрощение выполняется. Например, можно указать диапазон значений переменных или дополнительные предположения. Это позволяет получать упрощённые выражения, корректные только в заданной области или при соблюдении определённых ограничений.

Как ускорить процесс упрощения сложных выражений в Mathematica, чтобы не тратить слишком много времени?

Для ускорения стоит применять Simplify вместо FullSimplify, так как FullSimplify более ресурсоёмок. Можно также ограничить используемые правила с помощью опции ComplexityFunction, которая задаёт меру «сложности» выражения и помогает Mathematica остановить поиск, когда достигнут подходящий уровень. Кроме того, предварительное разбиение выражения на части и упрощение каждой отдельно может помочь снизить нагрузку.

Какие приёмы есть для упрощения выражений, включающих тригонометрические функции?

Для тригонометрических выражений существуют специальные функции: TrigReduce, TrigExpand и TrigSimplify. TrigReduce преобразует выражения к сумме или разности синусов и косинусов, TrigExpand раскрывает произведения и степени, а TrigSimplify пытается найти компактную форму, комбинируя эти методы. Эти инструменты дают гибкость и помогают получить более удобные формы при работе с тригонометрией.

Можно ли в Mathematica упрощать выражения с учётом заданных свойств переменных, например, что переменная — целое число или положительное число?

Да, в функциях Simplify и FullSimplify можно задать предположения о свойствах переменных с помощью опции Assumptions. Например, можно указать, что переменная целая или больше нуля, и Mathematica будет учитывать эти свойства при преобразовании. Это часто помогает получить более точные и подходящие для задачи упрощения, которые не были бы корректными без таких ограничений.

Какие основные способы упрощения выражений в Wolfram Mathematica существуют и в каких случаях их лучше применять?

Wolfram Mathematica предлагает несколько инструментов для упрощения выражений. Ключевые из них — функции Simplify и FullSimplify. Simplify выполняет базовое упрощение, используя стандартные преобразования, и быстро работает с большинством выражений. FullSimplify применяет более широкий набор правил и иногда может найти более компактный результат, но работает дольше. Для конкретных типов выражений, например, тригонометрических или алгебраических, можно использовать специализированные функции вроде TrigReduce или Factor. Выбор зависит от задачи: если нужна быстрая проверка или небольшая оптимизация — Simplify, если важна максимальная компактность или глубокое преобразование — FullSimplify. Дополнительно полезно задавать ограничения (условия) для упрощения, чтобы Mathematica учитывала особенности переменных.

Как ограничить область упрощения в Mathematica, чтобы избежать потери важных свойств выражения?

Иногда полное упрощение приводит к изменению области определения или к тому, что выражение теряет свойства, важные для задачи. В таких случаях можно использовать опции функций упрощения, например, задавать условие с помощью параметра Assumptions. Это позволяет указать, над какими переменными и при каких ограничениях проводится упрощение — например, что переменные вещественные или положительные. Такой подход помогает избежать нежелательных преобразований, которые могли бы изменить смысл выражения. Кроме того, есть функция Refine, которая упрощает выражение с учетом заданных предположений, не меняя его структуру слишком сильно. Это позволяет контролировать процесс и получать результат, который точно соответствует требованиям задачи.