В Mathcad функция root используется для нахождения корня уравнения или системы уравнений. Эта функция позволяет быстро решать задачи, связанные с вычислением значений, при которых выражение или уравнение равно нулю. Однако, как и большинство функций Mathcad, root имеет необязательные аргументы, которые могут быть опущены, если это не требуется для конкретной задачи.
Основной аргумент функции root – это выражение, корень которого нужно найти. Это обязательный аргумент. Но кроме этого, есть несколько необязательных параметров, которые можно использовать для уточнения решения или управления процессом вычислений. Например, аргумент начальное приближение (начальное значение переменной) помогает функции быстрее найти решение при сложных уравнениях или в случае, если решение не уникально. Если этот аргумент не указан, Mathcad автоматически выберет приближение.
Другим необязательным аргументом является максимальное количество итераций, которое указывает, сколько раз функция будет пытаться приблизиться к корню. Это важно для сложных вычислений, где требуется высокая точность, а без ограничения итераций функция может работать слишком долго. В случае, если это значение не задано, Mathcad использует стандартное количество итераций.
Наконец, также можно задать порог погрешности, который определяет, насколько точным должно быть решение. Если порог не задан, Mathcad будет использовать стандартное значение. Указание более строгих условий может ускорить решение задачи, но также потребует больше вычислительных ресурсов.
Как правильно использовать необязательные аргументы функции root
Функция root в Mathcad используется для нахождения корней уравнений, и она принимает два обязательных аргумента: функцию и диапазон значений. Однако, кроме этих обязательных, существуют необязательные аргументы, которые могут улучшить точность или ускорить вычисления. Правильное использование этих аргументов существенно повышает эффективность работы с функцией root.
Необязательные аргументы функции root в Mathcad следующие:
- Начальное приближение (Initial Guess) – это значение, с которого начинается поиск корня. Если аргумент не задан, Mathcad будет использовать стандартное приближение, что может привести к медленным или даже ошибочным вычислениям. Правильный выбор начального приближения важен для ускорения нахождения корня и повышения его точности.
- Метод вычисления (Method) – этот аргумент позволяет выбрать метод поиска корня, например, метод Ньютона или метод бисекции. Если метод не задан, Mathcad автоматически применяет метод Ньютона, который работает быстрее, но может быть неэффективным при сложных или многозначных уравнениях. Для сложных функций с несколькими корнями или особенностями стоит выбрать метод бисекции.
- Точность (Tolerance) – аргумент, определяющий точность нахождения корня. Если не указана точность, Mathcad использует значение по умолчанию. Указание собственной точности позволяет более точно настроить результат в зависимости от требований задачи.
- Максимальное количество итераций (Max Iterations) – этот аргумент ограничивает число итераций, которые будет выполнять алгоритм. Если максимальное количество итераций не задано, Mathcad использует стандартное значение, что может повлиять на скорость вычислений. Установите лимит итераций, если задача требует быстрого, но не обязательно точного результата.
Рекомендуется всегда учитывать особенности решаемой задачи при выборе значений для этих аргументов. Например, если корень уравнения лежит в определенном диапазоне и известно приближенное значение, задайте начальное приближение вблизи этого значения, чтобы ускорить процесс поиска. Для уравнений с несколькими корнями, установка метода на «бисекция» или использование более точных значений для «Точности» уменьшает вероятность ошибок.
Кроме того, при использовании метода «Ньютон» важно учитывать возможные особенности функции, такие как локальные экстремумы или разрывы, которые могут повлиять на сходимость метода. В таких случаях установка метода на «бисекция» или выбор другого стартового приближения поможет избежать застревания алгоритма.
Таким образом, оптимальное использование необязательных аргументов функции root требует внимательности к спецификации задачи, учета точности вычислений и выбора наиболее подходящего метода для нахождения корней. Это позволяет значительно повысить скорость и точность решения уравнений в Mathcad.
Что происходит, если не указать начальное приближение в root
Если не указать начальное приближение в функции root в Mathcad, система автоматически применит стандартное значение для этого аргумента. В большинстве случаев Mathcad использует значение, которое обеспечит сходимость алгоритма к одному из корней уравнения. Однако результаты могут зависеть от характеристик функции, с которой работает алгоритм.
Варианты поведения системы без начального приближения:
- Использование «нулевого» приближения: Если начальное приближение не задано, Mathcad может попытаться начать с нулевого значения. Это может привести к неправильному результату, если функция имеет особенности вблизи нуля (например, асимптоты или экстремумы).
- Алгоритм может не сойтись: В случае сложных функций, с несколькими корнями или особенностями, отсутствие начального приближения может привести к тому, что алгоритм не найдет решение. Алгоритм может либо зациклиться, либо вернуться с ошибкой сходимости.
- Случайный выбор начального приближения: В некоторых случаях Mathcad может выбрать случайное значение, что увеличивает вероятность нахождения локального, а не глобального корня. Это может быть полезно, если функция имеет несколько корней, однако точность решения будет зависеть от конкретной задачи.
Рекомендуется всегда задавать начальное приближение, чтобы минимизировать риски ошибок сходимости или получения некорректных результатов. Особенно это важно для функций, которые имеют несколько решений, или для тех, что демонстрируют резкие изменения в значениях.
Какие параметры можно пропустить при решении уравнений с несколькими корнями
При решении уравнений с несколькими корнями в Mathcad функция root предоставляет несколько аргументов, из которых некоторые можно опустить в зависимости от контекста задачи. Важно понимать, какие из них обязательны, а какие могут быть пропущены, чтобы упростить решение.
Основные аргументы функции root включают выражение, начальное приближение и параметры, задающие диапазон поиска корней. Однако не все из них обязательны:
- Начальное приближение – этот параметр помогает функции найти ближайший корень уравнения. Если его не указать, Mathcad будет использовать значения по умолчанию, что может привести к нахождению неверного или несуществующего корня, особенно если уравнение имеет несколько решений. Пропуск этого параметра допустим, но требует внимательности к контексту задачи.
- Диапазон поиска – этот параметр ограничивает область, в которой будет производиться поиск корня. Если его не указать, Mathcad будет использовать весь возможный диапазон. Однако, если у вас есть конкретное предположение о месте нахождения корня, его указание ускоряет решение и снижает вероятность ошибки. Этот параметр можно пропустить, если важно найти корень в целом диапазоне.
- Точность решения – в большинстве случаев Mathcad будет использовать стандартную точность, которая подходит для большинства задач. В случае, если требуется высокая точность, можно задать этот параметр вручную. Пропуск этого параметра допустим, но результат может не удовлетворять точностным требованиям.
Таким образом, параметры, которые можно пропустить при решении уравнений с несколькими корнями в Mathcad, зависят от конкретной задачи. Однако всегда важно понимать, что отсутствие начального приближения или диапазона поиска может повлиять на точность и корректность решения.
Влияние опущенных значений на точность вычислений

При опущении аргумента точности вычислений Mathcad использует значение по умолчанию, которое может быть недостаточным для решения некоторых сложных задач. В таких случаях результаты могут отличаться от истинных значений из-за округлений или использования приближенных методов решения. Для минимизации погрешностей рекомендуется всегда явно указывать значение точности, особенно если решение зависит от малого изменения параметров.
Неопределенность значений также возникает при отсутствии начального приближения. Без указанного начального значения корня Mathcad выбирает его по умолчанию, что может привести к неправильному результату при наличии нескольких корней у уравнения. Для повышения точности вычислений в таких случаях лучше явно задавать начальное приближение, подходящее для данной задачи.
Опускать значения в функции root можно только в тех случаях, когда их влияние на результат минимально или известно заранее. В остальных ситуациях важно тщательно проверять все параметры, чтобы избежать ошибок в решении. Рекомендуется проводить тестирование и сверку результатов для подтверждения их точности.
Как задавать границы для поиска корня без обязательных параметров
В Mathcad для поиска корня функции с помощью оператора root обычно требуется указать два обязательных параметра: сама функция и начальное приближение. Однако для более точной настройки можно задать дополнительные параметры, такие как границы для поиска корня. Это позволяет повысить точность результата и ускорить вычисления. Важно понимать, как это сделать, чтобы не столкнуться с ошибками и неэффективностью в расчетах.
По умолчанию функция root использует глобальные границы поиска, если они не заданы вручную. Однако в некоторых случаях имеет смысл указать конкретный диапазон, в котором функция имеет корень. Это особенно важно для сложных функций с несколькими корнями или при наличии экстремумов, которые могут привести к неправильному результату без должной настройки границ.
Как задать границы: Для этого необходимо использовать необязательные параметры lower и upper, которые указывают на минимальное и максимальное значение, в пределах которых будет осуществляться поиск. Важно, чтобы значения lower и upper действительно ограничивали область, в которой лежит корень, иначе функция не сможет корректно вычислить решение.
Пример: Для нахождения корня функции f(x) = x^2 - 4 в интервале от 1 до 3, можно записать следующее:
root(f(x), 1, 3)
Это гарантирует, что функция будет искать корень только в пределах заданного интервала. При этом если значение корня не лежит в указанной области, функция выдаст ошибку или сообщение о невозможности нахождения решения.
Рекомендации:
- Задавайте границы исходя из особенностей функции. Например, для монотонных функций поиск корня в одном интервале будет более эффективным.
- Используйте границы для функций с несколькими корнями, чтобы точно указать область поиска и избежать нахождения ненужных корней.
- Если не уверены в значении корня, начните с более широких границ, постепенно сужая диапазон.
Таким образом, знание о настройке границ поиска для функции root в Mathcad позволяет значительно улучшить точность и эффективность вычислений, а также избежать возможных ошибок в расчетах.
Как Mathcad обрабатывает отсутствие максимального числа итераций в root
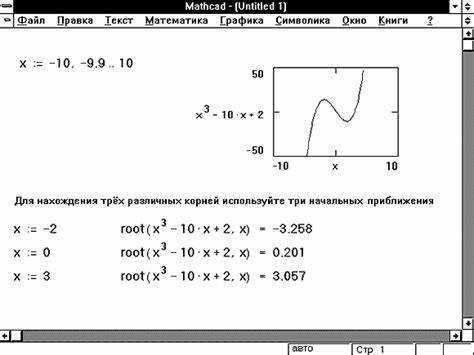
В Mathcad, когда аргумент максимального числа итераций в функции root не задан, программа использует значение по умолчанию для этого параметра. Это значение составляет 50. Если за это количество итераций решение не найдено, Mathcad завершает вычисления и выдает сообщение об ошибке, указывающее на невозможность нахождения корня при заданных условиях.
Отсутствие явного указания максимального числа итераций дает пользователю возможность избежать лишнего контроля за этим параметром, если предполагается, что поиск корня не займет слишком много времени. Однако важно понимать, что при слишком большом значении итераций, особенно в сложных или плохо обусловленных задачах, можно столкнуться с чрезмерными вычислительными затратами, что снижает производительность программы.
Чтобы улучшить работу с этой функцией, рекомендуется использовать максимальное количество итераций с учетом специфики задачи. В случаях, когда корень может быть найден за меньшее количество шагов, можно вручную задать число итераций, чтобы ускорить процесс и предотвратить затраты времени на излишние вычисления.
Важно также учитывать, что если значение максимального числа итераций слишком велико, это не всегда будет гарантиром корректного решения. Множество итераций без нужды может привести к неоптимальным результатам, особенно в случае нелинейных уравнений или проблем с плохой сходимостью. В таких случаях полезно дополнительно контролировать параметры погрешности и допусков, чтобы получить более точные результаты при разумных затратах времени.
Примеры ситуаций, когда можно не указывать шаг сходимости

1. Простой случай с явно сходящимися уравнениями
Если уравнение имеет один корень, расположенный далеко от других возможных решений, и вы уверены в его единственности, можно не задавать шаг сходимости. Mathcad самостоятельно подберет оптимальный шаг, особенно если уравнение не содержит сложных и неопределенных выражений, таких как дроби с переменными в знаменателе.
2. Точное математическое моделирование
При моделировании в системах, где уравнение представлено точной аналитической формулой (например, полиномиальные уравнения второй или третьей степени), шаг сходимости можно опустить. В таких случаях Mathcad способен быстро найти корень, поскольку алгоритм точно понимает структуру уравнения и не требуется дополнительных уточнений по сходимости.
3. Положительные или отрицательные решения, предсказуемые заранее
Если известно, что решение находится в пределах определенного диапазона значений (например, корень всегда положителен или отрицателен), функция будет использовать этот диапазон для уточнения ответа. В таком случае шаг сходимости не будет влиять на результат, так как алгоритм уже ограничен нужным интервалом.
4. Уравнения с явными ограничениями
Если уравнение имеет ограничения (например, переменная x не может принимать значения, выходящие за пределы определенного диапазона), Mathcad сам выбирает шаг сходимости, учитывая эти ограничения. При этом гарантируется, что решение не выйдет за пределы допустимых значений, и шаг будет подобран автоматически.
5. Простые численные методы
Когда для нахождения корня используется метод, который по своей природе быстро сходится (например, метод Ньютона для функции с гладкими и непрерывными производными), можно не задавать шаг сходимости. В таких случаях Mathcad автоматически подбирает оптимальные параметры, так как они практически не влияют на точность вычислений.
Когда игнорировать функцию для вычисления производной в root
В Mathcad функция root используется для нахождения корней уравнений, а также для вычисления производных в контексте решений. Однако в некоторых случаях разумно игнорировать производную при использовании этой функции. Это может снизить вычислительные затраты и повысить стабильность решения.
Если задача требует нахождения корней уравнения, и функция производной не используется для улучшения сходимости алгоритма, можно обойтись без неё. Например, если у вас есть хорошо заданная монотонная функция, изменение которой не вызывает резких колебаний или точек перегиба, использование производной может быть избыточным. В таких случаях поиск корня может быть выполнен без дополнительных вычислений, связанных с нахождением производной.
Когда функция не имеет экстремумов в области решения, производная в контексте поиска корней также не приносит пользы. Если уравнение имеет четко определённые интервалы решения и график функции не ведет к неопределённым точкам или многозначности, отключение вычисления производной может ускорить процесс нахождения корня.
Определение точности решения также влияет на необходимость вычисления производной. В некоторых задачах, где достаточно приближённого решения, отключение производной может существенно снизить вычислительные ресурсы, не снижая точности. Например, в ситуациях, когда требуется нахождение корня с точностью до нескольких знаков после запятой, дополнительные вычисления, связанные с производной, могут быть избыточными.
Если же задача состоит в нахождении решения сложной функции с несколькими переменными, то использование производной не стоит игнорировать, так как это может помочь улучшить сходимость метода Ньютона или других численных алгоритмов. Но в контексте простых однородных функций, особенно тех, где изменение знака достаточно очевидно, производная не требуется.
Таким образом, игнорировать производную в root стоит в случаях, когда её вычисление не даёт значительного улучшения сходимости или точности решения, и можно ограничиться более быстрым методом поиска корней, без потери качества вычислений.
Вопрос-ответ:
Какие аргументы функции root являются необязательными в Mathcad?
В Mathcad функция root используется для нахождения корней уравнений. Эта функция имеет несколько аргументов, однако не все из них являются обязательными. Главный обязательный аргумент — это уравнение, для которого необходимо найти корень. Дополнительные необязательные аргументы включают начальное приближение и пределы решения. Начальное приближение помогает алгоритму быстрее найти решение, но его можно не указывать, если система самостоятельно сможет найти корень. Если начальное приближение не задано, функция будет искать решение в пределах возможных значений.
Что происходит, если не указать начальное приближение для функции root в Mathcad?
Если не указать начальное приближение для функции root в Mathcad, то программа попытается найти корень уравнения без предварительного указания точки, с которой начинать поиск. Это может привести к более длительному вычислительному процессу, особенно если у уравнения несколько корней или оно имеет сложную форму. Однако Mathcad имеет алгоритмы, которые помогают находить решения даже без начального приближения, хотя скорость нахождения корня может быть ниже.
Можно ли использовать функцию root без указания предела решения в Mathcad?
Да, в Mathcad функция root может работать и без указания предела решения. Предел решения задает допустимую точность для нахождения корня, но это необязательный аргумент. Если предел не указан, Mathcad будет использовать стандартную точность, которая может быть достаточной для большинства задач. Тем не менее, если требуется более высокая точность, лучше указать предел, чтобы убедиться, что решение будет найдено с нужной точностью.
Какие факторы влияют на необходимость указания необязательных аргументов функции root в Mathcad?
Необязательные аргументы функции root в Mathcad, такие как начальное приближение и предел решения, зависят от сложности уравнения. Например, если у уравнения есть только один корень, указание начального приближения не всегда обязательно. Однако если уравнение имеет несколько корней или сложную структуру, начальное приближение может значительно ускорить процесс вычислений. Предел решения становится важным, если требуется высокая точность, особенно при работе с уравнениями, которые могут иметь чувствительность к малым изменениям параметров.
Как выбрать начальное приближение для функции root в Mathcad?
Выбор начального приближения для функции root в Mathcad зависит от формы уравнения и ожидаемого значения корня. Хорошим вариантом будет использовать график функции для визуальной оценки местоположения корня, что поможет выбрать более точное начальное приближение. Если график недоступен, можно начать с произвольного значения и постепенно уточнять его. В некоторых случаях, если корней несколько, потребуется провести несколько вычислений с разными начальными приближениями для нахождения всех решений.
Какие аргументы функции root являются необязательными в Mathcad?
В Mathcad функция root используется для нахождения корня уравнения, и она принимает несколько аргументов. Однако, не все из них обязательны. Главным обязательным аргументом является сам уравнение, корень которого нужно найти. Дополнительные аргументы, такие как начальное приближение, максимальное количество итераций или точность вычислений, являются необязательными. Если эти параметры не указаны, Mathcad будет использовать значения по умолчанию, что позволяет упростить использование функции.
Почему некоторые аргументы функции root в Mathcad необязательны?
В Mathcad некоторые аргументы функции root являются необязательными для того, чтобы упростить процесс вычислений и сделать его более гибким. Например, если не указано начальное приближение, программа автоматически использует стандартное значение. Это позволяет пользователю сосредоточиться на самой задаче без необходимости детально настраивать параметры функции, особенно в случаях, когда точность и количество итераций не критичны для решения. Вдобавок, такие параметры могут быть использованы только в случае, если требуется дополнительная настройка вычислений для более сложных задач.