Какие бывают векторы в mathcad

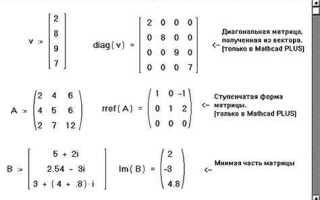
В среде Mathcad векторы представляют собой одномерные массивы, состоящие из чисел или выражений, индексируемых с определённой позиции. По умолчанию индексация начинается с 0, но это значение можно изменить в настройках, что критично при работе с математическими моделями, чувствительными к нумерации элементов.

Существует два ключевых типа векторов в Mathcad: строчные векторы и столбцовые векторы. Строчные векторы создаются через ввод элементов в строку с разделением запятыми, тогда как столбцовые – с использованием клавиши Enter между элементами. От выбора типа зависит корректность операций умножения и транспонирования, поскольку Mathcad строго различает размерности.

При выполнении линейных алгебраических операций, таких как скалярное произведение или умножение матрицы на вектор, необходимо строго соблюдать соответствие размеров: столбцовый вектор можно умножить на матрицу только при согласовании размерностей. Mathcad не выполняет автоматическое приведение типов векторов, поэтому необходимо вручную использовать функцию transpose() или клавишу Ctrl+T для транспонирования.

В задачах численного моделирования часто применяются программно сгенерированные векторы с использованием функции range, например, x := 0, 0.1 .. 10. Такой вектор удобно использовать для построения графиков, численного интегрирования или подстановки в системы уравнений. Mathcad позволяет использовать эти векторы напрямую в функциях без необходимости разворачивать цикл.

Эффективное использование векторов в Mathcad требует чёткого понимания их структуры и поведения при арифметических и логических операциях. При этом важным преимуществом среды является визуальная наглядность операций и контроль над индексами, что особенно полезно при работе с инженерными расчётами и прикладными задачами.

Создание строковых и столбцовых векторов в рабочем листе

В Mathcad строковые и столбцовые векторы отличаются направлением индексации и способом ввода. Столбцовый вектор создаётся автоматически при поэлементном вводе значений с нажатием клавиши Enter после каждого элемента. Например, при вводе v := и последовательном нажатии Enter после каждого значения (например, 3 Enter 5 Enter 7), Mathcad создаёт вектор-столбец размерностью 3×1.

Чтобы создать строковый вектор, используйте оператор транспонирования. Сначала создайте вектор-столбец, затем примените операцию транспонирования с помощью символа апострофа ('). Пример: v' → строковый вектор. Размерность изменится на 1×n. Строковый вектор можно также получить через программное задание, например: v := [3, 5, 7], с последующим указанием индексов вручную.

При необходимости создать вектор с конкретной размерностью и направлениями удобно использовать функцию vector(n), а затем присвоить каждому элементу нужное значение через индексную нотацию v[i := значение. Учитывайте, что в Mathcad индексация начинается с нуля, если явно не задано иное через переменную ORIGIN.

При вычислениях важно понимать, что операции умножения, деления и транспонирования чувствительны к ориентации вектора. Например, произведение строкового вектора на столбцовый (1×n)×(n×1) даёт скаляр, а обратный порядок (n×1)×(1×n) формирует матрицу размером n×n.

Различия в обработке одномерных массивов и векторов

В Mathcad вектор и одномерный массив – не идентичные структуры. Вектор имеет чётко определённое направление (строка или столбец) и индекс, начинающийся с нуля или заданный пользователем. Одномерный массив, в отличие от вектора, может трактоваться как частный случай двумерной матрицы с одной строкой или одним столбцом, но без гарантий направления при выполнении операций.

При транспонировании поведение различается: вектор-столбец становится вектором-строкой, а одномерный массив может быть неявно интерпретирован как строка, что вызывает ошибки в операциях умножения и сложения с матрицами. В Mathcad выражения вида A∙B работают корректно только при согласованности направлений, особенно если один из операндов – вектор, а другой – одномерный массив. Ошибки типа «несовместимые размеры» часто возникают при смешении этих структур.

Функции, такие как mean(), sort() и max(), применённые к вектору, обрабатывают его поэлементно, учитывая направление. К одномерному массиву – с учётом его представления в памяти, что может привести к неожиданным результатам. Например, mean(v) для вектора корректно возвращает среднее значение, но тот же вызов для одномерного массива, интерпретируемого как строка, может вызвать сбой при последующей обработке.

Для надёжной работы с данными рекомендуется явно преобразовывать одномерные массивы в векторы с помощью функций transpose() или augment(), задавая требуемое направление. Это критично при автоматизации вычислений или передаче данных между функциями и скриптами внутри Mathcad.

Использование встроенных функций для работы с векторами

Mathcad предоставляет широкий набор встроенных функций для эффективной работы с векторами. Эти функции позволяют выполнять арифметические операции, анализировать данные, производить преобразования и получать статистические характеристики без необходимости ручного программирования.

• sum(v): возвращает сумму всех элементов вектора v. Используется для расчёта общего значения, например, при анализе временных рядов.
• mean(v): вычисляет среднее значение элементов. Полезна при предварительной обработке данных.
• max(v), min(v): определяют максимальное и минимальное значения. Часто применяются при поиске экстремумов в числовых рядах.
• sort(v): сортирует вектор по возрастанию. Используется перед применением функций ранжирования или медианы.
• rank(v): возвращает вектор рангов исходных значений. Полезен в статистике для сравнения распределений.
• cumsum(v): создаёт вектор накопленных сумм, что удобно при анализе трендов и интеграции по дискретным данным.
• diff(v): возвращает вектор разностей между соседними элементами. Применяется для анализа скорости изменения данных.
• submatrix(v, i, j): извлекает подмножество элементов, позволяя манипулировать частями вектора.

При создании пользовательских вычислений рекомендуется комбинировать эти функции. Например, для нормализации вектора v можно использовать выражение: (v - mean(v)) / stddev(v), где stddev(v) – стандартное отклонение.

Для векторов большой размерности целесообразно применять векторизованные операции вместо циклов: Mathcad автоматически обрабатывает векторные аргументы, что ускоряет выполнение вычислений.

Использование встроенных функций делает код компактным, понятным и легко масштабируемым при работе с массивами данных различной структуры.

Инициализация векторов с помощью программных блоков

Программный блок в Mathcad позволяет создавать векторы с гибкой логикой и параметризацией. Он оформляется через конструкции if, for, while и операторы присваивания. Инициализация вектора начинается с задания его длины и создания переменной-вектора через оператор :=.

Для заполнения вектора в цикле for используется счётчик, задаваемый через ключевое слово for i ∈ range. Пример: for i ∈ 0..N-1 создает индексированный доступ к элементам вектора от 0 до N–1. Внутри цикла каждому элементу присваивается значение: v[i := выражение]. Все индексы в Mathcad по умолчанию начинаются с нуля, если не изменено в Calculation Options → Built-in Variables.

Программный блок может использовать вложенные циклы и условные операторы для создания векторов с зависимой структурой. Например, генерация вектора Фибоначчи: первый и второй элементы задаются явно, а остальные – как сумма двух предыдущих. Это невозможно реализовать через стандартное выражение без блока.

Инициализация с помощью программного блока особенно полезна для нестандартных правил генерации элементов, пошаговой фильтрации, адаптивной дискретизации. После завершения блока, выходная переменная автоматически отображает сгенерированный вектор в рабочей области. Mathcad корректно интерпретирует размерность и позволяет использовать его в дальнейших расчетах без дополнительных преобразований.

Построение графиков на основе векторных данных

В Mathcad построение графиков осуществляется напрямую из векторных переменных, без необходимости предварительного преобразования данных. Для отображения зависимости одного параметра от другого используются двухвекторные графики: ось X формируется из одного вектора, ось Y – из другого той же длины.

Пример: заданы векторы x := 0, 0.1 .. 10 и y := sin(x). Построение графика выполняется вставкой графического элемента (2D Plot) и вводом имён переменных в соответствующие поля. Mathcad автоматически сопоставляет точки по индексам векторов.

Векторные данные допускают построение нескольких кривых на одном графике. Если определить y1 := sin(x), y2 := cos(x), то в поле Y можно ввести y1, y2 – результатом будет наложение синуса и косинуса на общий X-интервал.

Для трехмерных графиков используются матрицы или вложенные векторы. Пример: z(i,j) := sin(x(i))·cos(y(j)), где x и y – независимые векторы. График строится с использованием элемента Surface Plot, в поля вводятся переменные x, y и z.

Для получения точных графиков важно следить за равномерностью шага дискретизации и корректной длиной векторов. Ошибка в размере хотя бы одного из них приводит к некорректному отображению или сбою построения.

Изменение параметров графика (цвет, масштаб, оси) производится через контекстное меню графика. Векторные подписи и обозначения добавляются с помощью текстовых элементов и ссылок на переменные.

Обращение к элементам вектора и изменение значений

В Mathcad обращение к элементам вектора осуществляется через индекс, указываемый в квадратных скобках. Нумерация элементов начинается с 0. Для доступа к конкретному элементу записи вида:

V[i]

где V – вектор, i – индекс элемента.

• Индекс i должен быть целым числом в диапазоне от 0 до длины вектора минус 1.
• При выходе за границы индексации Mathcad выдаст ошибку.

Для изменения значения элемента вектора достаточно присвоить новое значение по индексу:

V[i := новое_значение]

Пример:

V[2 := 7

изменит третий элемент вектора V на 7.

Mathcad поддерживает также диапазон индексов для одновременного обращения к нескольким элементам:

V[1..3]

возвращает подмассив с элементами с индексами 1, 2 и 3. Для изменения нескольких элементов можно использовать оператор присваивания с диапазоном:

V[1..3 := [5, 6, 7]]

где справа указывается вектор новых значений. Длина правой части должна совпадать с числом элементов в диапазоне.

• Обращение к элементам возможно как для строковых, так и для столбцовых векторов.
• Для элементов, зависящих от параметров, допускается использовать переменные индексы, вычисляемые в формуле.

Практические рекомендации:

1. Всегда проверяйте длину вектора перед изменением значений, чтобы избежать ошибок индексации.
2. Для замены нескольких подряд идущих значений используйте диапазон индексов и вектор новых значений.
3. Избегайте использования отрицательных индексов, они не поддерживаются в Mathcad.
4. При необходимости выделения отдельных элементов используйте отдельные обращения V[i] вместо создания промежуточных копий векторов.

Применение векторов в численных расчетах и моделировании

В численных расчетах и моделировании векторы служат базовым инструментом для представления и обработки данных, характеризующих пространственные величины и многомерные параметры систем. В Mathcad векторы позволяют эффективно задавать начальные условия, параметры и результаты расчетов в компактном и управляемом виде.

Для анализа механических систем векторы используются для описания сил, скоростей и перемещений, что позволяет применять методы линейной алгебры для решения уравнений движения. В физическом моделировании векторы формируют поля интенсивностей (например, электрических или магнитных), обеспечивая удобство вычисления градиентов и дивергенций.

В численных методах оптимизации векторы параметров систем упрощают применение градиентных и нулевых методов поиска экстремумов, поскольку позволяют легко организовать вычисления производных и обновление переменных. В задачах интерполяции и аппроксимации многомерных функций векторы значений функции и аргументов упрощают формирование систем уравнений для построения полиномов или сплайнов.

В Mathcad рекомендуется использовать векторы фиксированной длины для оптимизации вычислительных ресурсов, особенно при многократных итерациях. Для динамического моделирования целесообразно применять векторы с функциями, что позволяет отслеживать изменения во времени без дополнительного программирования.

Работа с векторами в Mathcad должна сопровождаться контролем размерности, поскольку несоответствие размеров векторов приводит к ошибкам вычислений. Практика показывает, что применение встроенных функций векторизации повышает точность и снижает время выполнения сложных моделей за счет минимизации циклических операций.

Связь векторов с матрицами и правила преобразования

В Mathcad векторы рассматриваются как частный случай матриц с одной строкой (строчные векторы) или одним столбцом (столбцовые векторы). Такое представление позволяет применять операции с матрицами напрямую к векторам, что упрощает вычисления и трансформации.

Преобразования векторов посредством матриц реализуются через умножение матрицы на вектор. При этом размерность матрицы должна соответствовать размерности вектора: для столбцового вектора A размером n×1 матрица преобразования должна быть n×n или m×n, где m – размерность результирующего вектора.

В Mathcad важно корректно задавать тип вектора перед преобразованием. Например, для поворотов и масштабирования в пространстве применяется матрица 3×3, а для аффинных преобразований – расширенная матрица 4×4 с использованием однородных координат. Это обеспечивает точность и однозначность результата.

Правила преобразования требуют соблюдения порядка операций: умножение матрицы на вектор следует выполнять слева направо, учитывая, что вектор – столбцовый. Если вектор представлен как строка, необходимо преобразовать его в столбец для правильного умножения.

При работе с векторными функциями в Mathcad рекомендуется использовать встроенные операции матричного умножения (например, оператор «*»), избегая поэлементных функций, чтобы не допустить ошибок в размерностях и ускорить вычисления.

Векторы, преобразованные с помощью матриц, сохраняют линейные свойства, что критично при решении задач линейной алгебры и геометрических преобразований. Для проверки корректности преобразования можно сравнить нормы исходного и итогового векторов, если преобразование сохраняет длину, или проанализировать компоненты после преобразования.

Вопрос-ответ:

Какие виды векторов поддерживает Mathcad и в чем их отличия?

Mathcad позволяет работать с различными типами векторов: строковыми, столбцовыми и произвольными одномерными массивами. Строковый вектор представлен как горизонтальная последовательность элементов, а столбцовый — как вертикальная. Эти различия важны для выполнения операций, таких как умножение матриц или применение функций, зависящих от ориентации данных. Кроме того, в Mathcad можно задавать векторы с различным типом элементов — числовые, логические или символические.

Как можно использовать векторы в Mathcad для решения систем линейных уравнений?

Для решения систем линейных уравнений в Mathcad часто применяют векторы, представляющие неизвестные переменные и свободные члены. Коэффициенты системы формируют матрицу, а вектор свободных членов — отдельный столбец. С помощью встроенных функций можно найти вектор решения, используя операцию умножения обратной матрицы на вектор свободных членов. Такой подход упрощает обработку больших систем и позволяет быстро получать численные значения переменных.

Можно ли в Mathcad выполнять операции сложения и умножения с векторами разной длины?

Операции сложения и умножения в Mathcad требуют, чтобы длины векторов совпадали, иначе программа выдаст ошибку. Если векторы разной длины, нужно привести их к одинаковому размеру, например, добавив нулевые элементы. Для умножения на скаляр длина не имеет значения, так как скаляр умножается на каждый элемент вектора по отдельности.

Как преобразовать строковый вектор в столбцовый в Mathcad и зачем это может понадобиться?

В Mathcad для преобразования строкового вектора в столбцовый используется функция транспонирования, обозначаемая обычно апострофом (‘). Такое преобразование важно, когда требуется согласовать размерности векторов для операций умножения или для работы с матрицами. Например, если имеется строковый вектор и нужно умножить его на столбцовый, один из них нужно транспонировать, чтобы получить корректный результат.

Какие примеры применения векторов в инженерных расчетах с Mathcad вы можете привести?

Векторы широко применяются в инженерных расчетах для представления сил, скоростей, перемещений и других величин, имеющих направление и величину. В Mathcad их используют для анализа напряжений в конструкциях, расчета динамических систем, обработки экспериментальных данных. Например, в задаче механики можно задать векторы сил, а затем вычислить результирующую силу через сумму векторов, что упрощает визуализацию и расчет параметров системы.

Какие виды векторов поддерживаются в Mathcad и чем они отличаются?

В Mathcad используются векторы строковые, столбцовые и одномерные массивы. Строковые векторы представлены в виде горизонтальных последовательностей элементов, а столбцовые — вертикальных. Это различие важно для выполнения операций, таких как умножение матриц, где ориентация влияет на результат. Кроме того, Mathcad позволяет создавать векторы с элементами разных типов данных, но для большинства вычислений лучше использовать числовые векторы. Понимание формата векторов помогает корректно организовать данные и избежать ошибок при расчетах.

Как применять векторы в Mathcad для решения задач линейной алгебры?

Векторы в Mathcad широко используются для операций линейной алгебры, включая сложение, умножение на скаляр, вычисление скалярного и векторного произведений. Например, при решении систем уравнений вектор может выступать как столбец неизвестных, а матрица — как коэффициенты. Mathcad автоматически поддерживает необходимые операции с векторами, упрощая вычисления и позволяя быстро получить решения. Кроме того, векторы применимы при построении графиков и анализе данных, что расширяет возможности работы с числовой информацией.