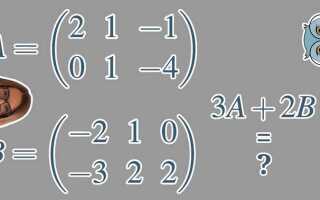Какие действия с матрицами можем выполнять в mathcad

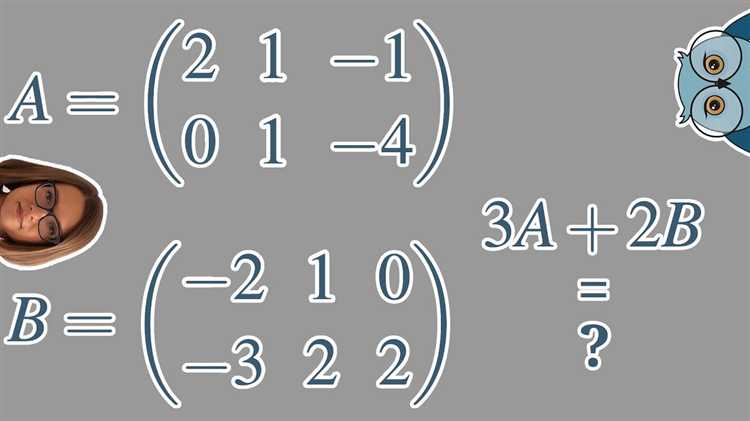
Mathcad предоставляет мощный инструментарий для работы с матрицами, позволяя выполнять сложные вычисления в инженерных и научных задачах. В отличие от традиционных языков программирования, ввод и редактирование матриц в Mathcad реализованы через визуальное представление, что минимизирует количество синтаксических ошибок и упрощает восприятие структуры данных.

Создание матрицы осуществляется через прямой ввод элементов с указанием индексов или с использованием функции matrix, где задаются размеры и содержимое. Индексация по умолчанию начинается с нуля, но может быть изменена пользователем в настройках документа. Это особенно важно при импорте данных или работе с математическими моделями, где требуется согласованность индексации.

Для выполнения операций сложения, умножения, транспонирования и вычисления определителя используются стандартные обозначения: +, *, T (транспонирование), det(A). Стоит учитывать, что Mathcad автоматически проверяет размерность матриц при выполнении операций и выдаёт предупреждение при несоответствии. Это позволяет избегать логических ошибок при построении численных моделей.

Инструмент augment объединяет матрицы по строкам или столбцам, а submatrix – извлекает подматрицы, что удобно при работе с блочными структурами. Для решения систем линейных уравнений применяется оператор обратной матрицы A^–1 или функция lsolve, если необходимо использовать метод Гаусса без явного нахождения обратной матрицы.

Mathcad поддерживает символьные и численные методы, что позволяет анализировать поведение матриц при различных параметрах. Использование переменных с последующим автоматическим обновлением всех зависимых вычислений делает среду особенно удобной для параметрических исследований и оптимизации.

Создание и инициализация матриц в Mathcad

Для создания матрицы в Mathcad используйте квадратные скобки или инструмент «Insert Matrix». При вводе вручную применяются двойные щелчки клавиш: нажмите [Ctrl]+[M], чтобы вставить матрицу заданных размеров. Далее последовательно вводятся элементы по строкам слева направо, затем переход осуществляется на следующую строку.

Размер матрицы задается в момент вставки: указывается количество строк и столбцов. После создания доступна точечная модификация элементов по индексам. Нумерация по умолчанию начинается с 0. Если требуется изменить начальный индекс, выполните настройку в Math > Matrix > Default Indexing.

Инициализировать матрицу можно с помощью программной области или выражений. Например, присваивание A := matrix(3, 3) создаёт матрицу 3×3, заполненную нулями. Для заполнения значениями используйте оператор subscript: A[0,1 := 5 присваивает значение 5 элементу во второй колонке первой строки.

Массив можно инициализировать функцией: A[i, j := i + j задаёт зависимость элементов от их индексов. Это удобно при генерации симметричных или параметрических матриц. Также применимы векторы: v := 0..5 создаёт вектор из шести элементов. Для преобразования в столбец используйте транспонирование: v^T.

Инициализация числовыми последовательностями осуществляется с помощью диапазонов. Например, i := 1..10 формирует вектор строку, который можно использовать как базу для построения матриц через вложенные циклы или программный блок с оператором for.

Сложение и вычитание матриц с различными размерами

В Mathcad невозможно напрямую выполнять сложение или вычитание матриц, имеющих разные размеры. Такие операции приводят к ошибке: «Матрицы имеют несовместимые размеры». Для корректной работы необходимо привести матрицы к одинаковой размерности.

Определите размеры каждой матрицы с помощью встроенной функции rows(A) и cols(A).
Если размеры не совпадают, используйте функции дополнения:
- Создайте новую матрицу с нужными размерами с помощью matrix(m, n).
- Скопируйте элементы меньшей матрицы в новую с помощью циклов for или индексации.
- Оставшиеся ячейки заполните нулями или другим нейтральным значением.
После выравнивания размеров выполните стандартное сложение или вычитание: C := A + B или C := A - B.

Альтернативный подход – обрезка большей матрицы до размеров меньшей. Это актуально, если важны только совпадающие области:

Создайте новую матрицу нужного размера.
Скопируйте только соответствующие элементы из исходной матрицы.

Используйте программируемые блоки (Programming) для автоматизации приведения размеров. Пример функции дополнения матрицы до нужного размера:


PadMatrix(A, m, n) :=
begin
M := matrix(m, n)
for i ∈ 0..rows(A)-1
for j ∈ 0..cols(A)-1
M[i, j := A[i, j
return M
end

Обработка несовпадающих размеров должна быть преднамеренной. Автоматическое выравнивание без понимания контекста может привести к искажению данных.

Умножение матриц и работа с транспонированными формами

В Mathcad для умножения матриц используется оператор умножения *. Размерности должны быть согласованы: число столбцов первой матрицы должно совпадать с числом строк второй. Например, при перемножении матрицы A размером 3×2 и матрицы B размером 2×4 результатом будет матрица 3×4. Несогласованные размерности вызывают ошибку вычислений.

Для транспонирования матрицы применяется апостроф '. Выражение A' возвращает транспонированную матрицу: строки становятся столбцами, и наоборот. Это важно при симметризации выражений, а также при вычислении произведений типа A' * A в методах наименьших квадратов.

При работе с векторами следует учитывать: в Mathcad по умолчанию создаются столбцы. Чтобы получить строку, необходимо транспонировать вектор. Так, если v – вектор-столбец, то v' – вектор-строка, пригодный для скалярного произведения.

Умножение транспонированных матриц используется в задачах оптимизации, обработки сигналов и машинного обучения. Например, при вычислении ковариационной матрицы используется операция X' * X, где X – матрица признаков. Результат – квадратная симметричная матрица, отражающая взаимосвязи между признаками.

Mathcad позволяет комбинировать обычное и поэлементное умножение. Для поэлементного произведения транспонированных матриц применяйте оператор .: A' . B. Это особенно полезно в численных методах, где требуется операция над соответствующими элементами без суммирования по строкам и столбцам.

Обратная матрица и определитель: вычисление и ошибки

Для вычисления обратной матрицы в Mathcad используется функция invert(A), где A – квадратная матрица. Обязательное условие: матрица должна быть невырожденной, то есть её определитель не равен нулю.

Определитель вычисляется с помощью функции det(A). Если результат близок к нулю (например, 1·10^-14), Mathcad может интерпретировать матрицу как вырожденную из-за ограничений машинной точности. Это часто происходит при работе с численно нестабильными матрицами или при наличии линейно зависимых строк/столбцов.

Перед обращением матрицы необходимо проверять её обусловленность. Для этого используют cond(A) – число обусловленности. Если cond(A) > 10¹⁰, то матрица считается плохо обусловленной, и обратная может содержать значительные численные ошибки.

Mathcad не выдаёт ошибку при вычислении invert(A) для плохо обусловленной матрицы, но результат может быть бесполезен. Рекомендуется предварительно нормализовать данные или использовать устойчивые методы решения, например, сингулярное разложение (svd(A)), если требуется устойчивое обращение.

При вычислении определителя больших матриц возможны ошибки округления. Mathcad применяет алгоритмы с использованием LU-разложения, чувствительные к накоплению погрешностей. Для точных символьных расчётов лучше применять режим символьной математики через det(A)→.

Нельзя применять invert(A) к прямоугольным матрицам. Для псевдообратной матрицы следует использовать lsolve(A, b) или svd-основанные методы. Это особенно актуально в задачах регрессии и аппроксимации.

Применение встроенных функций для анализа матриц

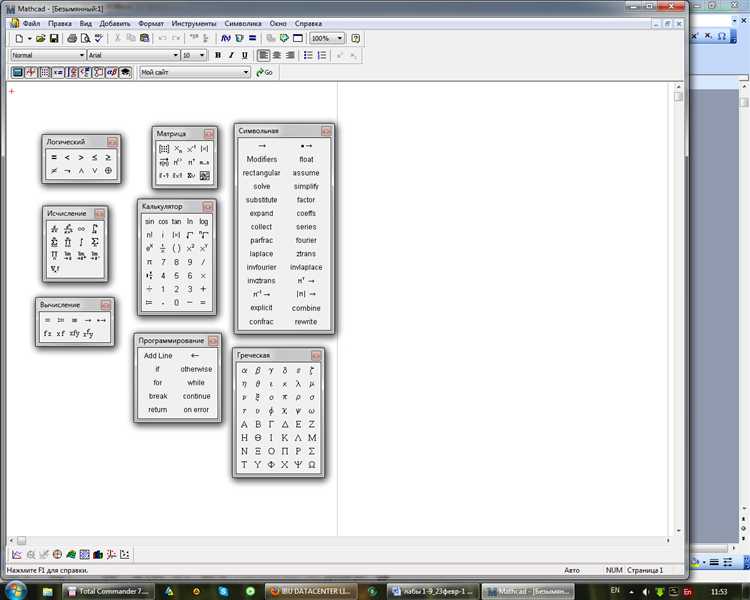
Mathcad предоставляет набор встроенных функций, существенно упрощающих анализ матриц. Для вычисления определителя используйте функцию det(A), где A – квадратная матрица. Например, det([[2, 3], [1, 4]]) возвращает 5. Эта функция необходима при проверке невырожденности матриц.

Для поиска обратной матрицы применяйте inverse(A). Mathcad автоматически проверяет, существует ли обратная матрица, и выдаёт ошибку, если det(A) = 0. Аналогичное действие выполняет возведение в степень A^-1.

Функция eigvec(A) возвращает матрицу собственных векторов, а eigval(A) – соответствующие собственные значения. Это критично при диагонализации и спектральном анализе. Убедитесь, что A – квадратная, иначе функции не сработают.

Для нахождения следа матрицы используйте tr(A). Это полезно при оценке характеристического полинома и проверке сохранения инвариантов при преобразованиях.

Анализ ранга производится с помощью rank(A). Это важно при определении линейной зависимости строк и столбцов. При работе с переопределёнными системами уравнений эта функция помогает оценить количество независимых уравнений.

Функция cond(A) вычисляет число обусловленности. Это ключевой показатель при оценке устойчивости численных решений. Значения, близкие к единице, указывают на хорошую обусловленность, тогда как большие значения свидетельствуют о высокой чувствительности к погрешностям.

Проверку симметричности матрицы можно выполнить с помощью логического сравнения: A = transpose(A). Это особенно важно при работе с матрицами ковариации и решениями симметричных систем уравнений.

Решение систем линейных уравнений с использованием матриц

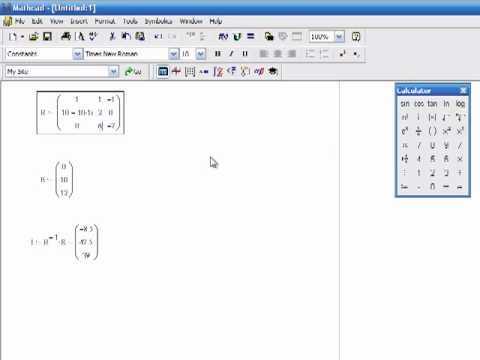
В Mathcad решение систем линейных уравнений реализуется через матричные операции, что позволяет существенно упростить вычислительный процесс и минимизировать ошибки. Для системы уравнений вида Ax = b, где A – матрица коэффициентов, x – вектор неизвестных, а b – вектор свободных членов, ключевой инструмент – обратная матрица A⁻¹.

Вычисление решения сводится к операции умножения обратной матрицы на вектор свободных членов: x = A⁻¹b. В Mathcad оператором обратной матрицы является символ ^-1, например, A^-1. При этом важно убедиться, что матрица A невырождена (det(A) ≠ 0), иначе обратная матрица не существует.

Для проверки невырожденности применяйте функцию det(A). Значение, близкое к нулю, свидетельствует о возможной сингулярности, что потребует использования альтернативных методов решения, например, псевдообратной матрицы или численных алгоритмов.

Mathcad поддерживает встроенную функцию solve(A, b) для автоматического нахождения решения без явного вычисления обратной матрицы. Этот способ эффективен при больших размерностях и снижает влияние численных ошибок.

При решении систем с параметрами рекомендуется использовать параметрические выражения и функцию solve для аналитического или численного определения векторов решений, что упрощает анализ зависимости результата от входных данных.

Для повышения точности в вычислениях с матрицами используйте встроенные числовые типы с повышенной точностью, избегайте преобразований типов и контролируйте масштаб коэффициентов, чтобы минимизировать накопление ошибок.

Вопрос-ответ:

Как в Mathcad задать матрицу и какие способы ввода доступны?

В Mathcad можно создавать матрицы несколькими способами. Самый распространённый — вручную вводить элементы, располагая их в ячейках через точку с запятой для строк и запятую для столбцов. Также можно использовать встроенные функции, например, `matrix(rows, cols, formula)`, чтобы автоматически задать элементы. Можно импортировать матрицу из внешних источников или скопировать её из другого документа Mathcad.

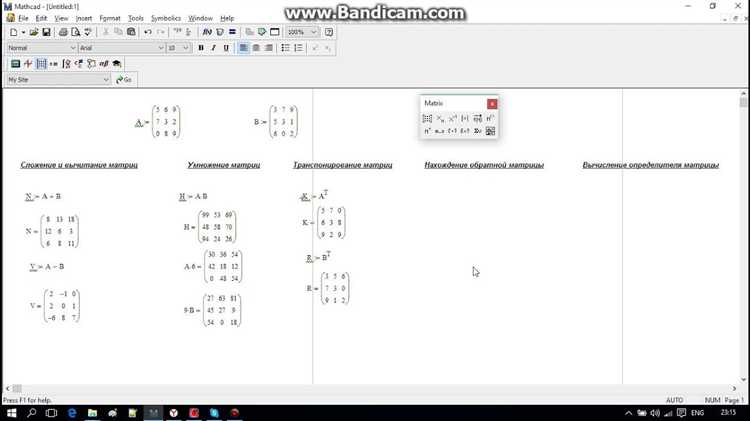
Какие базовые операции с матрицами поддерживает Mathcad и как они выполняются?

Mathcad позволяет выполнять сложение, вычитание, умножение матриц, транспонирование, нахождение обратной матрицы и определителя. Для сложения и вычитания достаточно использовать знаки «+» и «-» между матрицами одинаковых размеров. Умножение матриц происходит по стандартным правилам линейной алгебры с помощью оператора умножения. Функция `transpose()` возвращает транспонированную матрицу, а `det()` — определитель. Обратную матрицу вычисляет функция `inverse()`.

Как проверить совместимость матриц для умножения в Mathcad?

В Mathcad умножение матриц возможно, если число столбцов первой матрицы совпадает с числом строк второй. Чтобы проверить это, можно вывести размеры матриц с помощью функции `rows()` и `cols()` и сравнить их. Если условие не выполняется, Mathcad выдаст ошибку при попытке умножения.

Можно ли в Mathcad выполнять операции с разреженными матрицами и как это реализуется?

Mathcad не содержит специальных встроенных функций для работы с разреженными матрицами, как это делают некоторые специализированные программы. Тем не менее, можно использовать стандартные методы хранения данных, создавая матрицы с большим количеством нулевых элементов и применяя фильтры или условия для операций только над ненулевыми значениями. Для оптимизации можно использовать пользовательские скрипты или экспорт данных в более специализированные среды.

Как в Mathcad найти собственные значения и собственные векторы матрицы?

Для вычисления собственных значений и собственных векторов в Mathcad используется функция `eigenvals()` для значений и `eigenvecs()` для векторов. Эти функции принимают квадратную матрицу и возвращают соответствующие наборы. Результаты можно использовать для дальнейшего анализа или решения систем уравнений. Важно, чтобы матрица была числовой и квадратной.

Как выполнить умножение двух матриц в Mathcad и какие ошибки могут возникнуть при этом?

В Mathcad умножение матриц происходит с помощью оператора умножения «*». Для корректного умножения размерность матриц должна соответствовать: число столбцов первой матрицы должно совпадать с числом строк второй. Если размеры не подходят, программа выдаст ошибку. Например, если матрица A размером 3×2, а матрица B – 2×4, то произведение A*B будет иметь размер 3×4. В случае попытки умножить матрицы с несовместимыми размерами Mathcad сообщит о несоответствии размерностей, и результат не будет вычислен.

Какими способами можно найти обратную матрицу в Mathcad и что делать, если матрица необратима?

Для поиска обратной матрицы в Mathcad используется оператор обратной матрицы — символ «^(-1)». Например, если матрица обозначена как A, то обратная будет A^(-1). Однако обратная существует только для квадратных матриц с ненулевым определителем. Если матрица вырождена (определитель равен нулю), Mathcad выдаст предупреждение или ошибку, и обратную найти нельзя. В таких случаях для решения задач можно использовать псевдообратную матрицу, вычисляемую с помощью функции pseudoinverse, или применять методы разложения, например, сингулярное разложение, если это поддерживается.