Какие трехмерные графики существуют в mathcad

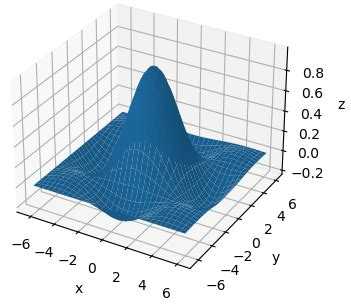
Mathcad предоставляет несколько типов трехмерных графиков, каждый из которых оптимален для визуализации различных математических и инженерных задач. Основные виды включают поверхностные графики, сеточные графики и точечные облака. Каждый тип имеет собственные параметры настройки, влияющие на точность и наглядность представления данных.

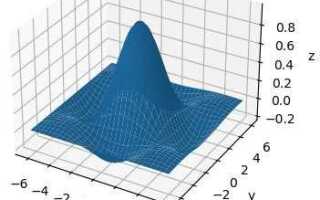
Поверхностные графики удобны для отображения функций двух переменных, позволяя оценивать непрерывность и изменения параметров по обеим осям. Особое внимание стоит уделять настройке разбиения сетки, поскольку от этого зависит детализация и плавность поверхности. В Mathcad возможно управление цветовой палитрой и уровнем прозрачности, что улучшает восприятие сложных поверхностей с несколькими экстремумами.

Сеточные графики представляют собой трехмерные линии, соединяющие точки по осям X и Y. Они эффективны для анализа распределения данных и выявления аномалий. Важным аспектом является выбор типа интерполяции между узловыми точками, так как это напрямую влияет на точность визуализации.

Точечные облака применяются для представления разрозненных данных в пространстве, часто используемых при обработке экспериментальных результатов. Mathcad позволяет менять размер и цвет точек для выделения определенных групп или областей данных.

Выбор конкретного вида трехмерного графика в Mathcad должен основываться на целях анализа и характеристиках исходных данных. Правильная настройка параметров визуализации существенно повышает информативность графика и облегчает последующую интерпретацию результатов.

Построение поверхностей: типы и возможности настройки

В Mathcad доступны несколько видов поверхностей для визуализации трехмерных функций: поверхности по сетке (mesh surfaces), сплошные поверхности (solid surfaces) и контурные поверхности (contour surfaces). Каждый тип отличается способом отображения и параметрами настройки.

Поверхности по сетке создаются на основе дискретной сетки узлов с последующим соединением точек линиями. Это позволяет четко видеть структуру сетки и грани. Рекомендуется использовать при анализе гладких функций с равномерным распределением узлов. Можно менять плотность сетки через количество шагов по осям, что влияет на детализацию и быстродействие построения.

Сплошные поверхности отображают непрерывную заливку между узлами, что улучшает восприятие объема и формы объекта. Для повышения реалистичности доступны параметры освещения, прозрачности и цветового градиента. Использование градиентных цветов помогает визуально выделять зоны с резкими изменениями функции.

Контурные поверхности сочетают 3D-модель с наложением горизонтальных линий уровней. Такой вид удобен для анализа изолиний и точного определения значений функции на различных высотах. Настройка толщины и цвета линий позволяет сделать изображение более информативным.

В настройках всех типов поверхностей можно изменять масштаб по осям, задавать диапазоны построения и режимы интерполяции. Интерполяция влияет на гладкость и точность изображения, рекомендуется использовать метод билинейной или бикубической интерполяции для получения оптимального баланса между качеством и скоростью.

Mathcad поддерживает экспорт графиков с сохранением параметров визуализации, что упрощает интеграцию результатов в отчеты и презентации. Для комплексного анализа рекомендуется комбинировать несколько типов поверхностей, чтобы подчеркнуть ключевые особенности функции.

Использование сеточных графиков для визуализации данных

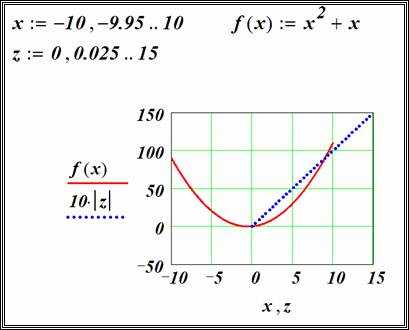
Сеточные графики в Mathcad представляют собой мощный инструмент для отображения функций двух переменных в виде поверхности, определенной на регулярной сетке. Они строятся на основе двумерных массивов значений, что позволяет получить детализированное изображение изменений функции в пространстве.

Для корректного построения необходимо задать сетку координатных точек по осям X и Y с равномерным шагом. Mathcad автоматически соединяет эти точки, формируя полигоны, создающие поверхность. Это облегчает анализ локальных максимумов, минимумов и седловых точек.

При работе с большими объемами данных рекомендуется выбирать оптимальный шаг сетки: слишком мелкий шаг увеличивает время вычисления и нагрузку на систему, а слишком крупный снижает точность визуализации. Практический диапазон шага – от 0,01 до 0,1, в зависимости от масштабов функции и цели анализа.

Важным преимуществом сеточных графиков является возможность применения цветовой заливки, которая в Mathcad может отражать значения функции или производные, облегчая восприятие градиентов и изменений. Для повышения читаемости рекомендуется использовать палитры с плавными переходами цветов.

Mathcad позволяет задавать параметры отображения сеточного графика, включая угол обзора и масштабирование, что помогает подчеркнуть ключевые особенности поверхности. Также возможно совмещение сеточного графика с другими типами 3D-графиков для комплексного анализа.

Для создания сеточного графика используется функция, принимающая на вход матрицы координат и значений функции. Важно следить за правильностью размерностей матриц и их синхронизацией, иначе визуализация будет искажена.

Использование сеточных графиков эффективно при исследовании непрерывных функций, решении задач оптимизации и моделировании физических процессов, где важна пространственная интерпретация данных. В Mathcad они обеспечивают удобство настройки и точность отображения, что делает их незаменимым инструментом при инженерном анализе.

Области применения объемных графиков с заливкой

Объемные графики с заливкой в Mathcad позволяют визуализировать сложные многомерные зависимости, обеспечивая наглядное восприятие распределения значений и взаимодействия параметров. Их используют в следующих сферах:

• Анализ функций нескольких переменных: визуализация поверхности позволяет выявлять экстремумы, седловые точки и области монотонности. Заливка цветом помогает четко выделять зоны с разным уровнем функции.
• Моделирование физических процессов: в теплообмене, гидродинамике и электромагнетизме объемные графики демонстрируют распределение температуры, давления или потенциала в трехмерном пространстве.
• Оптимизация и многокритериальный анализ: графики с цветовой заливкой показывают области допустимых решений и оптимумы при нескольких ограничениях, что облегчает визуальный выбор параметров.
• Обработка данных в инженерии: для оценки характеристик материалов и конструкций по нескольким параметрам заливка помогает быстро выделить критические зоны и тенденции.
• Экономическое моделирование: объемные графики применяют для отображения зависимостей доходов, затрат и объемов производства, где цветовые градации указывают на прибыльность или риски.

Рекомендации по использованию:

1. Подбирайте градации заливки с учетом контрастности и восприятия цвета, чтобы избежать визуального смешения важных областей.
2. Используйте прозрачность заливки для наложения нескольких поверхностей без потери информации.
3. Для сложных моделей разбивайте график на отдельные области с разными параметрами заливки, чтобы повысить читаемость.
4. Применяйте анимацию изменения параметров, если Mathcad-версия поддерживает, для динамического анализа зависимостей.

Особенности построения линий уровня и их интерпретация

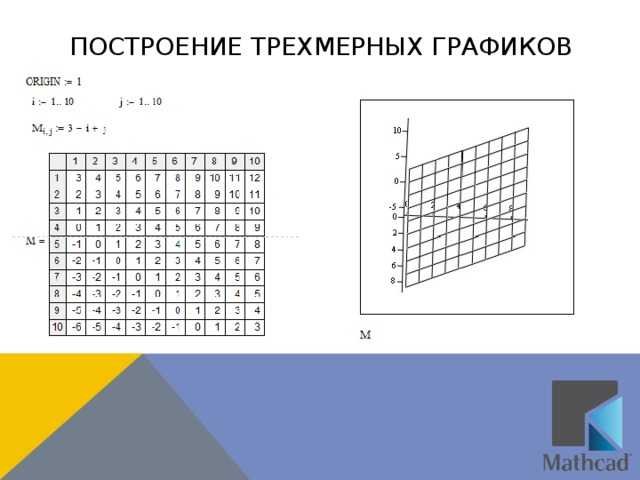
Линии уровня (контурные линии) в Mathcad служат для визуализации срезов трехмерной поверхности на постоянных значениях функции. Их построение требует точного задания сетки и корректной интерполяции между узлами.

• Для построения линий уровня в Mathcad необходимо задать двумерную сетку координат (X, Y) и вычислить значения функции Z = f(X, Y) на этой сетке.
• Рекомендуется использовать равномерно распределённые значения X и Y для обеспечения равномерного покрытия области и минимизации искажений.
• Mathcad автоматически строит линии уровня по заданным значениям функции, однако рекомендуется явно указывать уровни контуров через параметры графика для контроля детализации.
• Чем плотнее уровни линий, тем точнее отражаются мелкие изменения поверхности, но излишняя плотность усложняет восприятие.

Интерпретация линий уровня базируется на анализе их формы и расположения:

1. Плотно расположенные линии свидетельствуют о крутых градиентах функции и резких перепадах высоты.
2. Замкнутые линии уровня указывают на локальные экстремумы: внутренние выпуклости – минимумы, вогнутые – максимумы.
3. Параллельные и равномерно распределённые линии уровня соответствуют равномерному наклону поверхности.
4. Изломы или резкие изменения направления линий указывают на особенности поверхности, например, седловые точки.

Практические рекомендации при работе с линиями уровня в Mathcad:

• Используйте функцию contour с явным указанием векторов уровней для точного контроля отображения.
• Проверяйте адекватность сетки: слишком грубая сетка искажает линии, слишком мелкая увеличивает время вычислений.
• Сопоставляйте линии уровня с трехмерным графиком для проверки согласованности визуализации.
• В случае сложных поверхностей разбивайте область на участки для локального анализа линий уровня.

Создание трехмерных графиков функций с несколькими переменными

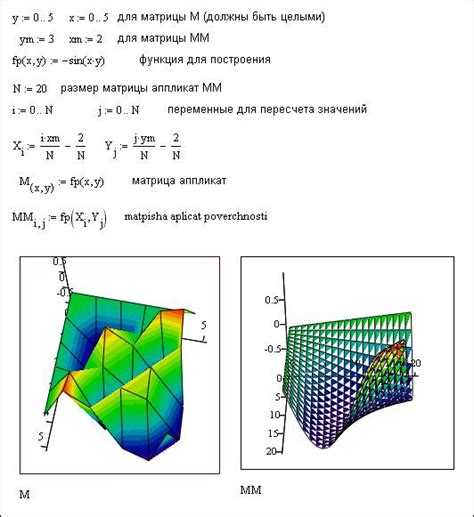
В Mathcad построение трехмерных графиков функций с двумя и более переменными реализуется через задание двумерной сетки значений аргументов и вычисление значений функции на этой сетке. Для этого применяются встроенные операторы создания массивов и двумерных матриц.

Первым этапом задаются диапазоны переменных с помощью оператора «:=» и функции распределения значений, например, с использованием выражения вида x := 0, 0.1 .. 10, где создается вектор с шагом 0.1 от 0 до 10. Аналогично задается второй аргумент y.

Далее формируется двумерная сетка значений через функцию meshgrid(x, y), которая возвращает два массива одинакового размера, соответствующие координатам по осям X и Y для каждого узла сетки.

Функция вычисляется как матричная операция, где для каждого элемента сетки определяется значение функции Z: z := f(X, Y). Mathcad автоматически применяет функцию покомпонентно, если она корректно определена для матриц.

Для визуализации используется инструмент 3D-графиков, где в настройках указывается источник данных – массивы X, Y и Z. Можно настроить параметры отображения: цветовые карты, прозрачность, тип сетки (поверхность, каркас), а также угол обзора для удобного анализа.

Рекомендуется избегать слишком плотных сеток, чтобы не перегружать вычисления и интерфейс. Оптимальный шаг сетки зависит от характера функции, но обычно значения в пределах 50–100 точек по каждой оси обеспечивают баланс между точностью и производительностью.

Для сложных функций с особенностями в отдельных областях полезно применять локальную детализацию сетки, создавая неоднородные векторы аргументов с уменьшенным шагом в интересующих зонах.

Также Mathcad позволяет строить 3D-графики с параметрическими функциями нескольких переменных, что расширяет возможности моделирования и анализа сложных объектов.

Настройка отображения осей и масштабов в 3D графиках Mathcad

В Mathcad управление осями в трехмерных графиках реализовано через параметры, задаваемые в свойствах графика. Для настройки отображения осей используются функции и диалоговые окна, позволяющие точно задать диапазоны, шаги и подписи.

Диапазон осей X, Y и Z задается через свойства графика, где можно вручную указать минимальное и максимальное значение каждой оси. Это позволяет исключить автоматическое масштабирование, которое часто не подходит при анализе данных с нестандартными диапазонами. Значения вводятся в полях «Min» и «Max» для каждой оси.

Шаг сетки осей регулируется отдельными параметрами, что помогает контролировать плотность разметки. Оптимальный выбор шага обеспечивает четкую читаемость без излишней загруженности графика. Для этого рекомендуется подбирать шаг, кратный диапазону оси с учётом особенностей визуализируемой функции.

Подписи осей в Mathcad можно изменить, используя свойства надписей, где задаются как текстовые метки, так и их расположение. Кроме того, поддерживается форматирование числовых меток, включая количество знаков после запятой и экспоненциальное представление.

Масштаб осей можно настроить не только через числовые границы, но и применением коэффициентов масштабирования по отдельным осям. Это важно при визуализации данных с разными размерностями, чтобы избежать искажений формы графика.

Для более детального контроля существует возможность программного управления осями с помощью встроенных функций Mathcad. Например, функция plot3d позволяет указывать параметры осей в скриптовом режиме, что полезно при автоматизации построения графиков.

При работе с трехмерными графиками рекомендуется фиксировать масштаб по крайней мере по одной оси, чтобы сохранить постоянство визуального восприятия при повороте графика. Для этого следует использовать опцию закрепления диапазона оси в свойствах графика.

Кроме стандартных настроек, в Mathcad можно включать или отключать отображение сетки, что влияет на восприятие масштаба и упрощает ориентирование в трехмерном пространстве. Настройка цвета и стиля линий сетки доступна через свойства графика и помогает выделить важные участки.

В итоге, точная настройка осей и масштабов в Mathcad достигается путем комплексного использования параметров диапазонов, шагов, подписей и масштабных коэффициентов, что обеспечивает максимально информативное и удобное для анализа визуальное представление трехмерных данных.

Импорт и экспорт трехмерных графиков для дальнейшего анализа

Mathcad поддерживает экспорт трехмерных графиков в форматы, совместимые с CAD и специализированными программами анализа, такими как DXF, SVG и CSV. Для сохранения точности геометрии рекомендуется использовать формат DXF, который сохраняет координаты точек и структуру поверхности. При экспорте графика в CSV сохраняются только числовые данные, что позволяет выполнять последующую обработку в статистических и вычислительных пакетах.

Для импорта трехмерных данных в Mathcad допустимы форматы CSV и TXT с координатами в столбцах. Важно придерживаться стандартизированной структуры данных: каждый столбец – это координата X, Y и Z. Mathcad автоматически формирует поверхность или облако точек на основе таких данных. Для корректной визуализации необходимо убедиться, что координаты упорядочены по сетке или представлены в виде точечного набора с известной топологией.

Экспорт в форматы векторной графики, например SVG, позволяет интегрировать 3D-графики в техническую документацию с возможностью масштабирования без потери качества, но не подходит для вычислительного анализа. В случаях, когда требуется обмен данными с CAD-системами, предпочтительнее использовать DXF с сохранением слоя и цветов.

Рекомендуется перед экспортом проверить разрешение и детализацию графика в Mathcad, поскольку чрезмерно высокая плотность точек увеличивает размер файла и затрудняет обработку в других приложениях. Оптимальный баланс достигается с помощью параметров дискретизации поверхности.

Импортированные трехмерные данные лучше всего предварительно очистить от выбросов и нормализовать по масштабу для соответствия единицам измерения Mathcad. Это обеспечит корректное построение и точность последующего анализа.

Вопрос-ответ:

Какие типы трехмерных графиков доступны в Mathcad для визуализации данных?

В Mathcad представлены несколько видов трехмерных графиков, включая поверхностные графики, графики точек, линейные 3D-графики и контурные поверхности. Каждый тип подходит для разных задач: например, поверхностные графики отображают изменения функции по двум переменным, а графики точек показывают отдельные значения в трехмерном пространстве.

Каковы особенности построения поверхностных графиков в Mathcad?

Поверхностные графики в Mathcad строятся на основе двух переменных, задающих координаты по осям X и Y, а третья переменная определяет высоту поверхности по оси Z. Для создания такого графика необходимо определить область значений переменных и вычислить функцию на сетке этих значений. Результат визуализируется как непрерывная поверхность с возможностью вращения и масштабирования для более удобного анализа.

Можно ли в Mathcad создавать анимированные трехмерные графики, и как это реализуется?

В базовой версии Mathcad анимация 3D-графиков не предусмотрена напрямую, однако пользователи могут добиться эффекта анимации, изменяя параметры графика через циклы или слайдеры, чтобы пошагово отображать изменение формы графика. Это позволяет визуально проследить динамику изменения функции в трехмерном пространстве.

Как влияют настройки визуализации на восприятие трехмерных графиков в Mathcad?

Настройки визуализации, такие как освещение, угол обзора, цветовая гамма и прозрачность поверхности, существенно меняют восприятие графика. Правильно подобранные параметры помогают лучше понять структуру данных, выявить особенности формы и выявить важные области на графике. Mathcad предоставляет инструменты для удобного изменения этих параметров в интерактивном режиме.

В каких случаях лучше использовать контурные 3D-графики вместо поверхностных?

Контурные графики показывают линии равных значений функции на плоскости XY и применяются для анализа уровней функции без отображения полного объема поверхности. Они удобны, когда важно изучить распределение значений и найти экстремумы или области с одинаковыми параметрами, особенно если трехмерная поверхность слишком сложна для восприятия или избыточна для задачи.