Какие виды функции в mathcad вам известны

Mathcad предоставляет широкий спектр встроенных функций, охватывающих численные вычисления, символьную математику, статистику, работу с матрицами и обработку сигналов. Каждая категория функций имеет специфическое применение, что позволяет точно и эффективно решать инженерные задачи разной сложности.

Арифметические и алгебраические функции используются для базовых вычислений и трансформаций выражений: abs() – модуль, sqrt() – корень, exp() – экспонента. Эти функции часто применяются при построении математических моделей физических процессов.

Тригонометрические функции, включая sin(), cos(), tan(), и их обратные аналоги, актуальны при расчетах колебательных систем, анализа сигналов и векторной алгебры. Они работают с аргументами в радианах, что следует учитывать при вводе данных.

Статистические функции позволяют проводить анализ выборок и распределений: mean() – среднее значение, stdev() – стандартное отклонение, rand() – генерация случайных чисел. Эти функции важны в задачах обработки экспериментальных данных и построения моделей неопределенности.

Логические и условные функции управляют потоком вычислений: if, else, otherwise. Они позволяют реализовывать алгоритмы с ветвлением, что критично для адаптивных расчетов и итерационных методов.

Функции для работы с матрицами включают inv() – обращение, transpose() – транспонирование, det() – определитель. Эти инструменты необходимы при решении систем линейных уравнений и векторно-матричном моделировании.

Пользовательские функции позволяют создавать собственные определения с помощью ключевого слова :=. Это особенно полезно при повторяющихся вычислениях или автоматизации рутинных задач в расчетных шаблонах.

Грамотное использование встроенных и пользовательских функций в Mathcad позволяет сократить объем ручных расчетов, повысить точность и обеспечить прозрачность математических моделей в инженерных проектах.

Как создавать пользовательские функции в Mathcad

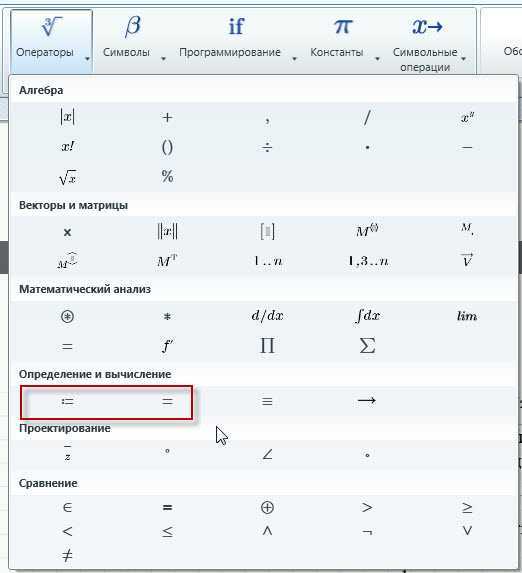
Пользовательские функции в Mathcad позволяют создавать переиспользуемые блоки вычислений с произвольными входными параметрами. Это особенно полезно при работе с повторяющимися расчетами или при необходимости структурировать сложные модели.

Введите имя функции с последующим списком аргументов в круглых скобках. Пример: f(x, y).
После нажатия клавиши = введите выражение, определяющее тело функции. Пример: f(x, y) := x² + y².
Mathcad автоматически интерпретирует это как определение функции, доступной для дальнейших вычислений.

Функция может использовать как численные значения, так и массивы, единицы измерения, логические выражения и встроенные операторы. Для повышения гибкости допускается использование вложенных пользовательских функций.

Функции можно размещать в любом месте рабочего листа, но для корректного выполнения вызовов они должны быть определены до использования.
Имена функций чувствительны к регистру. f(x) и F(x) – разные функции.
Для определения многослойной логики можно использовать управляющие конструкции: if, otherwise.

Mathcad не требует предварительного объявления типов аргументов. Однако рекомендуется использовать поясняющие комментарии рядом с определением функции для документирования её назначения и ожидаемых типов входных данных.

Для повторного использования функций между проектами сохраните их в виде пользовательских библиотек. Это делается через файл с расширением .xmcd или .mcdx, который можно подключать к другим рабочим листам через команду Insert > Reference.

Применение встроенных математических функций для инженерных расчётов

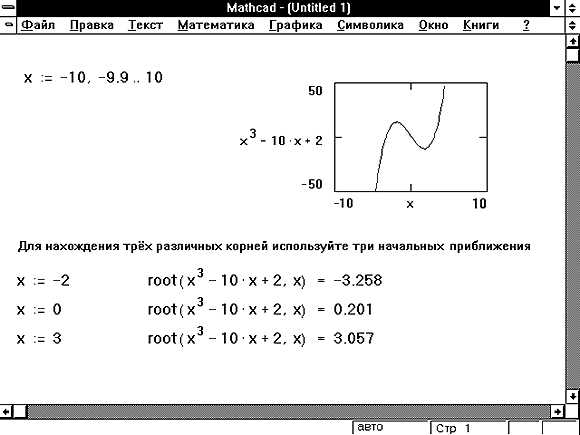
Mathcad предоставляет обширный набор встроенных математических функций, оптимизированных под задачи инженерного анализа. Для численного интегрирования используется функция int(f, a, b), обеспечивающая точные результаты при работе с экспериментальными данными или моделированием физических процессов. Например, расчёт расхода жидкости через сечение с переменным давлением можно выполнить напрямую без прибегания к численным методам вручную.

Функции линейной алгебры, такие как inv(A), det(A) и eig(A), позволяют быстро анализировать устойчивость систем, решать СЛАУ и определять собственные значения в задачах динамики. Это критично при расчёте колебаний и оценке надёжности конструкций.

Для инженерных расчётов с использованием регрессионного анализа и обработки статистических данных применяются функции linfit(x, y), mean(v), stdev(v). Они позволяют анализировать экспериментальные данные, определять тренды и прогнозировать поведение систем в зависимости от входных параметров.

Функции работы с комплексными числами, такие как re(z), im(z), abs(z), используются при моделировании электрических цепей переменного тока. Это позволяет проводить фазовые расчёты и анализировать характеристики цепей без необходимости вручную раскладывать выражения на составляющие.

Инженеры, работающие с дифференциальными уравнениями, могут применять функцию Odesolve для численного решения систем ОДУ. Это особенно важно в задачах теплопередачи, гидродинамики и автоматического регулирования, где аналитическое решение получить невозможно.

Применение встроенных функций ускоряет разработку инженерных решений, повышает точность расчётов и позволяет сосредоточиться на анализе результатов, а не на технических деталях вычислений.

Использование логических функций для построения условий

В Mathcad логические функции позволяют формировать условия, управляющие выполнением вычислений. Ключевые функции: if, otherwise, and, or, not, xor, isNaN, iseven, isodd.

Функция if используется для построения разветвлённой логики. Она требует обязательного указания условия и результата при его выполнении. Без otherwise условие действует строго, без альтернативы:

if(x > 0, sqrt(x))

Для полного ветвления применяется otherwise:

if(x > 0, sqrt(x), otherwise, 0)

Логические операторы and, or и not применяются для составных условий:

if(x > 0 and x <= 10, "в пределах")

Функции проверки состояния переменных:

isNaN(x) – возвращает true, если x не является числом;
iseven(n) и isodd(n) – проверяют чётность и нечётность соответственно.

Логические конструкции интегрируются в пользовательские функции:

f(x) := if(x < 0, -1, otherwise, 1)

Условные выражения можно использовать и в матрицах. Например, фильтрация значений:

M := if(A > 0, A, otherwise, 0)

При построении графиков логика применима для исключения участков с недопустимыми значениями. Пример – подавление отрицательных значений под корнем:

y(x) := if(x >= 0, sqrt(x), otherwise, NaN)

Рекомендуется использовать isNaN для проверки корректности промежуточных вычислений и отладки условий.

Функции работы с матрицами: ввод, преобразование и анализ

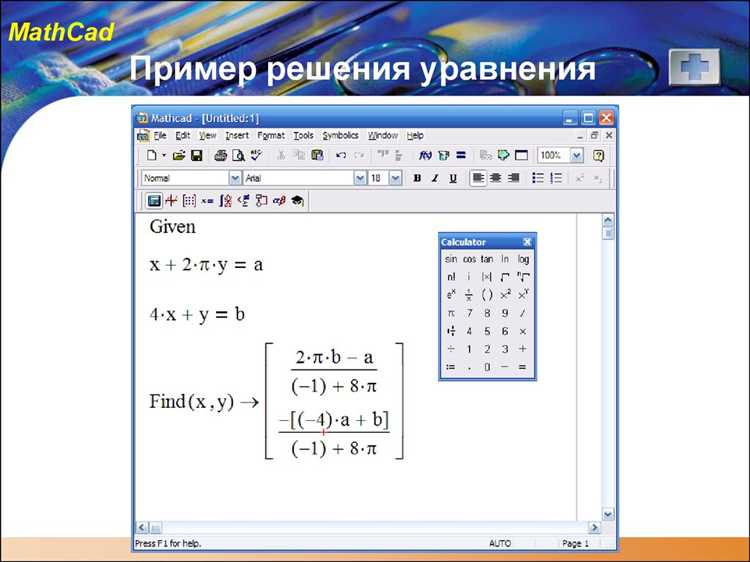
В Mathcad ввод матриц осуществляется через клавишу «Ctrl+M» или вставкой массива с указанием размерности. Элементы заполняются вручную или с помощью выражений. Для динамического формирования используется функция stack – она объединяет векторные или матричные элементы по вертикали, а augment – по горизонтали.

Преобразование матриц выполняется с применением встроенных функций. transpose(A) возвращает транспонированную матрицу. inv(A) – обратную, если матрица квадратная и невырожденная. Для определения ранга применяется rank(A), а diag(v) создает диагональную матрицу из вектора или извлекает диагональ из матрицы.

Для численного анализа используются функции: det(A) вычисляет определитель, trace(A) – след, norm(A) – норму. Функция eigenvals(A) возвращает собственные значения, а eigenvecs(A) – собственные векторы. При решении СЛАУ применяется lsolve(A, b) или оператор A⁻¹·b, если существует обратная матрица.

Матрицы могут фильтроваться и сортироваться. Для извлечения подматриц используется индексирование с диапазонами: A[0..1, 1..2]. Функция submatrix(A, m1, m2, n1, n2) позволяет точно задавать границы. Сортировку выполняет sort(v) для векторов или sortrows(A, col) по столбцу матрицы.

Все операции поддерживают символьный и численный режим. Символьное упрощение выражений с матрицами производится через кнопку «symbolic» или команду simplify. При необходимости используются float или exact для управления типом вычислений.

Функции для обработки и интерполяции табличных данных

Mathcad предоставляет набор функций, специально предназначенных для работы с табличными данными, включая их анализ, интерполяцию и извлечение значений по заданным параметрам. Эти функции позволяют эффективно обрабатывать массивы чисел, полученные из экспериментов или внешних источников.

interp(x, X, Y) – линейная интерполяция. Возвращает значение функции Y(x) на основе известных точек X и Y. Требование: массив X должен быть строго возрастающим.
linterp(x, X, Y) – упрощённая версия interp с более жёсткой проверкой на порядок X. Подходит для одноразовых операций в инженерных расчётах.
polyfit(X, Y, n) – аппроксимация табличных данных полиномом n-й степени. Используется при необходимости сгладить данные или построить аналитическое выражение по экспериментальным точкам.
regress(X, Y) – линейная регрессия для определения зависимости между X и Y. Возвращает коэффициенты линейного уравнения и статистику отклонения.
interp2(x, y, X, Y, Z) – двухмерная интерполяция по сетке данных. X и Y – одномерные массивы координат, Z – матрица значений. Полезна при анализе поверхностей.
lookup(X, Y, x) – поиск значения Y, соответствующего ближайшему значению X, меньшему или равному x. Применяется при работе с пошаговыми зависимостями и характеристиками материалов.
augment(A, B) – объединение массивов по горизонтали. Используется для компоновки табличных данных перед анализом или визуализацией.
stack(A, B) – вертикальное объединение массивов. Применяется для последовательной обработки или накопления данных.

Для повышения точности рекомендуется перед интерполяцией выполнять предварительную фильтрацию данных и проверку на монотонность. При работе с большими массивами – использовать векторизированные формы функций и избегать циклов.

Как применять символьные функции для аналитических решений

Символьные функции Mathcad позволяют получать точные аналитические выражения вместо численных приближений. Для этого введите исходное выражение или уравнение с помощью переменных, после чего используйте функции символьного дифференцирования, интегрирования или упрощения.

Для дифференцирования примените оператор diff, указывая функцию и переменную. Mathcad вернёт точную производную в символьном виде, что удобно при анализе сложных формул и нахождении критических точек.

Интегрирование реализуется через функцию int, позволяющую вычислить неопределённый или определённый интеграл. При необходимости можно задавать пределы интегрирования, получая аналитическое решение без перехода к численным методам.

Функция simplify упрощает полученные выражения, сокращая их и делая более удобочитаемыми, что помогает лучше понять структуру результата и выявить важные зависимости.

Для решения уравнений и систем используйте solve, задавая уравнения в символическом виде. Mathcad вернёт аналитическое решение, если оно существует, или формулы для последующего численного анализа.

Рекомендуется проверять корректность символьных выражений с помощью substitute, подставляя численные значения и сравнивая с результатами численных вычислений.

Таким образом, символьные функции позволяют эффективно работать с аналитическими задачами, сокращая время на ручные преобразования и обеспечивая точность решений.

Функции управления единицами измерения в расчётах

Mathcad поддерживает строгий контроль и автоматическое преобразование единиц измерения, что позволяет исключить ошибки при вычислениях с физическими величинами. Основные функции управления единицами сосредоточены на присвоении, преобразовании и контроле совместимости единиц.

Функция unit() назначает единицу измерения числовому значению, например, 5 unit("m") – длина 5 метров. Это гарантирует корректное использование значения в формулах с учётом размерности.

Преобразование между системами измерений выполняется через оператор преобразования единиц →. Например, выражение 10 unit("km") → "m" вернёт 10000 метров. Mathcad автоматически учитывает коэффициенты перевода, что упрощает работу с разными системами.

Для проверки совместимости используется функция compatible(), которая возвращает логическое значение. Это помогает предотвратить арифметические ошибки при попытке сложить или сравнить величины с несовместимыми единицами.

Функция unitbase() возвращает базовые единицы измерения для сложных выражений, что облегчает анализ и оптимизацию формул.

Рекомендуется всегда явно указывать единицы измерения при вводе данных и проверять их совместимость в промежуточных расчетах. Это повышает надёжность моделей и позволяет использовать встроенные средства Mathcad для автоматического контроля и преобразования единиц без дополнительного кода.

Вопрос-ответ:

Какие виды функций доступны в Mathcad для выполнения математических вычислений?

В Mathcad есть несколько типов функций, которые можно использовать для решения задач. Среди них — встроенные функции (например, тригонометрические, логарифмы, экспоненты), а также пользовательские функции, которые создаются самим пользователем для конкретных целей. Кроме того, доступны функции с несколькими переменными, а также функции, возвращающие вектор или матрицу. Каждая из них предназначена для разных видов вычислений и позволяет гибко работать с данными.

Как в Mathcad создавать собственные функции, и чем они отличаются от встроенных?

Создание пользовательских функций в Mathcad осуществляется через определение имени функции и списка аргументов, после чего прописывается тело функции с необходимыми вычислениями. Эти функции могут быть как простыми, так и сложными, включать условия и циклы. Главное отличие от встроенных функций — возможность адаптировать вычисления под специфические задачи, которых нет среди стандартного набора Mathcad. Пользовательские функции позволяют расширить функционал и автоматизировать повторяющиеся вычисления.

Можно ли в Mathcad использовать функции для работы с матрицами и какие именно?

Да, Mathcad поддерживает функции, работающие с матрицами и векторами. Среди них — функции для сложения, умножения, транспонирования, вычисления детерминанта, обратной матрицы, а также для решения систем линейных уравнений. Некоторые из этих функций встроены в программу, а также можно создавать свои собственные для выполнения специфических операций с матрицами. Это особенно удобно при обработке больших объемов данных и при выполнении инженерных расчетов.

Для чего нужны условные функции в Mathcad и как их применять?

Условные функции в Mathcad позволяют изменять ход вычислений в зависимости от заданных условий. Например, с помощью операторов if-then-else можно создавать функции, которые выдают разные результаты в зависимости от значений входных параметров. Это полезно при моделировании процессов с ветвлениями, при анализе различных сценариев или при реализации алгоритмов с различными вариантами исполнения. Использование таких функций помогает сделать вычисления более гибкими и адаптированными к реальным задачам.

Какие особенности у функций с несколькими аргументами в Mathcad?

Функции с несколькими аргументами позволяют одновременно обрабатывать несколько входных значений, что расширяет возможности моделирования и вычислений. В Mathcad при определении такой функции перечисляют все необходимые параметры, а внутри функции можно использовать эти аргументы для комплексных вычислений. Это удобно, когда результат зависит от нескольких переменных, и нужно получить итоговое значение или структуру данных, например, в инженерных расчетах или при анализе многомерных данных.

Какие типы функций поддерживает Mathcad и для чего они применяются?

Mathcad позволяет создавать несколько видов функций, среди которых основные — простые, определённые пользователем, а также встроенные. Простые функции используются для базовых математических операций и часто записываются с помощью стандартных операторов. Пользовательские функции дают возможность описывать более сложные алгоритмы и повторно использовать их в расчетах. Встроенные функции обеспечивают быстрый доступ к распространённым математическим операциям, например, тригонометрическим или статистическим. Каждая категория служит для упрощения работы с математическими выражениями и автоматизации расчетов.