Что означает в maple

Функции в Maple – это основа для построения сложных математических моделей и автоматизации вычислительных процессов. С их помощью можно задавать аналитические выражения, проводить численные расчёты, а также создавать процедуры, которые повторяют алгоритмы решения задач. В Maple функции бывают анонимными и именованными, что даёт гибкость при организации кода и упрощает повторное использование вычислений.

Особое внимание следует уделять синтаксису определения функций. В Maple для этого используется стрелочная запись (x -> выражение) и команда proc, позволяющая реализовать многоступенчатые алгоритмы с локальными переменными. Выбор метода зависит от задачи: для простых выражений предпочтительна стрелочная форма, для комплексных – процедуры.

Практическое применение функций охватывает широкий спектр – от аналитического дифференцирования и интегрирования до решения систем уравнений и оптимизации. Кроме того, использование встроенных функций в сочетании с пользовательскими расширяет возможности анализа и визуализации результатов. Рекомендуется структурировать код, разбивая вычисления на логические блоки с чётко определёнными функциями, что облегчает отладку и масштабирование проектов.

Создание и объявление пользовательских функций в Maple

Для нескольких параметров синтаксис аналогичен: g := (x, y) -> x^2 + y^2;. Здесь важно разделять параметры запятыми и учитывать порядок их использования в теле функции.

Функции могут содержать как простые выражения, так и комплексные блоки кода с операторами условного ветвления, циклами и локальными переменными. Для сложных функций применяется конструкция proc:

h := proc(x, y) local z; z := x + y; return z^2; end proc;

В этом формате внутри proc можно определить локальные переменные через local, которые не влияют на внешнее пространство имён. Результат возвращается с помощью return. Отсутствие явного return приводит к возврату последнего вычисленного выражения.

Для повышения читаемости и управления функциями рекомендуется придерживаться единообразного стиля объявления: простые функции – через стрелочную нотацию ->, а многооперационные – через proc.

Пользовательские функции можно использовать как самостоятельные вычислительные блоки или интегрировать в более сложные алгоритмы, вызывая их по имени с необходимыми аргументами.

Использование встроенных математических функций для вычислений

Maple предоставляет широкий набор встроенных функций, оптимизированных для точных и эффективных вычислений. Среди них – тригонометрические (sin, cos, tan), экспоненциальные (exp), логарифмические (ln, log), гиперболические (sinh, cosh) и специальные функции (gamma, erf). Для вызова функций достаточно использовать их стандартные имена с аргументом в скобках, например, sin(x) или ln(5).

Встроенные функции в Maple автоматически поддерживают работу с комплексными числами, что исключает необходимость дополнительного разложения. Например, вычисление exp(I*Pi) вернет точное значение -1 без приближений.

Для повышения точности вычислений можно задавать количество знаков с помощью команды evalf(f, n), где f – функция, n – число десятичных знаков. Встроенные функции при этом сохраняют аналитическую форму, а evalf осуществляет численное преобразование.

Maple позволяет комбинировать встроенные функции в сложных выражениях с поддержкой упрощения через simplify или expand. Например, simplify(sin(x)^2 + cos(x)^2) сразу вернет 1. Использование simplify улучшает интерпретацию результатов и оптимизирует вычисления.

Для численного интегрирования встроенные функции удобно применять совместно с int и evalf. Интеграл от exp(-x^2) по заданному диапазону можно вычислить как evalf(int(exp(-x^2), x=0..1)), что вернет численное значение с высокой точностью.

Встроенные функции поддерживают векторизацию, что позволяет применять их к спискам и матрицам через оператор map. Например, map(sin, [0, Pi/2, Pi]) выдаст список значений синуса для каждого элемента.

Использование встроенных математических функций в Maple сокращает время разработки, обеспечивает точность и расширяет возможности анализа, позволяя решать как простые, так и сложные вычислительные задачи без необходимости реализации собственных алгоритмов.

Параметризация функций и передача аргументов

В Maple параметризация функций выполняется через явное объявление переменных в заголовке функции с помощью синтаксиса proc или объявления анонимных функций с использованием стрелочного оператора (->). Например, f := (x,y) -> x^2 + y; определяет функцию с двумя параметрами.

Передача аргументов в функции может быть как позиционной, так и именованной. Позиционный способ требует строго соблюдать порядок аргументов: f(2,3). Именованная передача реализуется через структуру f(x=2,y=3), что повышает читаемость и гибкость вызова, особенно при большом числе параметров.

Для параметров можно задавать значения по умолчанию, используя конструкцию option remember или внутри тела функции, например: g := proc(x, y:=5) x+y end proc;. Это упрощает вызовы с пропущенными аргументами, сохраняя корректность вычислений.

При работе с параметризацией важно учитывать область видимости переменных. Локальные переменные объявляются через local внутри proc, что предотвращает конфликт с глобальными именами.

В Maple поддерживается передача аргументов по ссылке и значению в зависимости от типа данных и структуры. Например, изменения списков внутри функции отражаются вне её, если не скопировать структуру явно.

Для сложных функций рекомендуется использовать проверку типов и валидацию параметров внутри тела функции, что предотвращает ошибки вычислений и повышает устойчивость скриптов.

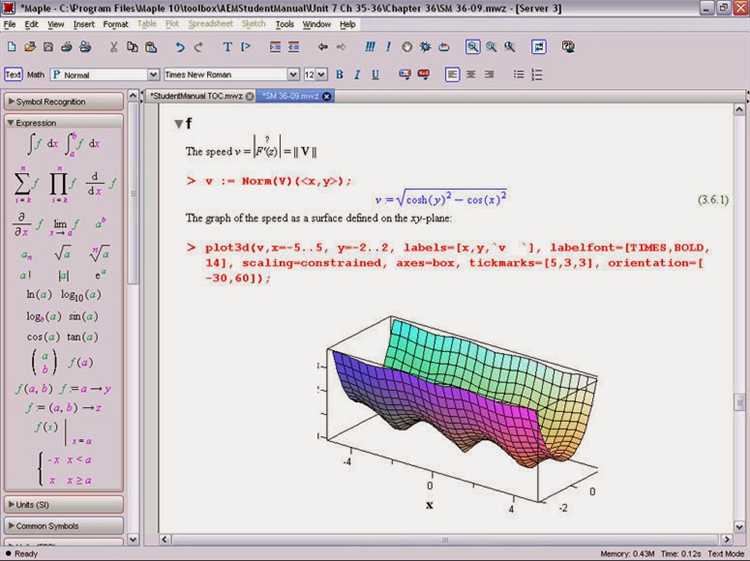
Графическое отображение функций и настройка графиков

Для построения графиков в Maple используется команда plot. Она поддерживает функции одной и нескольких переменных, а также системы уравнений. Вызов для одной переменной имеет формат: plot(f(x), x = a..b), где f(x) – выражение функции, a и b – границы интервала построения.

Для улучшения визуального восприятия графика применяются опции. Например, color задает цвет кривой, thickness – толщину линии, style – тип линии (сплошная, пунктирная и др.). Команда axes позволяет изменить вид осей, включая их расположение и наличие стрелок. Опция labels добавляет подписи к осям, а title – заголовок графика.

При построении нескольких функций используется синтаксис: plot([f(x), g(x)], x = a..b). Цвета и стили линий можно задать индивидуально с помощью списка опций, например, color = [red, blue], thickness = [2, 1]. Для более точного контроля отображения доступна опция legend, которая формирует легенду с пользовательскими подписями.

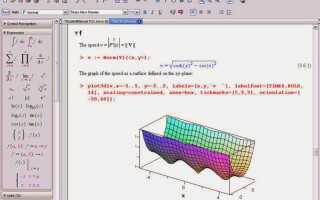
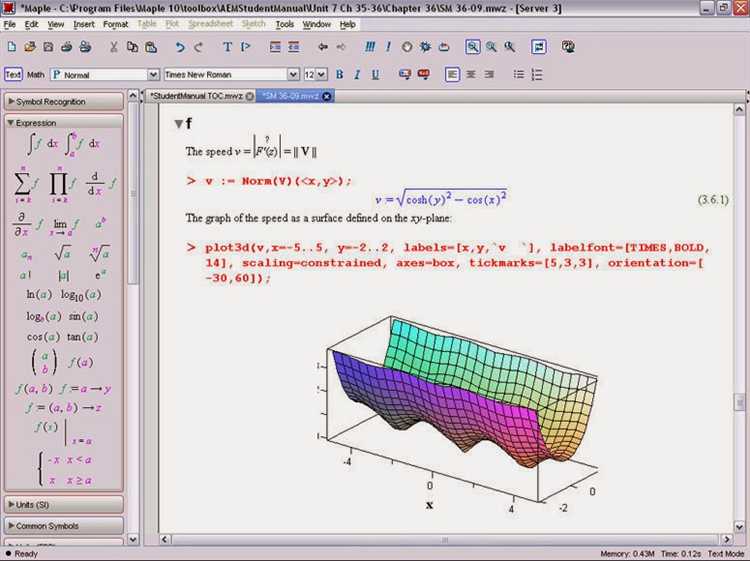
Для функций нескольких переменных применяется команда plot3d. Параметры включают области изменения переменных, например: plot3d(f(x,y), x = a..b, y = c..d). Управление видом 3D-графика достигается через orientation – угол поворота, shading – режим затенения, и axes для оформления осей.

Рекомендуется использовать опцию grid для отображения сетки, что помогает лучше оценивать расположение графика. При необходимости увеличения детализации графика задается параметр numpoints, указывающий количество вычисленных точек. Это особенно полезно для функций с резкими изменениями.

Для интерактивного анализа применяется команда interactiveplot, позволяющая масштабировать и исследовать график в режиме реального времени. Это значительно упрощает выявление особенностей функции без повторных построений.

Дифференцирование и интегрирование функций в Maple

В Maple для дифференцирования применяется команда diff. Она позволяет находить производные любой степени по заданной переменной. Для примера, чтобы вычислить первую производную функции f := x^3 + 2*x^2 - x, достаточно выполнить diff(f, x). Для получения второй производной используется diff(f, x$2).

Maple поддерживает дифференцирование по нескольким переменным, что удобно при работе с функциями нескольких аргументов. Например, diff(f(x,y), x, y) вычисляет смешанную частную производную.

Интегрирование реализуется с помощью команды int. Для вычисления неопределённого интеграла используется синтаксис int(f, x). Для определённого интеграла указывается пределы: int(f, x=a..b). Maple автоматически упрощает результаты, применяя таблицы интегралов и методы преобразования выражений.

Для сложных функций, не имеющих элементарных первообразных, Maple возвращает выражение в виде интеграла или использует численные методы через evalf(Int(f, x=a..b)).

При работе с параметрическими интегралами и производными важно явно указывать зависимости переменных, чтобы избежать неоднозначностей. Maple позволяет дифференцировать и интегрировать по параметрам, что полезно в задачах математического анализа и теории управления.

Решение уравнений с помощью функциональных выражений

В Maple функциональные выражения позволяют задавать уравнения в компактной и однозначной форме, что облегчает последующий анализ и решение. Основной инструмент – команда solve, которая принимает на вход уравнение или систему уравнений, сформулированных через функциональные выражения.

Для определения функции в Maple используется оператор :=, например, f := x -> x^2 + 3*x - 5;. Решение уравнения f(x) = 0 выполняется командой solve(f(x) = 0, x);. Такой подход позволяет легко менять функцию и сразу получать новые корни без переписывания уравнения.

При работе с функциями в уравнениях полезно использовать параметрические выражения. Например, определив g := (x,a) -> a*x^2 - 4;, можно решать уравнение для разных значений параметра a, вызывая solve(g(x, a) = 0, x);.

Если уравнение сложно аналитически, применяют численные методы через функцию fsolve, которая также принимает функциональное выражение: fsolve(f(x) = 0, x, interval);. Это особенно эффективно для поиска корней на ограниченных промежутках.

При решении систем с функциями используют списки или векторы уравнений. Например, система {f(x) = y, g(y) = x} задается как {f(x) = y, g(y) = x}, и решается через solve({f(x) = y, g(y) = x}, {x, y});.

Рекомендуется всегда проверять корректность функций, используя evalf для численных значений и subs для подстановки решений обратно в уравнения. Это гарантирует отсутствие ошибок при работе с функциональными выражениями.

Оптимизация и численный анализ функций в Maple

Maple предоставляет мощные инструменты для решения задач оптимизации и численного анализа функций, позволяя эффективно находить экстремумы и исследовать поведение сложных выражений.

1. Методы оптимизации:
   • Optimization[Minimize] и Optimization[Maximize] – функции для поиска глобальных экстремумов с поддержкой ограничений.
   • Optimization[LocalSearch] – локальный поиск экстремумов с возможностью задания начальной точки.
   • Поддержка нелинейных и ограниченных задач, включая равенства и неравенства.
2. Численный анализ:
   • fsolve – численное решение уравнений и систем, особенно эффективно при работе с нелинейными функциями.
   • evalf – вычисление приближённых значений выражений с заданной точностью.
   • Int и Sum с параметром method = numeric – численное интегрирование и суммирование.
3. Рекомендации по использованию:
   • Перед применением численных методов рекомендуется упростить функцию с помощью simplify или factor, чтобы улучшить стабильность вычислений.
   • Для задач оптимизации с ограничениями стоит явно задавать область определения, используя параметры ограничений, чтобы избежать ложных решений.
   • При работе с fsolve полезно указывать начальное приближение, особенно если уравнение имеет несколько корней.
   • Для повышения точности численных интегралов рекомендуется контролировать параметры метода через дополнительные опции, например, Digits или abserr.
4. Примеры применения:
   • Поиск минимума функции с несколькими переменными и ограничениями.
   • Нахождение численных корней сложных уравнений при помощи fsolve с заданным диапазоном поиска.
   • Численное интегрирование функций с разрывами и сложным поведением.

Использование этих инструментов в сочетании с аналитическим анализом обеспечивает точные и надёжные результаты при работе с функциями в Maple.

Вопрос-ответ:

Что такое функция в Maple и как она используется для вычислений?

Функция в Maple — это определённое выражение, которое связывает входные значения с результатами через правила вычислений. Она позволяет задавать зависимости между переменными, чтобы впоследствии можно было автоматически получать значения для разных аргументов. В Maple функции используются для упрощения расчетов, моделирования процессов и решения уравнений, где можно быстро изменять входные параметры и получать соответствующий ответ.

Какие способы создания функций в Maple существуют и чем они отличаются?

В Maple функции можно создавать несколькими способами. Например, с помощью оператора стрелки (->), который задаёт анонимную функцию, или через определение имени функции с параметрами и телом. Разница в том, что анонимная функция чаще используется для одноразовых вычислений или передачи в другие команды, а именованная функция удобна для повторного использования и более сложных программных конструкций. Кроме того, функции можно определять с помощью стандартных процедур, которые дают больше контроля над поведением.

Как в Maple работать с функциями нескольких переменных и можно ли их дифференцировать?

Функции с несколькими переменными в Maple задаются аналогично однопеременным, но с перечислением всех аргументов. Maple предоставляет встроенные инструменты для частного дифференцирования таких функций по любому из параметров. Это полезно для анализа поведения функции, нахождения экстремумов и решения задач оптимизации. Для этого применяется команда diff, которая позволяет вычислить производные любой степени по выбранной переменной.

Каковы особенности использования встроенных функций Maple по сравнению с пользовательскими?

Встроенные функции Maple написаны с высокой степенью оптимизации и охватывают широкий спектр математических операций — от арифметики до сложных трансформаций и численных методов. Они обычно работают быстрее и надежнее, чем пользовательские функции, особенно для сложных вычислений. Пользовательские функции дают гибкость, позволяя реализовывать специфические алгоритмы и логику, но требуют тщательной проверки на корректность и производительность.

Можно ли сохранять и повторно использовать функции в Maple в других сессиях или проектах?

Да, функции в Maple можно сохранять в файлы или библиотеки, чтобы использовать их позже без необходимости заново вводить код. Для этого применяют экспорт в формат, поддерживаемый Maple, или сохраняют процедуры в модули. При повторном подключении таких файлов функции становятся доступными в новом сеансе работы, что значительно облегчает повторное использование часто применяемых алгоритмов и повышает удобство работы над крупными проектами.