Система компьютерной алгебры Maple предоставляет мощный инструментарий для визуализации математических выражений. Построение графика функции здесь осуществляется с помощью встроенной процедуры plot(), которая поддерживает широкий спектр параметров – от простого отображения графиков одной переменной до сложных трёхмерных поверхностей и анимаций.
Для построения графика элементарной функции, например f(x) = sin(x), используется команда: plot(sin(x), x = -Pi..Pi). Здесь задаётся как аналитическое выражение, так и диапазон изменения переменной. Maple автоматически масштабирует оси, но при необходимости диапазоны по осям можно задавать явно с помощью параметров view.
Важной особенностью является возможность наложения нескольких графиков: plot([sin(x), cos(x)], x = 0..2*Pi) выведет обе функции на одном графике. Для кастомизации визуализации предусмотрены параметры: color, thickness, linestyle, labels и др. Например, plot(sin(x), x = 0..2*Pi, color = red, thickness = 2) увеличит толщину линии и изменит её цвет.
Maple поддерживает и трёхмерную графику. Команда plot3d(x^2 + y^2, x = -2..2, y = -2..2) строит поверхность функции двух переменных. Для более сложных задач можно использовать implicitplot и contourplot из пакета plots, предварительно вызвав его через with(plots):.
Понимание синтаксиса и параметров визуализации в Maple критично при работе с прикладными и исследовательскими задачами. Гибкость и точность построения графиков позволяют использовать Maple не только для демонстрации, но и для анализа поведения функций в различных условиях.
Как построить график элементарной функции с помощью команды plot
В Maple команда plot используется для построения графиков действительных функций одной переменной. Синтаксис следующий:
plot(f(x), x=a..b);Где f(x) – функция, x=a..b – диапазон по оси x.
- Для построения графика синуса на отрезке от 0 до 2π:
plot(sin(x), x=0..2*Pi); - Чтобы изменить число точек построения (например, 500):
plot(sin(x), x=0..2*Pi, numpoints=500); - Для задания цветовой схемы:
plot(x^2, x=-5..5, color=blue); - Ограничение диапазона по оси y:
plot(exp(x), x=-2..2, y=0..10); - График нескольких функций на одном поле:
plot([sin(x), cos(x)], x=0..2*Pi); - Использование имени функции:
f := x -> ln(x): plot(f(x), x=1..10);
Рекомендуется использовать numpoints для повышения точности отрисовки при резких колебаниях функции. Для наглядности графика можно применять параметры thickness (толщина линии), style (например, line, point) и legend при построении нескольких функций:
plot([x, x^2], x=-2..2, legend=["x", "x^2"], thickness=2);Задание диапазона переменных при построении графика
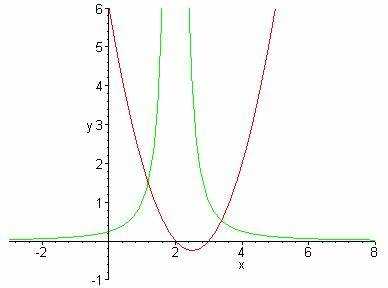
В Maple при построении графиков функций необходимо явно указывать диапазон значений переменной, чтобы контролировать область отображения. Это делается непосредственно в команде plot.
Формат задания диапазона:
plot(f(x), x = a..b);
f(x)– функция, график которой строится;x = a..b– диапазон переменной x от a до b включительно.
Для построения графика функции sin(x) от 0 до 2π:
plot(sin(x), x = 0..2*Pi);
Если диапазон не задан, Maple по умолчанию выбирает его самостоятельно, что может привести к частичному или некорректному отображению графика.
При работе с несколькими переменными в функции необходимо указывать диапазоны каждой из них:
plot3d(sin(x)*cos(y), x = -Pi..Pi, y = -Pi..Pi);
- Для двумерных графиков используется
plot, диапазон задаётся для одной переменной. - Для трёхмерных –
plot3d, диапазоны задаются для обеих переменных.
Рекомендуется всегда задавать диапазон явно, особенно при исследовании поведения функции на конкретном участке или при наличии особенностей (разрывов, асимптот).
Для построения графика на симметричном интервале:
plot(1/x, x = -5..5);
Однако, в этом примере при x = 0 возникает разрыв. Чтобы избежать ошибок, следует исключить нулевое значение:
plot(1/x, x = -5..-0.1 union 0.1..5);
Диапазон можно задавать с высокой точностью, используя дроби или вещественные числа:
plot(exp(-x^2), x = -1.5..1.5);
Для функций, определённых на ограниченном интервале, корректный диапазон позволяет избежать построения вне области определения:
plot(ln(x), x = 0.01..5);
Использование адекватных диапазонов делает график наглядным, избегая искажений и неопределённых значений.
Построение нескольких функций на одном графике
Для отображения нескольких функций на одном графике в Maple используйте команду plot с передачей списка выражений. Пример:
plot([sin(x), cos(x), x/2], x = -Pi .. Pi)
Каждая функция из списка будет отображена с уникальным цветом. Чтобы задать индивидуальные параметры отображения, используйте список списков:
plot([[sin(x), color = red, linestyle = dash], [cos(x), color = blue, thickness = 2], [x/2, color = green]], x = -Pi .. Pi)
Если требуется подписать графики, примените параметр legend:
plot([[sin(x), legend = «sin(x)»], [cos(x), legend = «cos(x)»], [x/2, legend = «x/2»]], x = -Pi .. Pi)
Для лучшего восприятия используйте параметры axes = boxed и gridlines = true. Это добавит рамку и сетку:
plot([sin(x), cos(x)], x = -Pi .. Pi, axes = boxed, gridlines = true)
Если необходимо изменить порядок наложения графиков, расположите их в нужной последовательности в списке. Для сложных композиций предпочтительнее использовать display из пакета plots:
with(plots):
p1 := plot(sin(x), x = 0 .. 2*Pi, color = red):
p2 := plot(cos(x), x = 0 .. 2*Pi, color = blue):
display([p1, p2])
Комбинируя параметры и функции, добивайтесь наглядного и точного представления данных на едином графике.
Настройка цвета, стиля линий и толщины графика
В Maple параметры внешнего вида графика задаются непосредственно в команде plot с использованием опций color, linestyle и thickness. Эти параметры позволяют точно управлять визуализацией графика функции.
Цвет линии указывается через параметр color. Допустимы как текстовые значения (например, "red", "blue"), так и RGB-формат с использованием записи COLOR(R, G, B), где каждое значение находится в диапазоне от 0 до 1. Пример: plot(sin(x), x = 0..2*Pi, color = COLOR(0.2, 0.6, 0.8)).
Стиль линии регулируется параметром linestyle. Доступные значения:
1– сплошная линия (по умолчанию)2– пунктир3– штрих-пунктир4– точечная5– длинный штрих-пунктир
Пример использования: plot(cos(x), x = 0..2*Pi, linestyle = 3).
Толщина линии задаётся с помощью параметра thickness, где значение – это целое число от 0 до 5. При этом 0 соответствует самой тонкой линии, а 5 – самой толстой. Пример: plot(exp(-x), x = 0..5, thickness = 4).
Комбинация всех параметров:
plot(tan(x), x = -Pi/2..Pi/2, color = "green", linestyle = 2, thickness = 3)Такая запись создаёт график тангенса с зелёной пунктирной линией средней толщины.
Использование параметров отображения: сетка, подписи, масштаб
Для повышения наглядности графика в Maple следует управлять параметрами визуализации. Используйте опцию gridlines=true в команде plot, чтобы отобразить сетку. Это помогает точно интерпретировать координаты точек. Дополнительно можно задать формат gridlines=[xшаг, yшаг], например gridlines=[0.5, 1].
Для добавления подписей к осям применяются параметры labels=["ось X", "ось Y"]. Чтобы указать шрифт и размер подписей, используйте вложенные опции labelfont=["Arial", 12]. Надпись над графиком задаётся через title="Название графика", её стиль можно задать через titlefont=["Times", 14].
Для изменения масштаба осей применяется опция scaling. Значение scaling=constrained сохраняет пропорции по осям, особенно полезно при построении кругов или симметричных объектов. Значение scaling=unconstrained позволяет использовать автоматическую подгонку диапазонов, что удобно для графиков с сильно отличающимися диапазонами по осям.
Явное задание диапазонов осей производится через plot(f, x=a..b, y=c..d). Это исключает автоматическое обрезание графика и гарантирует отображение всех интересующих областей функции.
Для сложных графиков используйте axes=boxed или axes=framed для более точной ориентации в координатной системе. Опция tickmarks=[xметки, yметки] позволяет задать конкретные значения делений осей, например tickmarks=[[0, π/2, π], [0, 1]].
Построение графика параметрически заданной функции
В Maple параметрически заданную функцию задают в виде системы уравнений с параметром t. Для построения графика используют команду plot с набором пар (x(t), y(t)) и интервалом изменения параметра.
Пример синтаксиса для кривой:
plot([x(t), y(t), t = a..b]);
Где x(t) и y(t) – функции параметра t, a и b – границы интервала параметра. Интервал задаёт область построения, важно выбирать его так, чтобы график полностью отображал кривую.
Для сложных функций или нескольких кривых используют список или массив:
plot({[x1(t), y1(t), t = a..b], [x2(t), y2(t), t = c..d]});
В случае с комплексными параметрическими уравнениями рекомендуется предварительно проверить область определения и устранить особенности, такие как разрывы или неопределённости, чтобы избежать артефактов на графике.
Для настройки внешнего вида графика применяют дополнительные опции:
color – цвет линии,
thickness – толщина,
legend – подписи кривых. Например:
plot([x(t), y(t), t = 0..2*Pi], color=red, thickness=2);
Параметрические графики удобно использовать для визуализации кривых Безье, спиралей, эллипсов и траекторий движения, где традиционная функция y = f(x) неприменима.
Сохранение графика в файл и экспорт в графические форматы
plotsetup('png', plotoutput = 'имя_файла.png', plotoptions = ['-width=800', '-height=600']):
plot(sin(x), x = 0..2*Pi);
Поддерживаемые форматы: PNG, JPEG, BMP, TIFF, EPS, PDF. Форматы векторной графики (EPS, PDF) рекомендуются для последующей печати и публикаций, так как обеспечивают масштабируемость без потери качества.
При использовании форматов растровой графики (PNG, JPEG) важно учитывать разрешение, которое задаётся через параметры -width и -height. Рекомендуется устанавливать ширину от 600 до 1200 пикселей для детализированных изображений.
Для экспорта нескольких графиков в один файл поддерживается создание многостраничных PDF-документов через последовательные вызовы функций с включённым plotsetup('pdf', plotoutput='имя_файла.pdf').
Автоматический экспорт возможен при использовании опции plotoutput в plotsetup, что позволяет избежать ручного сохранения через интерфейс.
Если требуется экспорт только части графика, можно предварительно настроить области отображения с помощью параметров view в функции plot.
Для пакетной обработки рекомендуют оформлять сохранение графиков в процедуры, где задаются параметры формата, размера и имени файла.
Вопрос-ответ:
Как построить график функции с помощью Maple?
В Maple для построения графика функции используют команду plot(). Внутри скобок указывают выражение функции и диапазон значений переменной. Например, plot(sin(x), x=0..2*Pi) построит график синуса от 0 до 2π. Можно также задать дополнительные параметры, такие как цвет линии или толщина, чтобы улучшить внешний вид графика.
Можно ли построить график функции нескольких переменных в Maple?
Да, Maple позволяет строить графики функций двух переменных. Для этого используют команду plot3d(). Например, plot3d(x^2 + y^2, x=-2..2, y=-2..2) создаст трехмерный график функции z = x² + y² в заданном диапазоне по x и y. Также доступны параметры для настройки цвета, освещения и угла обзора, чтобы сделать визуализацию более информативной.
Как настроить масштаб осей при построении графика функции в Maple?
Чтобы изменить масштаб осей, можно использовать опцию axes, которая позволяет отображать или скрывать оси, а также задать пределы по каждой оси отдельно. Например, plot(f(x), x=a..b, y=c..d, axes=boxed) построит график с определёнными ограничениями по оси y. Если необходимо более тонкое управление, можно применить опцию view=[xmin..xmax, ymin..ymax], чтобы задать область отображения графика.
Как построить график функции с несколькими ветвями или разрывами в Maple?
Если функция имеет несколько ветвей или точки разрыва, можно построить графики отдельных частей по отдельности и объединить их с помощью команды display() из пакета plots. Например, сначала создают графики для каждого участка, а затем объединяют их, чтобы получить полный рисунок функции с учётом особенностей. Такой подход помогает избежать искажений в местах разрывов и отображать структуру функции корректно.
Можно ли сохранять графики из Maple в виде изображений для дальнейшего использования?
Да, Maple позволяет сохранять построенные графики в различных форматах, например PNG, JPEG, PDF и других. Для этого после построения графика можно использовать меню сохранения или команды exportplot(). При экспорте можно задать разрешение и размеры изображения, что удобно для подготовки материалов для отчетов или презентаций.
Как построить график функции с несколькими переменными в Maple?
Для построения графика функции с несколькими переменными в Maple можно использовать команду plot3d. Например, чтобы изобразить поверхность, заданную функцией z = x^2 + y^2, нужно выполнить plot3d(x^2 + y^2, x = -2..2, y = -2..2). Эта команда создаст трехмерное изображение функции в заданных пределах для x и y. Можно настроить внешний вид графика с помощью дополнительных опций, таких как цвет, угол обзора и качество прорисовки.
Можно ли в Maple построить график функции и сразу получить ее аналитическое выражение с помощью графического интерфейса?
Maple позволяет создавать графики функций как с помощью команд в текстовом окне, так и через графический интерфейс. Однако автоматически получать аналитическое выражение функции на основе графика система не умеет. Для построения графика необходимо либо задать формулу функции вручную, либо импортировать ее из вычислений. Графический интерфейс облегчает ввод функции и настройку отображения, но не заменяет необходимость определения формулы. Если требуется обратное получение формулы по графику, это потребует применения методов аппроксимации и анализа данных, которые в Maple реализованы отдельно.