Как обратиться к элементу матрицы в matlab

В Matlab матрицы являются фундаментальной структурой данных, и умение эффективно обращаться к их элементам критично для оптимизации кода и корректного выполнения вычислений. Индексация в Matlab основана на позициях элементов, начиная с 1, что отличает его от многих языков программирования с нулевой индексацией.

Доступ к отдельным элементам реализуется через круглые скобки и указание строкового и столбцового индексов: A(i,j). Для одномерных векторов индекс указывается единственным числом. Важно помнить, что выход за пределы размерности приводит к ошибке, поэтому индексы должны строго соответствовать размерам матрицы.

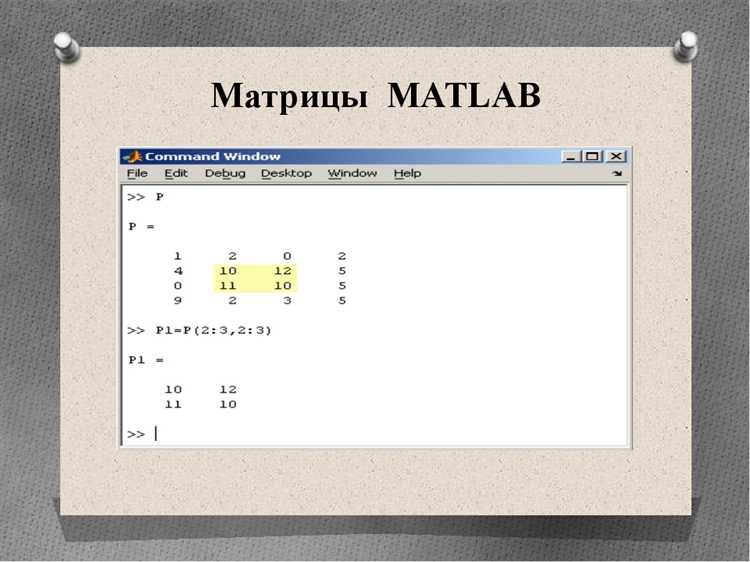
Обращение к подматрицам выполняется с помощью диапазонов индексов, например, A(2:4, 1:3) возвращает блок из строк 2-4 и столбцов 1-3. Можно использовать двоеточие : для выбора всех элементов по одному измерению, что упрощает операции над строками или столбцами.

Для динамического изменения размеров и содержимого матрицы индексами задают позицию вставки новых элементов. При этом Matlab автоматически расширяет матрицу, заполняя новые позиции нулями. При работе с логическими индексами или масками можно выбирать элементы, удовлетворяющие условиям, без явного перечисления индексов.

Синтаксис индексации отдельных элементов матрицы

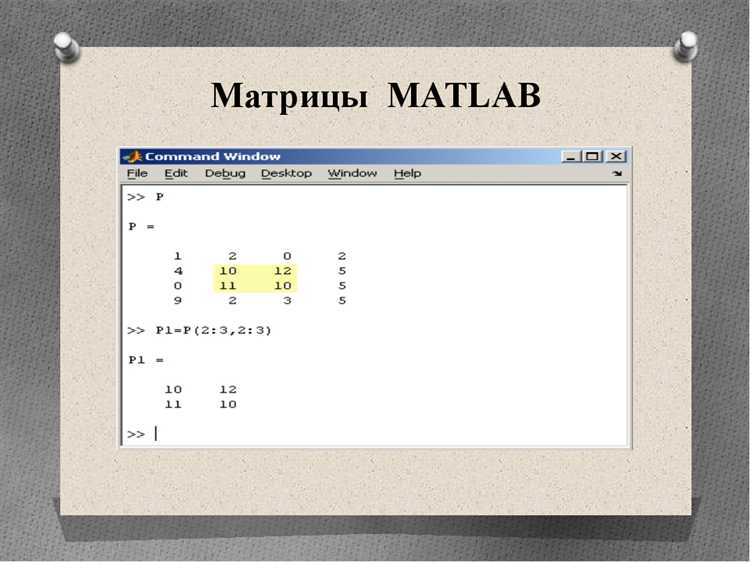
В MATLAB для обращения к конкретному элементу матрицы используется конструкция с круглыми скобками и двумя индексами: А(i, j), где i – номер строки, j – номер столбца. Индексация начинается с 1, а не с 0, что важно учитывать при работе с массивами.

Для выбора одного элемента необходимо указать точные значения индексов. Например, A(3,2) вернёт элемент из третьей строки второго столбца матрицы A. При выходе за границы массива MATLAB выдаст ошибку.

Индексы могут быть переменными или выражениями, например A(i, j+1), что даёт гибкость при программировании и циклах.

Можно использовать линейную индексацию, задавая один индекс: A(k). Здесь элементы считаются построчно. Например, для матрицы размером 3×3 элемент A(5) соответствует элементу A(2,2).

Для выбора нескольких отдельных элементов используют векторы индексов: A([1 3 5]) – выбор элементов с линейными индексами 1, 3 и 5. Аналогично для двумерной индексации: A([1 2], [3 4]) вернёт подматрицу из строк 1 и 2 и столбцов 3 и 4.

Для замены элемента или группы элементов достаточно присвоить новое значение по указанным индексам: A(2,1) = 10; или A([1 3], 2) = [5; 7];.

Извлечение строк и столбцов из матрицы

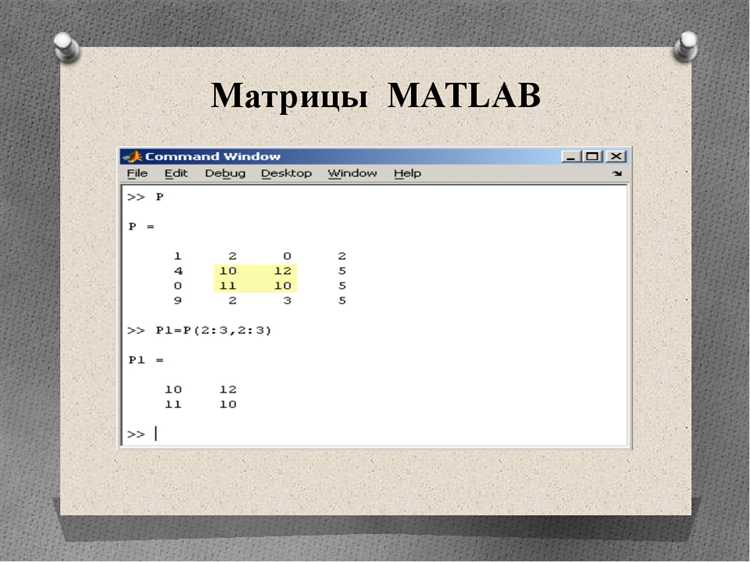
В Matlab для доступа к конкретным строкам и столбцам матрицы применяют индексирование с помощью двоеточия и векторов индексов.

• Извлечение строки: для получения i-й строки используется синтаксис A(i, :), где A – матрица, i – номер строки.
• Извлечение столбца: для выбора j-го столбца применяется A(:, j).

Для извлечения нескольких строк или столбцов используют векторы индексов:

• A([i1 i2 i3], :) – строки с номерами i1, i2, i3.
• A(:, [j1 j2 j3]) – столбцы с номерами j1, j2, j3.

Двоеточие можно комбинировать с шагом для выбора диапазона с пропусками:

• A(1:2:5, :) – строки с 1 по 5 через одну (1, 3, 5).
• A(:, 2:4) – столбцы со 2-го по 4-й подряд.

Чтобы получить непрерывный блок матрицы, указывают диапазоны по строкам и столбцам одновременно:

• A(2:4, 3:5) – подматрица из строк 2–4 и столбцов 3–5.

При работе с векторами индексов важно соблюдать диапазон: индексы должны быть целыми положительными числами и не выходить за размеры матрицы, иначе возникает ошибка.

Для динамического извлечения строк или столбцов используют логические индексы:

• A(logicalVector, :) – строки, где logicalVector равен true.
• A(:, logicalVector) – столбцы по аналогии.

Это удобно, например, для выбора строк по условию.

Использование логической индексации для выбора элементов

Логическая индексация в MATLAB позволяет выбирать элементы матрицы, удовлетворяющие определённому условию, без необходимости перебора в цикле. Для этого создаётся логическая матрица того же размера, где элементы принимают значение true (1) или false (0) в зависимости от проверки условия.

Пример: если A – матрица, выражение A > 5 вернёт логическую матрицу, где true соответствует элементам больше 5. Для получения самих значений используется индексация: A(A > 5) вернёт вектор всех элементов матрицы A, превышающих 5.

Логическая индексация работает с любыми условиями, включая сложные комбинации с использованием операторов & (логическое И), | (логическое ИЛИ), ~ (отрицание). Например, A(A > 0 && A <= 10) вернёт элементы, лежащие в диапазоне от 1 до 10 включительно.

Для замены элементов, удовлетворяющих условию, используют присваивание: A(A < 0) = 0 заменит все отрицательные значения в матрице на нули. Это позволяет эффективно фильтровать и модифицировать данные.

Важно помнить, что результат логической индексации – одномерный вектор, состоящий из выбранных элементов по столбцам матрицы. Для сохранения размерности или выбора элементов по строкам и столбцам используют дополнительную обработку или функции, такие как find.

Логическая индексация значительно ускоряет операции с большими массивами, сокращая код и повышая читаемость программ на MATLAB.

Обращение к элементам с помощью линейной индексации

В MATLAB матрицы хранятся в памяти построчно, что позволяет обращаться к элементам не только по двумерным индексам, но и по единому линейному индексу. Линейная индексация используется для последовательного доступа ко всем элементам матрицы без указания строк и столбцов.

Особенности и правила работы с линейной индексацией:

• Индексация начинается с 1 и продолжается до количества элементов (numel) в матрице.
• Элемент с линейным индексом k соответствует позиции k-го элемента при чтении матрицы построчно.
• Для матрицы A размера m × n линейный индекс k можно преобразовать в пару (i, j) с помощью:

1. i = mod(k-1, m) + 1
2. j = floor((k-1)/m) + 1

• Обратное преобразование от (i, j) к k выполняется как k = i + (j-1)*m.
• При обращении через линейный индекс можно изменять или извлекать элементы, например, A(k) или A([k1, k2, k3]).
• Линейная индексация эффективна для обхода всей матрицы или для работы с подмножествами элементов без вычисления двумерных индексов.
• Важно учитывать, что для векторов (строковых или столбцовых) линейная и обычная индексация совпадают.

Пример использования линейной индексации:

1. Создание матрицы: A = reshape(1:12, 3, 4);
2. Обращение к элементу с линейным индексом 5: A(5) возвращает элемент из 2-й строки и 2-го столбца.
3. Изменение значений: A([2, 7, 10]) = 0; присваивает нули выбранным элементам.

Изменение значений элементов по индексам

В Matlab для изменения значения конкретного элемента матрицы используют индексацию по строке и столбцу: A(i,j) = новое_значение;. Здесь i и j – номера строки и столбца соответственно. Индексы должны быть целыми положительными числами и находиться в пределах размеров матрицы.

Для изменения нескольких элементов одновременно применяют векторные или логические индексы. Например, A([2,4],3) = [10; 20]; изменит элементы во 2-й и 4-й строках третьего столбца. При использовании логических массивов размер индекса должен совпадать с размером матрицы или с выбранным измерением.

Обращение к элементам по линейному индексу возможно через одноколоночный формат: A(k) = значение;, где k – позиция элемента при чтении матрицы по столбцам. Для изменения нескольких элементов задайте вектор индексов: A([3 7 10]) = [5 8 2];.

При присваивании нового значения важно, чтобы размер массива справа совпадал с количеством изменяемых элементов, иначе возникнет ошибка несоответствия размерностей. Изменение элементов в пределах существующего размера матрицы не вызывает расширения, добавление вне диапазона индексов автоматически увеличит размер матрицы, заполнив промежутки нулями.

Работа с подматрицами и блоками элементов

Для выделения подматрицы в Matlab используется синтаксис с указанием диапазона индексов: A(i:j, k:l). Здесь i:j – строки, k:l – столбцы. Например, A(2:4, 3:5) возвращает блок из строк 2–4 и столбцов 3–5 матрицы A. Диапазоны могут задаваться в любом порядке, включая обратный, например 5:-1:3, что обращает порядок элементов.

Для работы с блоками важно помнить, что индексы в Matlab начинаются с 1. Извлечённая подматрица сохраняет структуру, что позволяет применять к ней функции и операции, аналогично полной матрице.

Чтобы заменить блок элементов, достаточно присвоить значение по тем же индексам, например: A(1:3, 2:4) = B, где B – матрица с размером, совпадающим с выделяемым блоком.

Выделение подматриц с использованием логических индексов позволяет обращаться к элементам по условию. Например, A(A > 10) возвращает все элементы матрицы A, превышающие 10, но в виде вектора. Для сохранения исходной размерности лучше использовать маскирование с присваиванием NaN или нулей.

Для сложных структур подматриц используют функции reshape, permute и mat2cell, позволяющие менять размер и форму блоков без потери данных. Например, reshape(A(1:12), [3,4]) преобразует выбранный участок в матрицу 3×4.

При циклическом обходе подматриц для обработки блоков рекомендуется использовать вложенные циклы с чётко заданными границами, либо функцию blockproc (Image Processing Toolbox) для автоматизации обработки блоков фиксированного размера.

Следует учитывать, что операции с большими подматрицами требуют оптимизации по памяти. Используйте присваивания по ссылке, избегайте излишнего копирования данных, а при необходимости используйте sparse-матрицы.

Обращение к элементам многомерных массивов

Многомерные массивы в MATLAB индексируются через запятую, где каждый индекс соответствует размерности массива. Для массива A с размерностью n доступ к элементу осуществляется с помощью записи A(i1, i2, …, in), где i1, i2, …, in – целочисленные индексы по соответствующим осям.

Для обращения к подмассивам используется диапазон индексов через двоеточие. Например, A(2:4, 1:3, 5) выберет элементы с 2 по 4 по первой размерности, с 1 по 3 по второй и фиксированное значение 5 по третьей.

Если нужно получить срез по конкретной размерности, оставляя остальные полностью, применяется двоеточие для всех остальных индексов, например, A(:, :, 3) – извлечёт весь двумерный срез третьей плоскости.

Индексы в MATLAB всегда начинаются с 1, обращение с нулевыми или отрицательными индексами вызывает ошибку.

Для динамического обращения к элементам многомерных массивов можно использовать функцию subsref или cell array индексацию, если структура нестандартная. Однако для обычных массивов предпочтительнее использовать стандартный синтаксис с запятыми.

При работе с многомерными массивами важно учитывать, что MATLAB хранит данные в памяти по столбцовому принципу (column-major order). Это влияет на скорость выполнения операций с частыми доступами к элементам, поэтому последовательный проход по первой размерности эффективнее.

Вопрос-ответ:

Как в Matlab обратиться к элементу матрицы по строке и столбцу?

Для получения значения отдельного элемента матрицы нужно указать индекс строки и столбца в круглых скобках через запятую. Например, A(2,3) вернёт элемент, находящийся во второй строке и третьем столбце матрицы A.

Можно ли в Matlab получить сразу несколько элементов из матрицы с помощью диапазона индексов?

Да, для обращения к группе элементов используют двоеточие. Например, выражение A(1:3, 2:4) выберет элементы из строк с 1 по 3 и столбцов с 2 по 4 включительно. Таким образом можно извлечь подматрицу.

Как в Matlab обратиться к элементам всей строки или столбца матрицы?

Чтобы получить всю строку, например первую, нужно указать её номер и двоеточие для столбцов: A(1, :). Аналогично, чтобы взять весь столбец, указывают двоеточие для строк и номер столбца, например A(:, 2) — это второй столбец матрицы.

Можно ли менять значения отдельных элементов матрицы по индексам в Matlab?

Да, Matlab позволяет изменять значения конкретных элементов, обращаясь к ним по индексам и присваивая новое значение. Например, команда A(3,4) = 10 заменит элемент из третьей строки и четвёртого столбца матрицы A на 10.