В Mathcad вычисление аргумента комплексного числа выполняется с помощью встроенной функции arg(), которая возвращает угол в радианах между положительным направлением действительной оси и вектором комплексного числа на комплексной плоскости.
Для корректного результата важно передавать функции именно комплексное число в формате a + b·i, где a – действительная часть, b – мнимая. При этом Mathcad автоматически обрабатывает знаки и положения чисел в четвертях, обеспечивая правильное значение аргумента.
В случае комплексных выражений, содержащих переменные, важно убедиться, что переменные имеют числовые значения до вызова arg(), иначе Mathcad не сможет вычислить аргумент.
Формат записи комплексных чисел в Mathcad
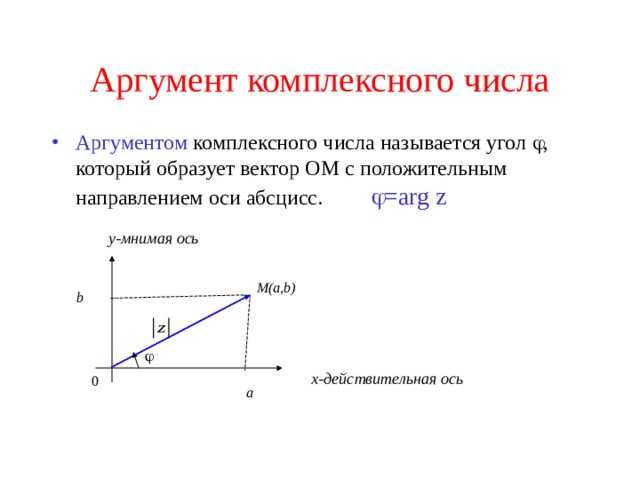
В Mathcad комплексные числа задаются в виде суммы действительной и мнимой частей с использованием символа i или j для обозначения мнимой единицы. Правила записи:
- Действительная часть и мнимая разделяются знаком
+или-, например:3 + 4iили5 - 2j. - Мнимая часть должна содержать коэффициент перед
iилиj. Записьiэквивалентна1i. - Для записи комплексных чисел в виде векторного массива используется формат
[a, b], гдеa– действительная, аb– мнимая часть. - Функция
rect(z)преобразует комплексное числоzк формеa + bi, гдеaиb– действительная и мнимая части соответственно. - Для задания комплексных чисел в полярной форме используется функция
polar(r, θ), гдеr– модуль, аθ– аргумент в радианах.
Важно избегать пробелов между числом и мнимой единицей: 3 + 4i корректно, а 3 + 4 i вызовет ошибку.
Mathcad распознает комплексные выражения и автоматически определяет их тип, что позволяет применять функции вычисления модуля и аргумента без дополнительных преобразований.
Функция Arg() для вычисления аргумента

В Mathcad функция Arg() служит для определения аргумента комплексного числа, то есть угла в радианах между положительным направлением оси действительных чисел и вектором, соответствующим комплексному числу на комплексной плоскости. Синтаксис функции прост: Arg(z), где z – комплексное число.
Аргумент возвращается в диапазоне от -π до π, что соответствует стандартному определению в тригонометрической форме комплексных чисел. При работе с числом вида z = x + yi, функция вычисляет аргумент по формуле atan2(y, x), обеспечивая корректное определение квадранта.
В Mathcad функция Arg() удобна для аналитических вычислений и построения графиков, так как интегрируется с другими встроенными функциями комплексного анализа. При необходимости использовать аргумент в градусах, рекомендуется дополнительно применять преобразование: Arg(z) * 180/π.
Особое внимание следует уделять случаям, когда x=0 и y=0, поскольку аргумент в этой точке не определён. В Mathcad в таком случае функция возвращает 0, что следует учитывать при анализе результатов.
Для более комплексных операций с комплексными числами рекомендуется использовать вместе с Arg() функцию abs() для вычисления модуля и строить комплексные выражения в полярной форме.
Применение Arg() к числам с положительной и отрицательной действительной частью
Функция Arg() в Mathcad вычисляет аргумент комплексного числа, определяемый как угол между положительным направлением оси действительных чисел и вектором, представляющим комплексное число на комплексной плоскости.
Для чисел с положительной действительной частью аргумент находится в диапазоне от -π/2 до π/2. Если число имеет положительную действительную часть и положительную мнимую, Arg() возвращает значение в первом квадранте (от 0 до π/2). При отрицательной мнимой части аргумент будет отрицательным, но ограничен -π/2.
Для чисел с отрицательной действительной частью результат Arg() смещается на π или -π. При положительной мнимой части аргумент лежит в интервале (π/2, π), при отрицательной – в диапазоне (-π, -π/2). Это важно учитывать при анализе, так как простое вычисление atan(Im/Re) в Mathcad без дополнительной обработки приводит к неправильному знаку аргумента для чисел с отрицательной действительной частью.
В Mathcad рекомендуется использовать функцию Arg() напрямую, так как она корректно учитывает знаки и обеспечивает вычисление в нужном квадранте. Если же необходимо вручную вычислять аргумент через arctan, следует реализовывать проверку знаков действительной и мнимой частей и добавлять π или -π при отрицательной действительной части для корректировки результата.
Для комплексных чисел с действительной частью, равной нулю, Arg() возвращает π/2 при положительной мнимой и -π/2 при отрицательной, что соответствует расположению на оси мнимых чисел. Такое поведение важно учитывать при обработке данных, особенно если возможны граничные случаи.
Практическое применение Arg() в Mathcad требует внимательного отношения к знакам компонентов комплексного числа и понимания распределения аргумента по квадрантам, что исключает ошибки при моделировании и расчетах, связанных с комплексной арифметикой.
Работа с комплексными числами в тригонометрической форме

Комплексное число в тригонометрической форме задаётся как \( z = r(\cos \varphi + i \sin \varphi) \), где \( r \) – модуль, а \( \varphi \) – аргумент. В Mathcad перевод числа в эту форму требует вычисления модуля через функцию abs(z) и аргумента через arg(z), что позволяет затем использовать тригонометрические операции напрямую.
При умножении комплексных чисел в тригонометрической форме достаточно перемножить модули и сложить аргументы:
\( z_1 \cdot z_2 = r_1 r_2 [\cos(\varphi_1 + \varphi_2) + i \sin(\varphi_1 + \varphi_2)] \). В Mathcad для аргументов применяется функция arg(), при этом важно соблюдать диапазон значений аргумента, часто возвращаемого в интервале \(-\pi, \pi\).
Возведение в степень удобно реализуется через формулу Моавра:
\( z^n = r^n [\cos(n\varphi) + i \sin(n\varphi)] \). В Mathcad модуль возводится в степень через оператор ^, а аргумент умножается на степень.
Обратная операция – извлечение корня – требует разложения аргумента на равные части:
\( \sqrt[n]{z} = \sqrt[n]{r} \left[ \cos\left(\frac{\varphi + 2k\pi}{n}\right) + i \sin\left(\frac{\varphi + 2k\pi}{n}\right) \right], \quad k=0,1,…,n-1 \). Для корректного вычисления всех корней в Mathcad следует использовать циклы или векторные операции для параметра \( k \).
При работе с аргументом в Mathcad стоит учитывать, что функция arg() возвращает значение в радианах. Для преобразования в градусы используйте умножение на \( \frac{180}{\pi} \). Для удобства вычислений с углами рекомендуется создавать вспомогательные переменные для радиан и градусов.
Тригонометрическая форма комплексного числа оптимальна для операций, где важны угол и длина вектора, что облегчает анализ и визуализацию в полярной системе координат, доступной в Mathcad через встроенные функции и графические модули.
Как обрабатывать случаи с аргументом равным нулю или π

В Mathcad вычисление аргумента комплексного числа, расположенного на вещественной оси, требует особого внимания. Если комплексное число имеет вид z = x + 0i, где x > 0, аргумент равен 0. При x < 0 аргумент равен π (или −π, в зависимости от используемой функции).
Функция arg(z) в Mathcad возвращает результат в диапазоне от −π до π. Для точного определения угла при y=0 нужно контролировать знак действительной части:
1. Если Im(z) = 0 и Re(z) > 0, то arg(z) = 0.
2. Если Im(z) = 0 и Re(z) < 0, то arg(z) = π.
3. Если Re(z) = 0 и Im(z) = 0, аргумент не определён, и необходимо предусмотреть обработку исключения или возвращать значение по умолчанию.
Рекомендуется реализовать дополнительную проверку перед вызовом arg(z), чтобы исключить влияние погрешностей округления и избежать ложных значений угла. Например, можно задать пороговое значение для Im(z), ниже которого считать его нулём.
Использование функции atan2(Im(z), Re(z)) в Mathcad обеспечивает корректное вычисление аргумента с учётом знаков компонентов, однако при Im(z) = 0 и отрицательном Re(z) результат будет равен ±π, что требует единообразной интерпретации.
Использование встроенных инструментов Mathcad для визуализации аргумента
Mathcad предоставляет набор функций для построения комплексных чисел на комплексной плоскости, что позволяет наглядно определить аргумент. Для визуализации следует использовать графический инструмент «График XY», где по оси X откладывается действительная часть, а по оси Y – мнимая часть комплексного числа.
Для построения в Mathcad введите комплексное число в формате z := x + i*y, где x и y – числовые значения. Далее создайте вектор точек z_vec := [Re(z), Im(z)]. Постройте график с помощью функции plot(z_vec) или через интерфейс «График XY», указав соответствующие векторы по осям.
Для выделения аргумента используйте встроенную функцию arg(z), которая возвращает угол в радианах. Значение можно отобразить на графике с помощью текстового поля, либо построить луч от начала координат до точки (Re(z), Im(z)). Для этого создайте второй вектор, соединяющий начало с точкой, и отобразите его на том же графике.
Для более детальной визуализации рекомендуется использовать функцию «Полярный график». В Mathcad она доступна через преобразование координат: задайте радиус r := abs(z) и угол θ := arg(z). Затем постройте полярный график, где радиус и угол отображают точку в полярных координатах, наглядно демонстрируя аргумент.
Автоматизация визуализации возможна через создание динамических переменных с помощью слайдеров для x и y. При изменении параметров положение точки и значение аргумента обновляются мгновенно, что упрощает анализ и понимание зависимости аргумента от координат.
Обработка ошибок и исключительных значений при вычислении аргумента

В Mathcad вычисление аргумента комплексного числа реализуется функцией arg(z), где z = x + yi. При этом возможны специфические ситуации, требующие отдельной обработки для предотвращения некорректных результатов и ошибок.
- Пограничные значения на вещественной оси: При
Im(z) = 0иRe(z) > 0аргумент равен 0, приRe(z) < 0– ±π. Mathcad корректно вычисляет эти значения, но в задачах, где важен знак угла, стоит явно контролировать вычисление, особенно при приближении к нулю по мнимой части. - Погрешности округления: Для комплексных чисел с очень малыми значениями мнимой или вещественной части могут возникать ошибки из-за ограниченной точности. Рекомендуется использовать функцию
roundс заданной точностью перед вычислением аргумента, чтобы избежать скачков и непредвиденных результатов. - Многочленные ветвления аргумента: В Mathcad значение аргумента возвращается в пределах (-π, π]. Если необходимо получить аргумент в другом интервале (например, [0, 2π)), реализуйте нормализацию вручную, добавляя условие
if arg(z) < 0 then arg(z) + 2π else arg(z). - Обработка ошибок функций ввода: При вычислении аргумента для результатов, полученных из внешних источников или пользовательского ввода, проверяйте тип и формат данных. Используйте встроенные функции Mathcad для валидации чисел, чтобы избежать ошибок преобразования.
Реализация комплексных вычислений в Mathcad требует системного подхода к обработке частных случаев и исключений, особенно при автоматизации расчетов и построении инженерных моделей. Предварительные проверки значений и явная нормализация аргумента повышают устойчивость и точность вычислений.
Примеры расчётов аргумента комплексных чисел в реальных задачах
В электродинамике для анализа фазовых сдвигов напряжения и тока используются комплексные сопротивления. Например, для сопротивления Z = 3 + 4i, аргумент вычисляется как arctg(4/3) ≈ 53,13°. В Mathcad достаточно задать Z := 3 + 4i и применить функцию arg(Z) для получения точного значения.
В задачах управления колебательными системами часто встречаются комплексные корни характеристического уравнения. Для корня s = -1 + 2i аргумент равен arctg(2/(-1)) = 116,57° (с учётом квадранта). В Mathcad стоит использовать функцию arg(s), чтобы избежать ошибок при учёте знаков действительной и мнимой частей.
В обработке сигналов для определения сдвига фаз между гармоническими сигналами с комплексными амплитудами A = 5 — 5i вычисляют аргумент через arctg(-5/5) = -45°. Mathcad автоматически определит угол в нужном квадранте, что облегчает точные расчёты фазового сдвига.
При расчёте передачи электроэнергии по линии с комплексным коэффициентом передачи T = 0,8 + 0,6i важно определить фазовый угол сигнала на выходе. В Mathcad arg(T) даст значение примерно 36,87°, что позволяет оценить фазовый сдвиг между входом и выходом линии.
Для решения задач в радиотехнике при анализе комплексных коэффициентов отражения Γ = -0,3 + 0,4i аргумент позволяет определить фазу отражённой волны. Расчёт в Mathcad с использованием arg(Γ) даст угол порядка 126,87°, что важно для оценки эффективности согласования цепей.
Вопрос-ответ:
Как в Mathcad вычислить аргумент комплексного числа?
В Mathcad для определения аргумента комплексного числа используется функция arg(z), где z — это заданное комплексное число. Она возвращает угол в радианах, который образует вектор комплексного числа с положительным направлением оси действительных чисел. Этот угол отражает фазу числа.
Можно ли получить аргумент комплексного числа в градусах вместо радианов в Mathcad?
По умолчанию функция arg(z) в Mathcad выдаёт значение угла в радианах. Чтобы получить аргумент в градусах, нужно результат функции arg(z) умножить на константу 180/π. Таким образом, формула будет выглядеть так: градусы = arg(z) * 180 / π.
Как Mathcad обрабатывает вычисление аргумента, если комплексное число лежит на отрицательной действительной оси?
Когда комплексное число находится на отрицательной части действительной оси, то есть его значение равно, например, -a + 0i (где a > 0), функция arg(z) возвращает значение ±π (180 градусов), в зависимости от направления вектора. В Mathcad это обычно обозначается как π радиан. Это отражает факт, что вектор направлен в противоположную сторону от положительной оси.
Как использовать аргумент комплексного числа для решения инженерных задач в Mathcad?
Аргумент комплексного числа часто применяется для анализа фазовых сдвигов в электротехнике и системах управления. В Mathcad, вычисляя arg(z), можно определить фазу сигнала или отклика системы. Это позволяет, например, оценить задержку по фазе между входным и выходным сигналами или понять поведение колебательных процессов. Значение аргумента помогает строить диаграммы фаз и проводить точные расчёты в технических проектах.
Как проверить корректность вычисления аргумента комплексного числа в Mathcad?
Для проверки можно вручную вычислить угол с помощью функции atan2(im, re), где im — мнимая часть, а re — действительная часть числа. В Mathcad atan2 обычно встроена и позволяет получить фазу с правильным учётом знаков обеих частей. Сравнив значение arg(z) и atan2(im, re), можно убедиться в точности вычисления. Также полезно тестировать вычисления на простых числах, например, 1 + 0i, 0 + i, -1 + 0i, чтобы оценить корректность результата.
Как в Mathcad получить аргумент комплексного числа и какие функции для этого используются?
В Mathcad для определения аргумента комплексного числа применяется функция arg(z), где z — заданное комплексное число. Эта функция возвращает угол в радианах между положительным направлением оси действительных чисел и вектором, который представляет комплексное число в комплексной плоскости. Важно учитывать, что результат arg(z) обычно находится в диапазоне от -π до π, что соответствует стандартному определению аргумента. Кроме того, можно использовать функцию atan2(Im(z), Re(z)), которая более явно рассчитывает угол с учётом знаков действительной и мнимой частей, что позволяет избежать ошибок при вычислении аргумента в разных квадрантах.
Почему при вычислении аргумента комплексного числа в Mathcad иногда получаются неожиданные значения и как этого избежать?
Некорректные значения аргумента могут появиться, если использовать функции, не учитывающие квадрант комплексного числа, например, если рассчитывать аргумент как arctg(Im/Re), то результат будет в пределах от -π/2 до π/2, что не всегда соответствует реальному положению точки на комплексной плоскости. В Mathcad лучше применять функцию arg(z) или atan2, которые учитывают знаки обеих частей. Также важно проверять, что входное число действительно комплексное и корректно задано в Mathcad. При работе с комплексными выражениями иногда бывает полезно явно выделять действительную и мнимую части, чтобы избежать ошибок в вычислениях, особенно если они получены в результате сложных операций.