В Mathcad создание дискретных переменных с нестандартным шагом осуществляется с помощью векторных операций и встроенных функций. Вместо стандартного равномерного шага 1 или фиксированного значения, можно задать шаг как отдельный вектор или вычисляемое выражение, что расширяет возможности моделирования.
Для построения такой переменной используют оператор диапазона с добавлением математических операций, например, start + step * индекс. Важным моментом является корректный выбор длины вектора индексов, чтобы итоговый массив не выходил за нужные границы.
Рекомендуется проверять тип и размерность результата после вычисления, так как Mathcad чувствителен к несовпадению размерностей. Применение функции length() и конструкций if позволяет автоматизировать контроль границ и избежать ошибок при работе с динамическими шагами.
Создание массива значений с заданным нестандартным шагом
В Mathcad для формирования массива с произвольным шагом применяют функцию создания векторов с оператором двоеточия и дополнительными вычислениями. Если шаг отличается от стандартного равномерного увеличения на 1, используют выражение с формулой, задающей необходимый шаг.
Например, для массива с элементами от a до b с шагом h используется запись: Array := a + h * (0..n), где n – количество элементов минус один. Значение n определяется по формуле n := floor((b - a)/h), что гарантирует попадание последнего элемента в заданный диапазон без превышения.
Для создания массива, где шаг изменяется по заданной закономерности (например, арифметическая прогрессия с переменным шагом), в Mathcad применяют оператор суммирования или пользовательские функции, возвращающие массив значений.
Для сложных нестандартных шагов стоит использовать пользовательскую функцию с параметром индекса i, вычисляющую значение каждого элемента. Затем массив строится через вектор индексов: Array := func(0..n).
Важно контролировать длину массива, чтобы не выходить за границы заданного диапазона. Использование функции floor для вычисления количества элементов помогает избежать включения значений за пределами b.
Таким образом, Mathcad позволяет гибко создавать дискретные переменные с любым шагом, используя арифметические операции и встроенные функции для работы с индексами и массивами.
Использование встроенных функций для генерации дискретных последовательностей

Оператор диапазона задаётся в формате начало, шаг, конец. Например, выражение 0, 0.5 .. 5 создаст вектор значений от 0 до 5 с шагом 0.5. Важно, что шаг задаётся явно, и Mathcad автоматически остановится при достижении или превышении значения конца. При этом точность вычислений сохраняется, если шаг дробный.
Функция seq позволяет более гибко формировать последовательности. Синтаксис: seq(функция, переменная, начало, конец, шаг). Здесь можно задавать сложные зависимости элементов, например, seq(i^2, i, 1, 10, 2) сгенерирует квадраты чисел с шагом 2: 1, 9, 25, …, 81.
Функция linspace создаёт линейно равномерно распределённые точки между двумя границами. В отличие от оператора диапазона, здесь шаг не задаётся напрямую, а определяется количеством точек. Например, linspace(0, 10, 21) создаст 21 точку от 0 до 10 с шагом 0.5. Это удобно, когда важен именно фиксированный размер массива.
Для дискретных последовательностей с неравномерным шагом можно комбинировать эти функции, используя, например, seq для задания формулы шага, или создавать массивы вручную через конкатенацию.
Важно учитывать, что при использовании оператора диапазона и функции seq шаг должен быть отличен от нуля и не должен приводить к бесконечным циклам. Рекомендуется проверять границы и шаги перед генерацией, чтобы избежать ошибок.
Для анализа и дальнейших вычислений с последовательностями Mathcad позволяет использовать встроенные функции фильтрации, суммирования и индексации элементов, что расширяет возможности работы с дискретными данными.
Обход ограничений стандартного оператора диапазона в Mathcad
Стандартный оператор диапазона в Mathcad (start..end) поддерживает только шаг равный 1. Для создания дискретных переменных с произвольным шагом требуется альтернативный подход.
Используйте функцию ВЕКТОР с параметрами начало, шаг и количество элементов. Формула выглядит так:
x := ВЕКТОР(начало, шаг, n), где n = FLOOR((конец — начало)/шаг) + 1. Это позволяет задать шаг любой величины и избежать округлений.
Другой способ – определить переменную как элемент-wise операцию с использованием индекса:
x[i := начало + (i-1)*шаг, где i изменяется по стандартному диапазону с шагом 1. Здесь шаг задаётся явно, а количество точек контролируется диапазоном индекса.
При работе с большим объёмом данных рекомендуют использовать второй метод – он эффективнее с точки зрения вычислений и уменьшает вероятность ошибок округления.
В случаях, когда шаг не является постоянным, можно применять рекурсивные или пользовательские функции, вычисляющие каждый следующий элемент по заданому правилу.
Таким образом, обход ограничений оператора диапазона сводится к использованию индексов и явного задания формулы для каждого элемента массива.
Построение графиков дискретных переменных с произвольным шагом
В Mathcad для построения графиков дискретных переменных с произвольным шагом используется вектор, задающий набор точек по оси X, и соответствующий вектор значений по оси Y. Шаг между элементами вектора X задаётся явно, например, с помощью оператора присваивания и функции генерации последовательности.
Чтобы определить дискретную переменную с шагом, отличным от единицы, применяют синтаксис:
X := начальное_значение, начальное_значение + шаг .. конечное_значение
Например, для шага 0.3 от 0 до 3 запись будет выглядеть так:
X := 0, 0.3 .. 3
После создания вектора X вычисляют значения функции Y, например:
Y := sin(X)
Построение графика выполняется через команду графика, где в качестве оси X передают сформированный вектор X, а в качестве оси Y – соответствующие значения Y. Mathcad корректно отображает точки с произвольным шагом, сохраняя дискретность.
Для улучшения восприятия при визуализации стоит использовать маркеры точек, отключив линию соединения, если важна именно дискретность. Это делается в настройках графика, где тип линии устанавливают как «нет».
В случае нескольких дискретных наборов с разными шагами рекомендуется задавать векторы X отдельно и синхронизировать оси по диапазону, чтобы сравнение было корректным.
Если шаг переменной меняется динамически, в Mathcad можно использовать объединение нескольких последовательностей через конкатенацию, создавая комбинированный вектор точек.
Использование произвольного шага даёт гибкость в построении точных дискретных моделей и позволяет наглядно отображать данные с разным разрешением на одном графике.
Автоматическое вычисление шага при заданных граничных условиях
Для определения дискретной переменной с произвольным шагом в Mathcad при известных границах диапазона необходимо задать стартовое значение, конечное и количество точек или желаемый шаг. При этом шаг может рассчитываться автоматически по формуле:
h = (xкон — xнач) / (N — 1),
где xнач – начальное значение, xкон – конечное, N – количество дискретных точек. Такой подход гарантирует равномерное распределение значений от начала до конца, включая обе границы.
Если количество точек N неизвестно, а шаг h задан, вычисление N следует выполнять как целую часть выражения:
N = floor((xкон — xнач) / h) + 1.
В Mathcad удобно использовать встроенные функции для округления и генерации векторов. Например, создавая вектор x с помощью диапазона от xнач до xкон с шагом h, Mathcad автоматически подберёт количество элементов.
Важно учитывать, что при вычислении шага по количеству точек следует избегать деления на ноль – проверять, что N ≥ 2. При необходимости точное попадание в конечную точку обеспечивается использованием интерполяции или корректировкой шага.
В случаях с неравномерным или адаптивным шагом можно использовать условия для изменения шага внутри цикла генерации значений, однако при строго заданных границах и равномерном шаге описанный способ является наиболее точным и простым в реализации.
Работа с векторами и матрицами для хранения дискретных данных
В Mathcad для представления дискретных данных оптимально использовать векторы и матрицы. Они позволяют компактно хранить наборы значений, легко выполнять операции с элементами и применять функции к массивам данных.
Особенности работы с векторами и матрицами при дискретных переменных с произвольным шагом:
- Определение вектора с произвольным шагом осуществляется через оператор диапазона с указанием начального значения, шага и конечного значения. Например,
x := 0,1..10создаст вектор с шагом 0.1 от 0 до 10. - Матрицы формируются из нескольких векторов или через явное перечисление элементов с помощью скобок и точек с запятой для строк, например,
A := [1, 2, 3; 4, 5, 6]. - Векторы можно использовать для хранения значений функции, вычисленной на дискретных точках:
y := f(x), где f – выражение, поддерживающее векторные операции. - Изменение шага требует пересоздания вектора, что влияет на размерность хранящихся данных. Для адаптивного шага рекомендуется создавать новые векторы при смене параметров.
Рекомендации по работе:
- Используйте векторы для одномерных наборов данных и матрицы для многомерных или табличных представлений.
- Обращайтесь к элементам по индексу:
x[3]– третий элемент вектора,A[2,1]– элемент во второй строке первого столбца. - Для вычислений с матрицами применяйте встроенные функции Mathcad: сумма по строкам и столбцам, транспонирование, умножение и т.д.
- При необходимости динамического изменения дискретизации используйте операторы создания новых векторов, а не попытки изменить шаг в уже созданном массиве.
- Для больших объемов данных оптимизируйте память, избегая избыточных копий векторов и матриц.
Применение циклов и пользовательских функций для создания дискретных наборов
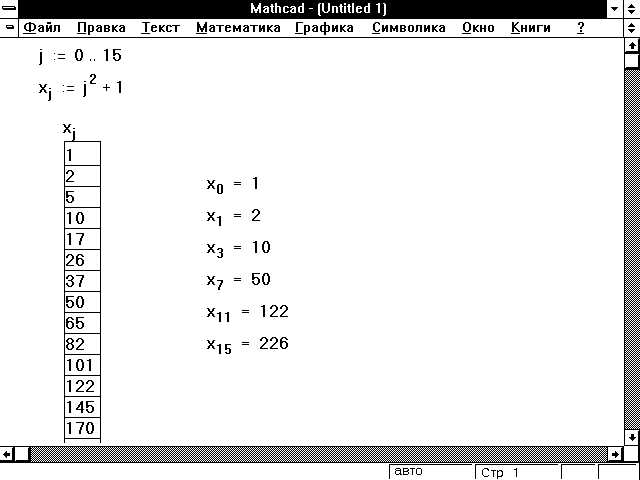
Для задания дискретных переменных с произвольным шагом в Mathcad можно использовать циклы и собственные функции, что расширяет возможности по формированию нестандартных последовательностей. Такой подход позволяет создавать наборы значений, которые невозможно получить стандартным определением с фиксированным шагом.
- Определение пользовательской функции:
- Функция принимает параметры: начальное значение, количество элементов и шаг.
- В теле функции применяется цикл
for, формирующий массив значений. - Возвращается готовый вектор, который можно использовать далее в вычислениях.
- Пример функции на Mathcad:
Seq(x0, n, h) :=local arr := vector(n)for i from 0 to n-1 doarr[i+1 := x0 + i * hend forreturn arr - Использование функции:
- Для создания набора с неравномерным шагом можно модифицировать шаг внутри цикла, задавая его формулой или массивом.
- Результирующий вектор легко интегрируется в графики, таблицы и дальнейшие вычисления.
- Рекомендации:
- Для оптимизации скорости вычислений используйте встроенные функции Mathcad, избегая избыточных операций внутри цикла.
- Если шаг меняется в зависимости от индекса, создавайте отдельный массив шагов и суммируйте их к начальному значению.
- Проверяйте корректность работы функции на небольших наборах перед применением к большим данным.
Вопрос-ответ:
Как в Mathcad задать дискретную переменную с произвольным шагом?
Для задания дискретной переменной с произвольным шагом в Mathcad обычно используют оператор диапазона с указанием начального значения, шага и конечного значения. Формат записи выглядит так: x := start, step .. end. Здесь start — начальное число, step — величина шага, а end — конечное значение переменной. Таким образом переменная x принимает значения, начиная с start, увеличиваясь на шаг step, пока не достигнет или не превысит end.
Можно ли задать отрицательный шаг для дискретной переменной в Mathcad? Как это сделать?
Да, Mathcad позволяет использовать отрицательный шаг при создании дискретной переменной. Для этого в определении переменной достаточно указать отрицательное значение шага. Например, если нужно создать последовательность от 10 до 0 с шагом -2, запись будет выглядеть так: x := 10, -2 .. 0. Переменная x в этом случае будет принимать значения 10, 8, 6, 4, 2, 0.
Что произойдет, если заданный шаг не равномерно делит интервал между начальным и конечным значением?
Если шаг не является точным делителем интервала между начальным и конечным значением, Mathcad сформирует последовательность с шагом, указанным в определении, пока следующий шаг не превысит конечное значение. То есть последний элемент последовательности может быть меньше конечного значения или совпадать с ним, но не выходить за пределы указанного интервала. Важно учитывать это при анализе результатов, чтобы избежать неожиданных значений на конце диапазона.
Как проверить и изменить шаг дискретной переменной после её создания в Mathcad?
Чтобы проверить шаг дискретной переменной, можно вывести на экран несколько первых значений этой переменной и вычислить разницу между соседними элементами. Если необходимо изменить шаг, достаточно изменить параметр шага в записи определения переменной. Например, если изначально было x := 0, 0.5 .. 5, и нужно поменять шаг на 0.2, то достаточно заменить 0.5 на 0.2: x := 0, 0.2 .. 5. После этого Mathcad пересчитает последовательность автоматически.
Можно ли использовать дискретные переменные с произвольным шагом в формулах и графиках Mathcad?
Да, дискретные переменные с произвольным шагом легко применимы в вычислениях и построении графиков. Их значения можно подставлять в формулы, вычислять функции от этих переменных, а затем отображать результаты на графиках. В Mathcad достаточно определить переменную с нужным шагом, затем использовать её в выражениях. Это позволяет строить графики с нужной дискретностью, что полезно при анализе и визуализации данных.
Как в Mathcad задать дискретную переменную с произвольным шагом, если шаг не равен единице?
В Mathcad для определения дискретной переменной с произвольным шагом можно использовать оператор присваивания с формулой, задающей последовательность значений. Например, если нужно создать переменную x, принимающую значения от a до b с шагом h, то можно написать выражение вида: x := a, a + h, a + 2*h, ..., b. При этом обычно применяют встроенную функцию или формируют вектор с помощью индексации и арифметической прогрессии, например: x := a + i*h, где i = 0..N, где N — количество шагов, рассчитанное исходя из диапазона и величины шага. Такой способ позволяет гибко задавать дискретные переменные без ограничения на шаг.
Можно ли в Mathcad автоматически изменить шаг дискретной переменной в зависимости от условий внутри вычислений?
Да, в Mathcad можно менять шаг дискретной переменной, задавая его через выражение, зависящее от условий или других параметров. Для этого обычно создают функцию, которая вычисляет шаг в зависимости от входных данных, а затем формируют последовательность с этим динамическим шагом. Например, если шаг зависит от значения другой переменной или индекса, можно определить вектор с помощью цикла или встроенных функций, где каждый элемент вычисляется с учётом нужного шага. Такой подход полезен, когда требуется неравномерное распределение точек, например, при моделировании процессов с разной точностью в разных областях. Однако стоит учитывать, что последовательность должна быть корректно построена, чтобы избежать ошибок в вычислениях.