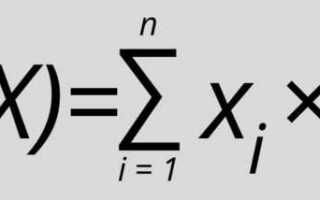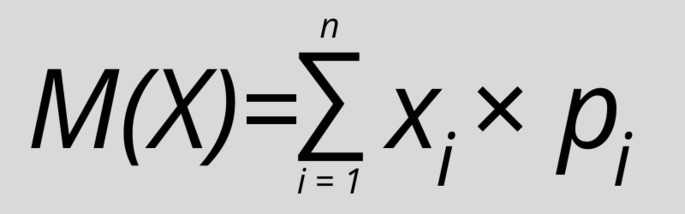
Математическое ожидание – ключевая характеристика случайной величины, отражающая среднее значение при большом числе повторений эксперимента. В Mathcad этот показатель вычисляется с помощью встроенных функций, позволяющих быстро и точно обрабатывать дискретные и непрерывные распределения.
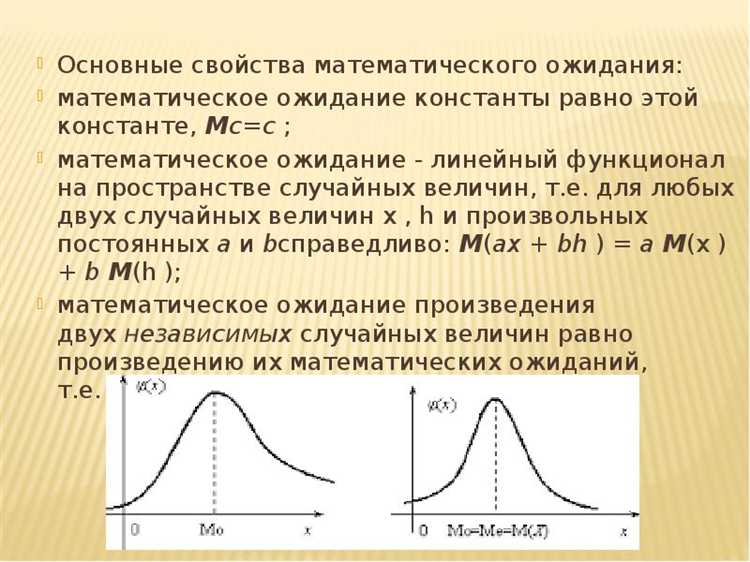
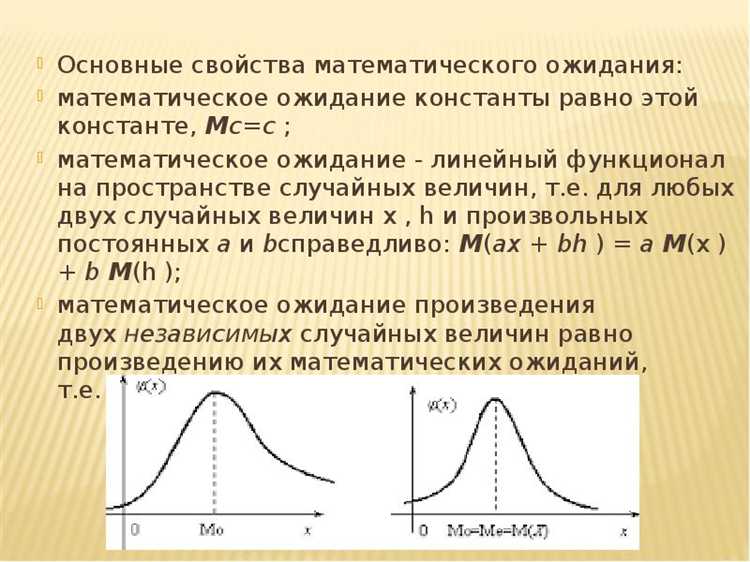
Для дискретных случайных величин в Mathcad применяют суммирование произведений значений переменной на соответствующие вероятности. Формулы реализуются через массивы данных и функции суммирования, что обеспечивает прозрачность вычислений и упрощает дальнейший анализ.
При работе с непрерывными распределениями Mathcad использует численное интегрирование по плотности вероятности. Важно правильно задать функцию плотности и границы интегрирования, чтобы получить корректный результат. Рекомендуется использовать стандартные библиотеки Mathcad для построения плотностей и проверять корректность заданных параметров перед расчетом.
Подготовка данных для расчёта математического ожидания в Mathcad
Для корректного вычисления математического ожидания в Mathcad требуется строго структурировать исходные данные и обеспечить их правильный формат. Основные шаги подготовки включают:
- Форматирование выборки значений случайной величины:
- Создайте в Mathcad вектор или матрицу, содержащую все наблюдения или значения случайной величины.
- Убедитесь, что тип данных числовой (вещественный или целочисленный) без пропусков и ошибок.
- Определение весовых коэффициентов (если используется взвешенное математическое ожидание):
- Создайте отдельный вектор вероятностей или весов, размер которого совпадает с размером выборки.
- Сумма всех весов должна равняться 1 для корректной интерпретации вероятностей.
- Проверка соответствия размеров:
- Размеры векторов значений и весов должны совпадать, иначе вычисления вызовут ошибку.
- Используйте функцию size() для проверки размерности.
- Очистка данных:
- Удалите аномальные или пропущенные значения из исходных данных перед вводом в Mathcad.
- Используйте фильтрацию по критериям или функции очистки в Mathcad.
- Оптимизация вычислений:
- Для больших наборов данных используйте упрощённые выражения и избегайте дублирования данных.
- Предварительно рассчитайте необходимые промежуточные показатели вне основного вычислительного блока.
Тщательная подготовка данных гарантирует точность и стабильность результата при расчёте математического ожидания в Mathcad.
Создание массива случайных величин в Mathcad
В Mathcad генерация массива случайных величин реализуется с помощью встроенной функции random. Для формирования массива необходимо задать размерность и диапазон значений.
- Определение размера массива: используйте вектор или матрицу, например, для одномерного массива n элементов создайте вектор переменной индексов i := 0..n-1.
- Генерация случайных чисел: функция random() возвращает случайное число из интервала [0; 1). Для получения чисел в другом диапазоне применяйте линейное преобразование:
random() * (b — a) + a, где a – нижняя граница, b – верхняя. - Формирование массива: используйте оператор поэлементного присваивания с индексом:
X[i := 0..n-1 := random() * (b — a) + a. - Многомерные массивы: создайте двумерный массив, задав диапазоны для каждого измерения, например:
X[i := 0..m-1, j := 0..n-1 := random() * (b — a) + a. - Фиксация семени генератора: для воспроизводимости результатов примените setseed(value), где value – целое число, задающее начальное значение генератора.
Таким образом, в Mathcad можно быстро создавать массивы случайных величин с нужным размером и диапазоном, что облегчает последующий расчет математического ожидания и других статистических параметров.
Использование встроенных функций Mathcad для вычисления среднего значения
В Mathcad вычисление математического ожидания выполняется с помощью встроенных функций, упрощающих работу с массивами данных. Для набора значений применяется функция mean(), которая автоматически рассчитывает среднее арифметическое элементов вектора или матрицы.
Для вычисления среднего значения по массиву данных достаточно задать переменную с набором чисел и вызвать mean(имя_массива). Если данные представлены в виде матрицы, функция возвращает среднее по всем элементам.
Для обработки выборок с весами используется функция sum() в комбинации с произведением значений и весов, что позволяет получить взвешенное среднее. В этом случае формула записывается как sum(значения * веса) / sum(веса).
Встроенные функции Mathcad работают с числовыми и символическими выражениями, что даёт возможность вычислять среднее значения как для конкретных данных, так и для параметрических выражений.
При работе с большими массивами рекомендуется предварительно проверить корректность ввода с помощью функции size() и визуально оценить данные, чтобы избежать ошибок при вычислении.
Использование mean() предпочтительно при стандартных задачах, а комбинирование sum() и арифметических операций – при более сложных вычислениях, требующих учёта дополнительных факторов.
Применение формулы математического ожидания к выборочным данным
Математическое ожидание выборки рассчитывается как средневзвешенное значение наблюдаемых величин. Для выборки из n элементов формула принимает вид: M = (1/n) ∑ xᵢ, где xᵢ – отдельные наблюдения.
В Mathcad вычисление математического ожидания основывается на встроенных функциях суммирования и деления. Следует строго использовать числовые векторы или массивы данных, чтобы избежать ошибок типов. Рекомендуется предварительно проверить полноту данных и исключить пропуски, так как они искажают среднее.
Для реализации формулы в Mathcad задайте вектор данных, затем используйте оператор суммирования sum(v) и делите на длину выборки length(v). При работе с большими наборами данных полезно применять функции обработки ошибок и фильтрации, чтобы исключить выбросы, влияющие на точность оценки.
Важно учитывать, что формула математического ожидания для выборочных данных предполагает равную вероятность каждого наблюдения. Если данные имеют разные веса, используйте взвешенное среднее, где каждый элемент умножается на соответствующий коэффициент вероятности.
Практическая рекомендация: проверяйте результаты расчёта через визуализацию распределения данных и сравнение с теоретическими значениями, если они известны. Это повысит надёжность интерпретации среднего и выявит аномалии в выборке.
Обработка дискретных и непрерывных распределений в Mathcad
Для дискретных распределений в Mathcad математическое ожидание вычисляется как взвешенная сумма значений случайной величины. Необходимо задать вектор значений X и соответствующий вектор вероятностей P, где сумма элементов P равна 1. Формула реализуется как МатематическоеОжидание := Σ (X[i] * P[i]). Важно проверить корректность нормировки вероятностей, используя функцию sum(P).
Для непрерывных распределений математическое ожидание определяется через интеграл по плотности вероятности. В Mathcad используется функция интегрирования int с заданной функцией плотности f(x) на заданном интервале. Пример: МатематическоеОжидание := int(x * f(x), x, a, b), где a и b – границы определения плотности. При численном интегрировании рекомендуется использовать достаточно мелкую дискретизацию или встроенные численные методы Mathcad для точности.
Для проверки корректности работы с непрерывными распределениями следует контролировать нормировку плотности: интеграл int(f(x), x, a, b) должен равняться 1. При заданных параметрах распределения можно использовать встроенные функции Mathcad для стандартных распределений (например, нормального, экспоненциального), что позволяет получить математическое ожидание напрямую через встроенные выражения.
Рекомендуется для повышения точности численного вычисления математического ожидания применять функции интерполяции и сглаживания, если исходные данные дискретны, но моделируют непрерывное распределение. В Mathcad это реализуется через встроенные функции работы с массивами и числовыми методами.
Проверка корректности результата математического ожидания через графики в Mathcad
Для оценки точности вычисленного математического ожидания в Mathcad целесообразно использовать графическую проверку. Один из эффективных способов – построение функции плотности вероятности (или гистограммы, если речь идет о дискретных данных) совместно с отображением линии математического ожидания.
1. Введите функцию плотности вероятности f(x) или набор данных X, по которому рассчитывается ожидание.
2. Постройте график плотности:
X := -10, -9.9..10 f(x) := (1 / sqrt(2·π)) · exp(-x² / 2) plot(X, f(X))
3. Вычислите математическое ожидание:
μ := ∫(x·f(x), x, -∞, ∞)
4. Добавьте на график вертикальную линию в точке μ:
line(x) := if x = μ then max(f(X)) else NaN plot(X, f(X), X, line(X))
Для дискретных выборок (например, при моделировании методом Монте-Карло) необходимо использовать гистограмму:
X := random(1, 10000) meanX := avg(X) hist(X, 20)
На гистограмме отображается частотное распределение. Добавьте вертикальную линию в точке meanX, чтобы убедиться, что она совпадает с центром распределения. Существенные отклонения от визуального центра указывают на ошибки в модели или входных данных.
Дополнительно рекомендуется построить график кумулятивной функции распределения (CDF), чтобы убедиться в симметричности распределения относительно ожидаемого значения. Используйте встроенные функции cumsum и plot для наглядного анализа.
При наличии многократных экспериментов рекомендуется построить серию графиков с наложением, используя разные цветовые схемы для оценки стабильности результата.
Автоматизация вычислений математического ожидания с помощью скриптов Mathcad
Для автоматизации вычислений математического ожидания в Mathcad удобно использовать встроенные функции и программные блоки. Один из ключевых инструментов – программный блок if–else, позволяющий задавать условия выборки, что особенно полезно при работе с выборочными данными и условными распределениями.
При работе с массивами данных, например, измерениями физической величины, удобно использовать встроенную функцию mean(A), где A – вектор наблюдений. Для дискретных распределений, где заданы значения X и соответствующие вероятности P, математическое ожидание вычисляется выражением sum(X·P). В этом случае необходимо предварительно нормализовать P, чтобы сумма элементов была равна единице: P := P / sum(P).
Для автоматизации повторяющихся вычислений создаётся пользовательская функция. Например:
Expectation(X, P) :=
(
P := P / sum(P);
return sum(X·P);
)
Такой подход позволяет быстро получать результат при изменении входных данных. Функцию можно использовать внутри других скриптов или интерфейсных элементов рабочего листа. В случае работы с непрерывными распределениями Mathcad поддерживает численное интегрирование: mean := ∫ x·f(x) dx в заданных пределах. Для автоматизации интегрирования применяется блок с использованием функции given и оператора find или интегральной функции int() с подстановкой аналитического выражения плотности вероятности.
При необходимости анализа нескольких распределений в цикле используется оператор for. Например, для набора плотностей вероятности:
for i ∈ 0..n-1
M[i := int(x·f[i](x), x, a, b)
Для отладки и проверки корректности результата полезно включать графическое отображение функции плотности и рассчитанного значения ожидания на графике, что делается с помощью стандартного инструмента plot.