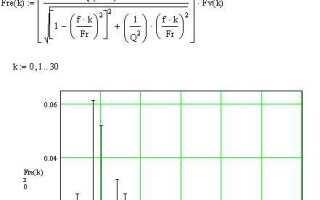Как построить амплитудный спектр сигнала в mathcad

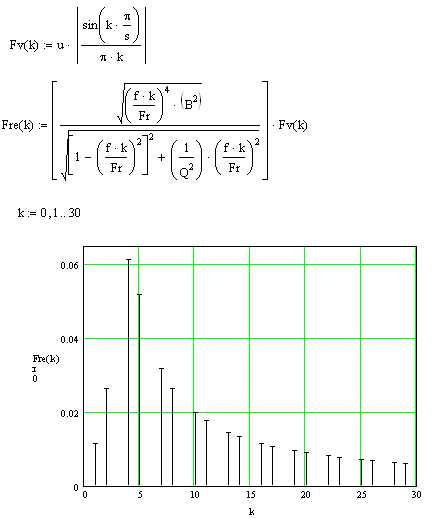
Для анализа частотного состава сигналов в Mathcad используется вычисление амплитудного спектра на основе преобразования Фурье. Практически любой дискретный сигнал можно представить в виде суммы синусоид с различными амплитудами и частотами, что позволяет выявить основные гармоники и спектральные компоненты.

В Mathcad ключевым элементом является применение встроенной функции FFT, обеспечивающей быстрое преобразование Фурье. Корректное использование этой функции требует соблюдения условий: равномерная дискретизация сигнала, длина массива – степень двойки, а также правильное масштабирование результата для получения физически значимых амплитуд.

Оптимальным подходом является предварительное выравнивание длины выборки с помощью дополнения нулями (zero padding), что повышает разрешающую способность спектра без искажения данных. Результат обработки отображается в виде графика амплитудного спектра, где по оси X откладывается частота, а по оси Y – амплитуда, выраженная в соответствующих единицах.

Реализация построения спектра в Mathcad включает создание векторов частот, нормализацию амплитуд и фильтрацию спектральных компонентов для выделения значимых гармоник. Это позволяет не только визуализировать, но и количественно оценить вклад каждой частоты в форму сигнала, что важно при анализе и обработке реальных данных.

Подготовка входных данных для анализа сигнала в Mathcad

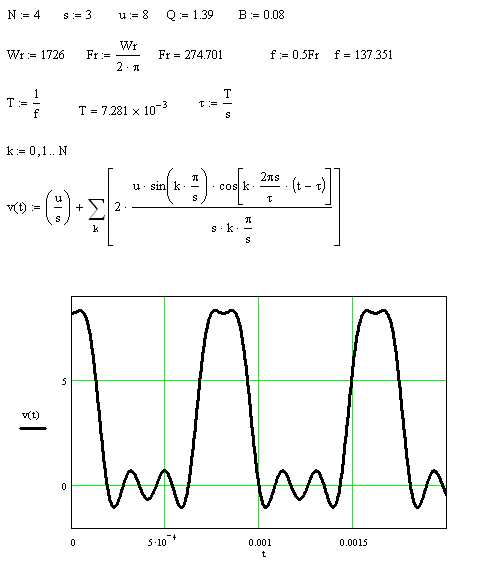
Для корректного построения амплитудного спектра важно обеспечить правильное форматирование и параметры входных данных в Mathcad.

Определите дискретизацию сигнала:
- Задайте частоту дискретизации Fs в герцах, соответствующую максимальной частоте сигнала (желательно в 2 раза выше по теореме Найквиста).
- Установите временную сетку t с равномерным шагом dt = 1/Fs.
Подготовьте вектор сигнала:
- Значения сигнала должны соответствовать временной сетке t и быть представлены в одномерном массиве.
- Длина массива должна быть степенью двойки для оптимизации алгоритма БПФ (Fast Fourier Transform).
Обеспечьте отсутствие тренда и постоянной составляющей:
- Перед анализом удалите среднее значение сигнала, вычтя его из всех точек.
- Если присутствуют низкочастотные тренды, примените фильтрацию или вычтите аппроксимирующую функцию.
Используйте оконные функции:
- Для снижения эффекта утечки спектра применяйте окна (например, Хэмминга, Ханна) к входным данным перед вычислением БПФ.
- Окно выбирается исходя из характеристик сигнала и требуемой точности спектра.
Проверьте корректность входных параметров:
- Убедитесь, что единицы измерения времени и частоты согласованы.
- Проверьте отсутствие пропусков и аномальных значений в сигнале.

Следование этим рекомендациям гарантирует получение точного и информативного амплитудного спектра при анализе сигнала в Mathcad.

Настройка параметров дискретизации и временной сетки

Для построения амплитудного спектра сигнала в Mathcad необходимо определить частоту дискретизации (Fs) и длительность временного интервала (T). Частота дискретизации должна быть минимум вдвое выше максимальной частоты сигнала (Fs ≥ 2·Fmax), чтобы избежать эффекта наложения спектров (aliasing). Для типичных аудиосигналов достаточно Fs = 44,1 кГц, для низкочастотных измерений – от 1 кГц.

Временной интервал выбирается с учетом желаемого разрешения по частоте: Δf = 1/T. Чем больше T, тем выше точность определения частотных компонентов. Рекомендуется устанавливать T так, чтобы длина выборки N = Fs·T была степенью двойки – это ускорит вычисление БПФ в Mathcad.

Временная сетка формируется равномерно: t = 0, 1/Fs, 2/Fs, …, (N-1)/Fs. Для создания массива точек используется встроенная функция Range с параметрами от 0 до (N-1)/Fs с шагом 1/Fs. Четкое соблюдение равномерности дискретизации обеспечивает корректность спектрального анализа.

При моделировании периодических сигналов важно выбирать временной интервал, кратный периоду сигнала, чтобы избежать спектральных утечек. Если период неизвестен, увеличение T позволяет улучшить спектральное разрешение и снизить влияние оконных эффектов.

Использование функции FFT для вычисления спектра сигнала

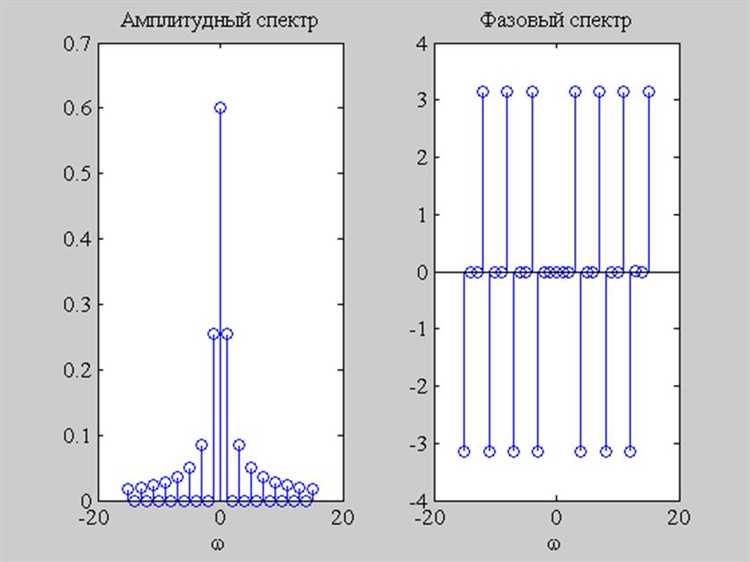
В Mathcad вычисление амплитудного спектра сигнала эффективно реализуется с помощью функции FFT (Fast Fourier Transform). Для корректного применения FFT необходимо учитывать следующие ключевые моменты:

Длина входного сигнала: Для оптимальной работы FFT длина массива данных должна быть степенью двойки (например, 256, 512, 1024). При необходимости сигнал дополняется нулями до ближайшей степени двойки (zero-padding).
Выбор временного интервала и частоты дискретизации: Задание правильного шага по времени (Δt) определяет максимальную частоту, которую можно адекватно проанализировать (частота Найквиста = 1/(2·Δt)).
Вызов функции FFT: В Mathcad FFT вызывается как fft(x), где x – массив отсчетов сигнала во временной области.
Преобразование результатов: Результат fft(x) – комплексный массив. Для амплитудного спектра требуется вычислить модуль каждого элемента: abs(fft(x)).
Нормировка амплитуд: Для получения правильных амплитуд спектра результат следует разделить на длину сигнала (N), то есть амплитуда = abs(fft(x))/N.
Половина спектра: Из-за симметрии преобразования Фурье по действительной оси обычно анализируется только первая половина спектра (от 0 до N/2).
Определение частотной оси: Частотные значения для спектра вычисляются по формуле f = (0..N/2) * Fs / N, где Fs – частота дискретизации.

Пример последовательности действий:

Задать массив сигналов с равномерным шагом по времени.
Вычислить FFT с помощью функции fft(x).
Взять модуль результата и нормировать на длину массива.
Выделить первую половину спектра.
Построить график амплитудного спектра по рассчитанной частотной оси.

Соблюдение этих рекомендаций обеспечивает точное и корректное построение амплитудного спектра сигнала в Mathcad без искажений и ошибок интерпретации.

Преобразование комплексного спектра в амплитудный

Комплексный спектр сигнала представлен набором комплексных чисел, каждое из которых соответствует определённой частоте и содержит информацию о амплитуде и фазе гармоники. Для построения амплитудного спектра необходимо вычислить модуль каждого комплексного значения спектра.

В Mathcad комплексные числа представлены в виде Re + j·Im. Амплитуда на частоте f_i определяется как A(f_i) = √(Re(f_i)² + Im(f_i)²). Для оптимизации вычислений можно использовать встроенную функцию abs(), возвращающую модуль комплексного числа.

После получения амплитудных значений формируется вектор амплитудного спектра, который отображается графически. Рекомендуется нормировать амплитуды относительно максимального значения спектра для удобства анализа и сравнения сигналов разной мощности.

Важно учитывать, что при вычислении амплитудного спектра спектр часто усредняют или фильтруют для снижения влияния шума. В Mathcad для этих целей применяются функции сглаживания или фильтры скользящего среднего, встроенные в стандартные библиотеки.

При обработке результатов Фурье-преобразования следует исключать из анализа зеркальные компоненты спектра, возникающие из-за симметрии ДПФ, если рассматривается реальный сигнал. В этом случае амплитудный спектр строится только по положительным частотам, что уменьшает вычислительную нагрузку и улучшает читаемость графика.

Настройка отображения амплитудного спектра на графике

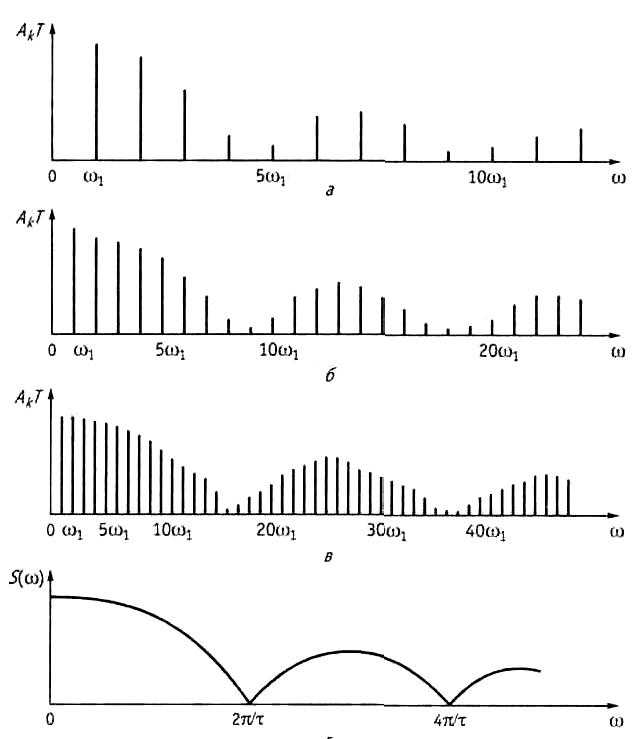
Для точного анализа амплитудного спектра в Mathcad необходимо грамотно настроить параметры графика. В первую очередь следует задать корректный диапазон оси частот. Рекомендуется использовать интервал от 0 до половины частоты дискретизации (Fs/2), так как спектр сигнала симметричен и выше этой границы данные избыточны.

Для улучшения читаемости спектра стоит увеличить масштаб по оси амплитуд. Оптимальным считается установка максимума амплитуды с запасом 10–20% выше максимального значения спектра. Это предотвращает обрезку пиков и обеспечивает видимость мелких деталей.

Настройка сетки на графике помогает быстро ориентироваться по значениям частот и амплитуд. В Mathcad рекомендуется включать вертикальные линии сетки с шагом, равным 10% от максимальной частоты, и горизонтальные – с шагом около 10% от максимальной амплитуды. Такая регулярность облегчает интерпретацию спектра.

Цвет и толщина линии графика влияют на восприятие данных. Для спектров с широким диапазоном амплитуд следует использовать линию толщиной не менее 2 пикселей и контрастный цвет, например, синий или черный. При отображении нескольких спектров задавайте разные цвета, чтобы избежать путаницы.

Подписи осей обязаны содержать единицы измерения: «Частота, Гц» для оси X и «Амплитуда» для оси Y. Добавление заголовка графика, отражающего источник сигнала или параметры преобразования Фурье, повышает информативность визуализации.

При необходимости построения спектра с логарифмической шкалой по амплитуде в Mathcad настройте ось Y на логарифмический масштаб, что позволит лучше видеть слабые компоненты сигнала, особенно при большом динамическом диапазоне.

Обработка и сглаживание амплитудного спектра

После вычисления амплитудного спектра с помощью БПФ в Mathcad, результат часто содержит шумовые выбросы и паразитные пики, затрудняющие анализ. Для устранения этих искажений рекомендуется применять методы сглаживания, основанные на свёртке спектра с ядром фильтра.

Наиболее эффективный подход – использование скользящего среднего. В Mathcad реализуется через функцию smooth(v, n), где v – вектор спектральных значений, n – длина окна. Оптимальное значение n подбирается экспериментально: при n = 5...15 достигается баланс между уменьшением шума и сохранением резких переходов.

Альтернативный способ – свёртка с гауссовым ядром. В Mathcad можно задать дискретное гауссово окно w := exp(-((i - N/2)^2)/(2σ^2)), нормировать его и выполнить операцию свёртки: v_smooth := conv(v, w). Значение σ определяет степень сглаживания, обычно выбирается в диапазоне 1–3 при длине окна 21–41 точек.

Удаление зеркальных и краевых эффектов выполняется отсечением соответствующих участков спектра после фильтрации. При работе с реальными сигналами желательно предварительно применять окно Хэннинга или Блэкмана к времному сигналу до выполнения БПФ для снижения спектральных артефактов.

Для оценки эффективности сглаживания рекомендуется построение логарифмического спектра: 20·log10(v_smooth). Это позволяет лучше выявить подавленные компоненты и сравнить форму спектра до и после фильтрации.

Экспорт и сохранение результатов анализа спектра

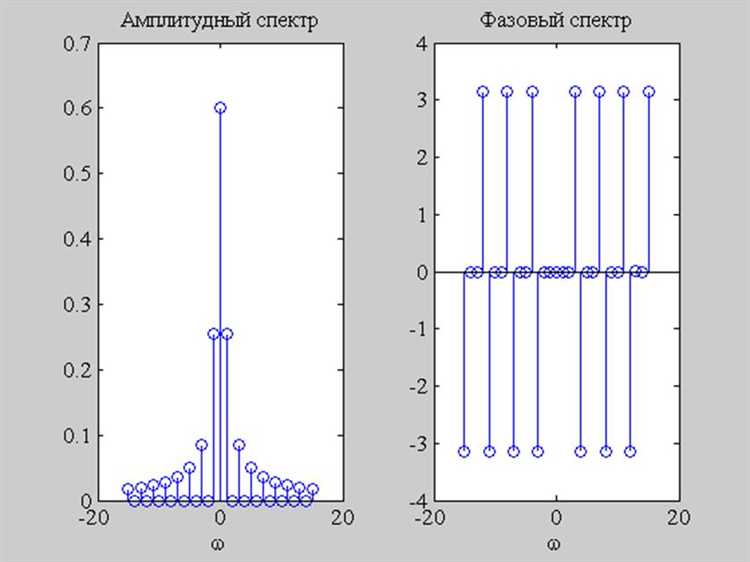
Для сохранения амплитудного спектра в Mathcad оптимально использовать функции WRITEPRN или EXPORT. Первая позволяет выгрузить массивы данных в текстовый файл с расширением .txt, вторая – в формат .csv, удобный для последующего анализа в Excel или MATLAB.

Результаты спектрального анализа формируются в виде вектора частот f и соответствующего амплитудного спектра A(f). Перед экспортом необходимо убедиться, что оба вектора имеют одинаковую длину и синхронизированы. Для записи используйте выражение:

WRITEPRN(«spectrum.txt», stack(f, A))

Для экспорта в .csv предпочтительнее:

EXPORT(«spectrum.csv», stack(f, A))

Графики можно сохранить через контекстное меню – Save As → Image, выбирая формат .png или .emf для векторной графики. Это важно при включении результатов в отчёты или научные публикации.

Автоматизация экспорта возможна через скрипты на VBScript или встроенные функции Mathcad API, позволяющие сохранить результаты анализа при каждом запуске рабочей области. Это удобно при работе с пакетной обработкой сигналов.

Для архивирования рекомендуется сохранять как данные, так и саму рабочую область Mathcad в формате .mcdx, особенно если использованы пользовательские функции или специфическая дискретизация спектра.