Для точного анализа динамических систем важно построить фазовый портрет, отображающий поведение решений в фазовом пространстве. Maple предоставляет инструменты для визуализации траекторий, однако правильная последовательность действий существенно облегчает работу и повышает качество результатов.
Первым шагом необходимо задать систему дифференциальных уравнений в формате, совместимом с командой dsolve. Важно использовать векторный вид системы, чтобы избежать ошибок при вычислениях и отображении. Затем следует определить параметры и диапазон переменных, учитывая характер системы – устойчивость, наличие точек равновесия и тип критических точек.
Основная команда для построения фазового портрета – DEplot из пакета DEtools. Рекомендуется заранее настроить плотность сетки и длину траекторий, чтобы получить информативный график без излишней нагрузки на систему. При необходимости задайте начальные условия для ключевых точек, чтобы выделить особенности динамики.
Подготовка системы дифференциальных уравнений для анализа
Перед построением фазового портрета в Maple необходимо привести систему к удобному для анализа виду. Начинайте с явного задания уравнений в форме производных: diff(x(t), t) = f(x, y), diff(y(t), t) = g(x, y). Убедитесь, что функции f и g выражены через переменные, а не через производные или параметры, которые не определены.
Если система содержит параметры, рекомендуется присвоить им численные значения для упрощения визуализации и исключения неопределённостей. Для аналитических исследований можно оставить параметры символическими, но тогда при построении фазового портрета следует использовать конкретные числовые значения.
Проверьте систему на наличие сингулярных точек, решая уравнения f(x, y) = 0 и g(x, y) = 0. В Maple используйте команды solve или fsolve для поиска критических точек. Это важно для правильного определения устойчивости и направления векторного поля.
Для удобства работы с системой задайте переменные как функции времени: x := x(t), y := y(t). Это позволит использовать встроенные функции Maple для дифференцирования и интегрирования без ошибок.
При необходимости упростите уравнения с помощью Maple-команды simplify или expand, чтобы устранить избыточные выражения и повысить скорость вычислений.
Наконец, подготовьте систему в виде векторного поля, создав список или массив функций правых частей, например, V := [f(x, y), g(x, y)]. Это позволит использовать стандартные процедуры Maple для построения направлений потоков и фазовых траекторий.
Ввод уравнений в среду Maple и проверка синтаксиса
Для построения фазового портрета необходимо корректно задать систему дифференциальных уравнений. В Maple уравнения вводятся с использованием оператора :=, при этом каждая переменная и производная должны быть явно обозначены. Например, для системы dx/dt = f(x, y) и dy/dt = g(x, y) задайте:
eq1 := diff(x(t), t) = f(x(t), y(t));
eq2 := diff(y(t), t) = g(x(t), y(t));
Для проверки синтаксиса воспользуйтесь командой is() или просто выполните ввод уравнения в отдельной строке. Ошибки синтаксиса Maple сразу укажет при выполнении. Важно не пропускать круглые скобки у функций и оператор diff, так как их отсутствие приводит к ошибкам.
При использовании параметров или сложных выражений рекомендуется разбивать уравнения на части с помощью вспомогательных переменных, чтобы облегчить отладку. Например:
F := x(t)^2 — y(t);
G := x(t) + y(t)^2;
eq1 := diff(x(t), t) = F;
eq2 := diff(y(t), t) = G;
Обязательно проверяйте, что все переменные и функции согласованы по времени: x(t) и y(t), а не просто x или y. Отсутствие аргументов у функций часто становится источником ошибок.
Для быстрого выявления синтаксических проблем используйте команды restart; для сброса сессии и ввод уравнений заново. В случае ошибок Maple выделит проблемное место и предоставит пояснения.
Использование пакета DEtools для анализа динамики системы
Пакет DEtools в Maple предоставляет набор специализированных команд для детального анализа систем дифференциальных уравнений, что облегчает построение фазового портрета. Его применение позволяет выявить устойчивость критических точек, построить направления потоков и провести качественный разбор без необходимости решать систему аналитически.
- Импорт и подготовка системы:
Для начала нужно загрузить пакет командой
with(DEtools):. Затем определить систему в виде списка уравнений, например,sys := {x' = f(x,y), y' = g(x,y)};. - Нахождение критических точек:
Используется команда
CriticalPoints(sys, [x,y]), которая автоматически решит систему уравнений равновесияf(x,y)=0, g(x,y)=0. Это позволяет избежать ручного решения и сократить время анализа. - Локальный анализ устойчивости:
Для каждой критической точки удобно применять
Linearize(sys, [x,y], [x0,y0]), где[x0,y0]– координаты точки. Команда вычисляет якобиан и линейную систему, что дает матрицу для дальнейшего изучения собственных значений. - Собственные значения и типы точек:
С помощью
Eigenvalues()от якобиана можно определить тип равновесной точки (узел, седло, фокус). Это позволяет классифицировать поведение траекторий в окрестности точки. - Построение направлений векторного поля:
Команда
DEplot(sys, [x,y], t=a..b, arrows=medium)создаст фазовый портрет с векторными стрелками, отображая направление движения в фазовом пространстве. Параметрarrowsрегулирует плотность стрелок. - Автоматическое построение фазового портрета:
Использование
PhasePortrait(sys, [x,y], t=a..b)позволяет получить полный обзор динамики с учетом всех критических точек и направлений, включая траектории, устойчивость и граничные поведения.
Использование DEtools значительно упрощает построение качественного фазового портрета и позволяет сосредоточиться на интерпретации результатов, не отвлекаясь на вычислительные детали.
Определение и вычисление критических точек системы
f(x, y) = 0,
g(x, y) = 0.
В Maple для поиска критических точек используется команда solve. Например, solve({f(x,y)=0, g(x,y)=0}, {x,y}) возвращает список точек (x,y), где система стационарна.
Если уравнения нелинейные, предпочтительно использовать fsolve для численного решения, особенно при наличии сложных корней или нескольких решений. В этом случае задайте область поиска для повышения точности.
Рекомендуется проверить каждое найденное решение подставкой в исходные функции, чтобы исключить артефакты вычислений. После нахождения критических точек необходимо исследовать их устойчивость, что выполняется через якобиан системы, но это выходит за рамки данного раздела.
Построение направленного поля в Maple
Для построения направленного поля в Maple используется команда DEtools[fieldplot], которая визуализирует векторы скорости системы дифференциальных уравнений. Начните с определения системы в виде двух уравнений первого порядка, например:
sys := {diff(x(t), t) = f(x(t), y(t)), diff(y(t), t) = g(x(t), y(t))};
Далее вызовите направленное поле в заданной области:
DEtools[fieldplot](sys, [x(t), y(t)], x = a..b, y = c..d, arrows = medium, steps = 20);
Параметры arrows регулируют размер стрелок, а steps – плотность сетки. Для улучшения читаемости можно изменить цвет и толщину стрелок через дополнительные опции color и thickness. Если система задана в явном виде, можно определить функцию для правой части и передать её напрямую:
f := (x, y) -> ... ; g := (x, y) -> ... ;
DEtools[fieldplot]([f, g], x = a..b, y = c..d, steps = 25);
Перед построением рекомендуется проверить, что функции не имеют разрывов и особенностей в выбранной области, чтобы избежать искажений графика. Для более детального анализа комбинируйте направленное поле с фазовыми траекториями, используя функцию DEplot на тех же осях.
Настройка параметров графика фазового портрета

В Maple для построения фазового портрета используют функцию DEplot из пакета DEtools. Основные параметры, влияющие на визуализацию, задаются непосредственно при вызове этой функции.
Ключевые настройки:
Диапазон переменных: устанавливается через параметр [[x, xmin, xmax], [y, ymin, ymax]]. Для точного анализа рекомендуется выбирать диапазон, охватывающий интересующие области динамики. Например, [[x, -5, 5], [y, -5, 5]].
Начальные условия: задаются списком точек в параметре initialconditions. Для комплексного портрета лучше использовать несколько начальных точек, например, {[x=1, y=0], [x=-1, y=2]}.
Параметры интегрирования: параметр stepsize регулирует точность численного решения. Значение 0.01 обеспечивает плавность траекторий без чрезмерных затрат времени. Параметр maxsteps ограничивает число шагов, например, 5000.
Отрисовка направлений: для отображения векторного поля используется опция field=true. Толщину стрелок и цвет можно настраивать через arrowsize и color.
Визуальные параметры графика: для настройки осей применяются стандартные опции axes=boxed, labels=["x","y"], scaling=constrained. Цвета и стиль линий задаются через color и linestyle, что помогает выделить важные траектории.
Пример вызова:
DEplot({diff(x(t),t)=y(t), diff(y(t),t)=-x(t)}, {x,y}, t=0..10, initialconditions={[x=1,y=0]}, stepsize=0.01, maxsteps=5000, field=true, arrowsize=0.05, color=blue, axes=boxed, labels=["x","y"], scaling=constrained)
В итоговом графике важно обеспечить баланс между детализацией и читаемостью. Для сложных систем целесообразно строить несколько портретов с разными параметрами масштабирования и начальных условий, чтобы выявить ключевые особенности динамики.
Визуализация траекторий решений и их интерпретация
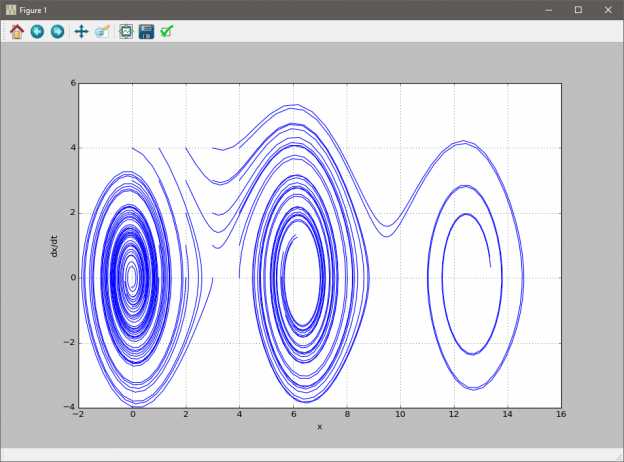
Параметры odeplot следует настраивать так, чтобы временной интервал был достаточен для раскрытия динамики: t – от 0 до значения, где траектории стабилизируются или проявляют устойчивое поведение. Для сложных систем полезно варьировать шаг интегрирования, чтобы избежать пропуска ключевых особенностей.
При интерпретации обращайте внимание на устойчивость точек равновесия, которая визуально проявляется через поведение близлежащих траекторий: сходятся к точке – устойчивый узел или фокус, расходятся – неустойчивый. Периодические орбиты обозначают циклы или устойчивые предельные циклы, их можно выявить, анализируя замкнутые траектории.
Для повышения информативности используйте различные цвета и толщину линий для разных типов решений и начальных условий. Подписи осей и легенды облегчают анализ и сравнение результатов. В Maple можно объединять несколько odeplot в одном графике с помощью display.
Автоматическая генерация сетки начальных условий с помощью цикла и сохранение результатов в массив упрощают экспериментирование с параметрами системы и изучение переходов между режимами динамики. Визуальный анализ фазового портрета дополняйте проверкой аналитических результатов, чтобы избежать неверных интерпретаций.
Сохранение и экспорт готового фазового портрета

Для сохранения фазового портрета в Maple рекомендуется использовать встроенные функции экспорта графиков. После построения портрета выполните следующие шаги:
- Выделите окно с графиком фазового портрета.
- В верхнем меню выберите
File→Export→Export Plot. - В открывшемся диалоговом окне укажите формат файла:
- PNG – оптимально для публикаций и презентаций, сохраняет высокое качество и поддерживает прозрачность.
- PDF – подходит для печати и векторной графики, сохраняет масштабируемость без потери качества.
- EPS – предпочтителен для профессиональной верстки и дальнейшей обработки в векторных редакторах.
- Установите разрешение (dpi) для растровых форматов. Для экранного использования достаточно 150-200 dpi, для печати – не менее 300 dpi.
- Укажите имя файла и путь сохранения, учитывая структуру проекта для удобства дальнейшей работы.
Кроме графического экспорта, для автоматизации сохранения используйте команды Maple:
plot()в сочетании сsaveпозволяет сохранить график напрямую в файл.
Для интеграции фазового портрета в отчёты или презентации используйте экспорт в PDF или PNG с прозрачным фоном. Если требуется дальнейшая редактируемость, экспортируйте в векторные форматы (PDF, EPS) и корректируйте в специализированных редакторах.
Вопрос-ответ:
Каким образом можно задать систему дифференциальных уравнений в Maple для построения фазового портрета?
Для задания системы в Maple необходимо использовать команду с указанием уравнений и переменных. Обычно систему вводят через оператор «:=» или «sys:=», перечисляя уравнения в фигурных скобках. Например, для системы двух уравнений по переменным x(t) и y(t) записывают {diff(x(t), t) = f(x, y), diff(y(t), t) = g(x, y)}. Такой способ позволяет Maple распознать уравнения как систему для последующего анализа и построения фазового портрета.
Какие шаги требуются для визуализации траекторий в фазовом пространстве с помощью Maple?
После задания системы уравнений нужно использовать функцию, предназначенную для численного решения и построения траекторий, например, «dfieldplot» или «phaseportrait». Важно выбрать диапазон значений для переменных, чтобы определить область построения, а также начальные условия для решения. Можно задавать множество начальных точек, чтобы наглядно увидеть разные поведения системы. Затем Maple сгенерирует график, отображающий траектории решений в фазовом пространстве, что позволит оценить устойчивость и характер движения системы.
Как интерпретировать устойчивость равновесных точек на фазовом портрете, построенном в Maple?
Устойчивость равновесных точек определяется видом траекторий, сходящихся к этим точкам или расходящихся от них. На фазовом портрете в Maple устойчивые точки часто отображаются как точки, к которым сходятся все близлежащие траектории — это может быть узел или фокус с затухающими колебаниями. Неустойчивые точки характеризуются расходящимися от них траекториями. Анализ можно дополнить вычислением собственных значений якобиана системы в точке равновесия, что даст математическую основу для оценки характера устойчивости.
Можно ли в Maple автоматически находить равновесные точки системы перед построением фазового портрета?
Да, Maple позволяет искать стационарные точки системы при помощи команды, решающей уравнения f(x, y) = 0 и g(x, y) = 0, где f и g — правые части дифференциальных уравнений. Используют функции «solve» или «fsolve» для аналитического или численного поиска решений. Это упрощает анализ системы, так как после нахождения точек равновесия их можно использовать для построения фазового портрета и анализа поведения системы вблизи этих точек.