Функция Дирака, или дельта-функция, представляет собой обобщённую функцию, активно применяемую в теории сигналов, квантовой механике и системах управления. В Maple её реализация требует понимания особенностей символических вычислений и обращения с обобщёнными функциями. Встроенная функция Dirac доступна в пакете Student[Calculus1], однако её поведение может отличаться от привычного математического представления.
Для корректного моделирования дельта-функции в Maple рекомендуется использовать не только вызов Dirac(x), но и изучить взаимодействие с такими операциями, как свёртка, интегрирование и преобразования Лапласа. Например, при выполнении интеграла int(Dirac(x-a)*f(x), x = -infinity..infinity) результатом будет f(a), если Maple корректно распознал дельта-функцию в составе выражения. Это поведение критично при работе с физическими моделями и задачами анализа сигналов.
Особое внимание следует уделить точному синтаксису и активации нужных пакетов: with(Student[Calculus1]) обеспечивает доступ к функциям Dirac и Heaviside. Без подключения пакета система не распознает обозначения. При необходимости символьной визуализации дельта-функции в графиках, можно использовать plot с параметром discont=true, но важно помнить, что дельта-функция не является функцией в обычном смысле и отображается схематически.
Применение Maple для работы с функцией Дирака требует чёткого понимания её математической природы и особенностей реализации в системе. Ошибки в интерпретации, попытки численного моделирования или некорректная свёртка могут привести к неверным результатам. Поэтому важно тестировать выражения на простых примерах и проверять поведение системы в каждом конкретном случае.
Создание пользовательской процедуры для моделирования δ(x)
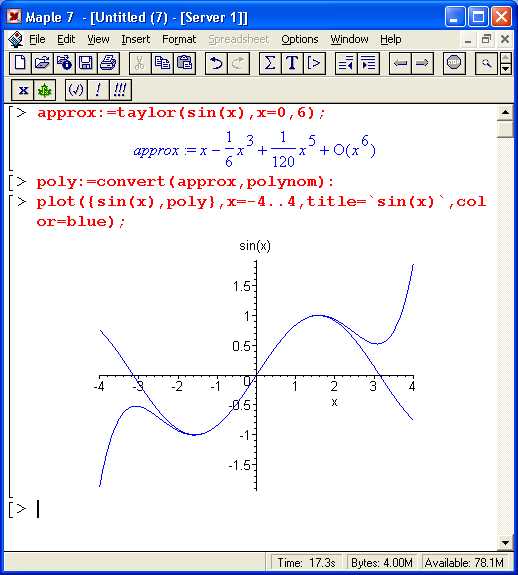
- Создайте модуль с параметром ε, контролирующим степень приближения к δ(x):
DiracApprox := proc(x, epsilon)
option inline;
piecewise(abs(x) < epsilon, 1/(2*epsilon), 0);
end proc;
- Для интегральных вычислений используйте команду `int` с явным указанием пределов:
int(DiracApprox(x, 0.01)*f(x), x = -1 .. 1);
- Аппроксимация корректно ведёт себя при ε → 0 и обеспечивает сходимость при численном интегрировании.
- Альтернатива – гауссовская аппроксимация, более гладкая, но требующая экспоненциальных вычислений:
DiracGaussian := proc(x, sigma)
option inline;
(1/(sqrt(Pi)*sigma)) * exp(-x^2 / sigma^2);
end proc;
- Проверка нормировки:
int(DiracGaussian(x, 0.01), x = -infinity .. infinity);
- Визуализация поведения δ(x):
plot(DiracGaussian(x, 0.05), x = -0.5 .. 0.5);
- Рекомендуется задавать ε или σ в пределах 10-2–10-4 для корректной имитации при численных операциях.
- Для устойчивости в численных задачах избегайте ε < 10-6, если не используется расширенная точность.
Процедуры позволяют использовать δ(x) в интегралах и визуализациях, сохраняя контроль над степенью аппроксимации.
Использование встроенных инструментов Maple для аппроксимации функции Дирака
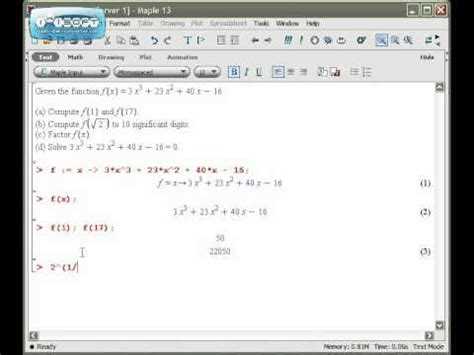
Для аппроксимации в Maple можно использовать следующий код:
with(plots):
sigma := 0.01:
f := x -> (1/(sqrt(2*Pi)*sigma))*exp(-x^2/(2*sigma^2)):
plot(f(x), x = -0.1 .. 0.1, discont = true);При необходимости варьировать степень приближения, параметр sigma можно уменьшать, но при этом возникает численная нестабильность. Maple поддерживает высокоточное вычисление при установке Digits на значения выше 20. Это особенно важно при анализе интегральных свойств аппроксимации.
Визуализация аппроксимированной дельта-функции удобна с помощью пакета plots, позволяющего задавать высокую точность отображения при помощи параметра numpoints. Например:
plot(f(x), x = -0.05 .. 0.05, numpoints = 1000);Для сравнения с дискретным представлением полезно использовать функцию `Heaviside` и производную от неё с помощью оператора `diff`, так как diff(Heaviside(x), x) в Maple возвращает Dirac(x). Однако для численного моделирования требуется замена на гладкие функции, например:
Heaviside_approx := x -> 1/(1 + exp(-x/sigma)):
diff(Heaviside_approx(x), x);Этот метод удобен для символьных и численных расчётов, когда необходимо встроить аппроксимацию дельта-функции в более сложные выражения или уравнения. Рекомендуется также использовать оператор `int` для проверки корректности нормировки аппроксимации на конечном интервале:
evalf(int(f(x), x = -infinity .. infinity));При правильно выбранном sigma интеграл стремится к 1, что подтверждает корректность аппроксимации.
Графическое представление приближений δ-функции
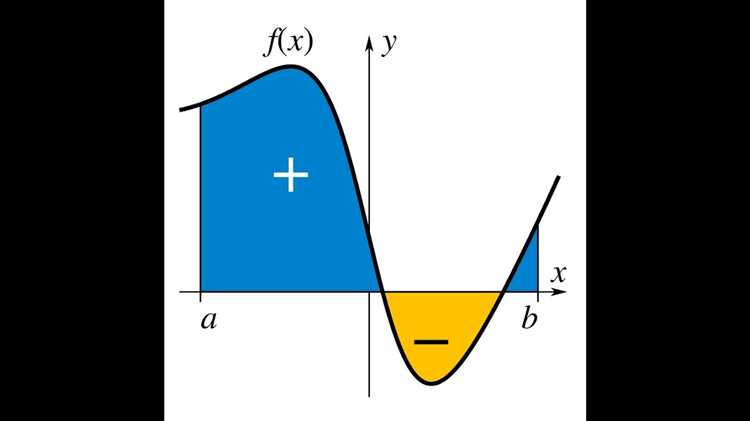
fn(x) = (n/π) / (1 + n²x²)
График данной функции в Maple строится командой:
plot((n/Pi)/(1 + n^2*x^2), x = -1 .. 1, n = 10..100, thickness = 2);
Для сравнения формы приближений рекомендуется варьировать параметр n в пределах от 10 до 1000. При увеличении n наблюдается сужение пика при сохранении площади под кривой, что соответствует свойству δ-функции.
Также полезно использовать нормированные гауссовы функции:
gσ(x) = (1 / (σ√(2π))) * exp(−x² / (2σ²))
В Maple визуализация выполняется через:
plot((1/(sigma*sqrt(2*Pi)))*exp(-x^2/(2*sigma^2)), x = -1 .. 1, sigma = 0.1..0.01);
Для анализа поведения при предельных значениях параметров эффективно использовать анимацию:
animate((n/Pi)/(1 + n^2*x^2), x = -1 .. 1, n = 1 .. 100);
Это позволяет отследить переход приближенной функции к δ-распределению. Рекомендуется использовать параметр grid = [200] для повышения точности отображения пиков.
Для всех графиков важно установить масштаб оси y вручную с помощью опции view = [xmin..xmax, ymin..ymax], чтобы избежать искажения формы при больших n.
Анализ интегралов с участием δ-функции в среде Maple
В Maple дельта-функция обозначается как Dirac(x). При интегрировании выражений, содержащих δ-функцию, следует учитывать её определяющее свойство: ∫ f(x)·δ(x−a) dx = f(a). Для корректного анализа необходимо использовать встроенные возможности Maple для обобщённых функций.
Рассмотрим пример:
int(f(x)*Dirac(x-a), x=-infinity..infinity);
Maple автоматически применит определение дельта-функции и вернёт результат f(a), при условии, что f(x) аналитически определена в точке x = a. Если функция f(x) содержит разрывы или неопределённости, необходимо использовать assuming или piecewise для уточнения условий интегрирования.
При работе с производными δ-функции, таких как diff(Dirac(x-a), x), Maple требует ручного управления правилами интегрирования по частям. Например, для вычисления:
int(f(x)*diff(Dirac(x-a), x), x=-infinity..infinity);
следует воспользоваться определением в распределительном смысле:
-int(diff(f(x), x) * Dirac(x-a), x=-infinity..infinity);
что возвращает -diff(f(x), x) | x=a. В таких случаях полезно явно указывать подстановку с использованием subs:
subs(x=a, -diff(f(x), x));
Для проверки корректности вычислений рекомендуется применять команду simplify совместно с assume:
assume(a, real); simplify(int(exp(x)*Dirac(x-a), x=-infinity..infinity));
Результатом будет exp(a). При работе с многомерными интегралами, например, int(Dirac(x)*Dirac(y), x=-1..1, y=-1..1), Maple возвращает 1, если область интегрирования включает точку (0,0), и 0 – в противном случае.
Использование пакета Physics повышает точность анализа, особенно при наличии производных дельта-функций. Перед началом расчётов следует активировать пакет:
with(Physics);
и установить режим использования обобщённых функций:
Setup(usedelta = true);
Это позволит Maple корректно обрабатывать правила интегрирования, включая интегралы с производными δ-функции и их свёртки.
Работа с производными и обобщёнными функциями в контексте δ(x)
В Maple производные δ-функции удобно выражаются через команду diff(Dirac(x), x). Например, чтобы вычислить δ′(x), используйте:
with(Physics):
diff(Dirac(x), x);
Для вычисления свёртки δ′(x) с функцией f(x), например, f(x) = exp(-x²), используйте:
f := x -> exp(-x^2):
int(diff(Dirac(x), x)*f(x), x = -infinity .. infinity);
Maple корректно применит правило интегрирования по частям и выдаст результат –f′(0). Для более высоких производных используйте diff(Dirac(x), x$n), где n – порядок производной. Следует учитывать, что прямое вычисление свёртки с такими производными требует ручного задания тестовой функции, поскольку Maple не проводит автоматическое упрощение обобщённых выражений без контекста.
Если необходимо использовать δ-функцию как производную ступенчатой функции, используйте связь δ(x) = D(Heaviside(x)). Пример для второй производной:
diff(Heaviside(x), x$2);
Результатом будет δ′(x), что подтверждает обобщённое определение. Это удобно при анализе распределений в задачах с разрывными правыми частями или импульсным воздействием.
Для визуализации приближений к δ(x) и её производным можно использовать сглаженные представления, например, гауссову аппроксимацию: δ_ε(x) = (1/(√π ε)) exp(–x²/ε²). В Maple это реализуется напрямую:
epsilon := 0.01:
delta_e := x -> (1/(sqrt(Pi)*epsilon))*exp(-x^2/epsilon^2):
plot([delta_e(x), diff(delta_e(x), x)], x = -0.1 .. 0.1);
Таким образом, Maple позволяет не только вычислять производные δ(x), но и проводить анализ с использованием обобщённых функций в прикладных и теоретических задачах. Корректная работа требует учёта функционального контекста, особенно при использовании интегралов и свёрток.
Решение дифференциальных уравнений с функцией Дирака в Maple
Для корректного моделирования дифференциальных уравнений с дельта-функцией Дирака в Maple необходимо задать эту функцию как обобщённую функцию. В системе используется пакет Student[Distribution], позволяющий работать с дельта-функцией через оператор Dirac().
При формулировке уравнения дельта-функция вводится явно, например:
diff(y(t), t) + y(t) = Dirac(t - t0), где t0 – момент воздействия импульса.
Решение получают с помощью команды dsolve, указывая начальные условия. Maple корректно интерпретирует дельта-функцию как распределение, обеспечивая разрывное поведение решения в точке t = t0.
Для контроля решения полезно проанализировать пределы функции в точке разрыва с помощью пределов слева и справа:
limit(y(t), t = t0, left) и limit(y(t), t = t0, right).
При численном решении (например, с dsolve/numeric) необходимо аккуратно задать сетку вычислений вокруг t0, чтобы избежать потери точности из-за импульсного воздействия.
Если уравнение содержит производные дельта-функции, Maple позволяет использовать Dirac(diff(t, n)) для обозначения производной порядка n. Это расширяет спектр решаемых задач, сохраняя точность и аналитическую корректность.
Вопрос-ответ:
Что такое функция Дирака и зачем её моделируют в Maple?
Функция Дирака — это обобщённая функция, которая часто используется в математике и физике для описания идеализированных точечных воздействий. В Maple её моделируют, чтобы выполнять вычисления с дельта-функцией и решать задачи, где важны точечные источники или мгновенные импульсы. Это позволяет работать с интегралами и дифференциальными уравнениями, где функция Дирака выступает как удобный инструмент.
Какие основные методы построения функции Дирака применяются в Maple?
В Maple функцию Дирака можно задавать с помощью различных подходов. Один из распространённых методов — использовать пределы последовательностей функций, которые сходятся к дельта-функции. Также часто применяют встроенные пакеты Maple, которые позволяют оперировать с обобщёнными функциями, включая Дирака, через обозначения и специальные операторы. Иногда используют приближения с помощью узких гауссовых пиков или прямоугольных функций для численных вычислений.
Как реализовать функцию Дирака для вычисления интегралов с её участием в Maple?
Для вычисления интегралов, включающих функцию Дирака, в Maple используют свойства дельта-функции, особенно её основное свойство — интеграл от произведения дельта-функции и произвольной функции равен значению этой функции в точке сосредоточения дельта-функции. В Maple это можно оформить через оператор `Dirac` из пакета `inttrans`. При подстановке в интеграл Maple автоматически применит это свойство и упростит выражение, что значительно облегчает вычисления.
Какие ограничения существуют при работе с функцией Дирака в Maple?
Несмотря на мощь Maple, функция Дирака остаётся обобщённой функцией, поэтому прямое численное её использование ограничено. В частности, нельзя просто подставить её значение в произвольную точку, как для обычной функции. Некоторые операции требуют аккуратного подхода и использования специальных команд или пределов. Кроме того, при численном моделировании функцию Дирака часто приближают с помощью функций с узкими пиками, что может влиять на точность результата.
Можно ли построить собственную аппроксимацию функции Дирака в Maple и как это сделать?
Да, можно. Один из способов — создать последовательность функций с узким и высоким пиком, которая при стремлении параметра к нулю будет приближать функцию Дирака. Например, можно использовать нормализованные гауссовы функции с уменьшающейся дисперсией. В Maple это реализуют, задавая параметр ширины и изучая поведение функции при его уменьшении. Такой подход полезен для численных вычислений и визуализации, позволяя понять, как дельта-функция проявляет себя в предельном случае.