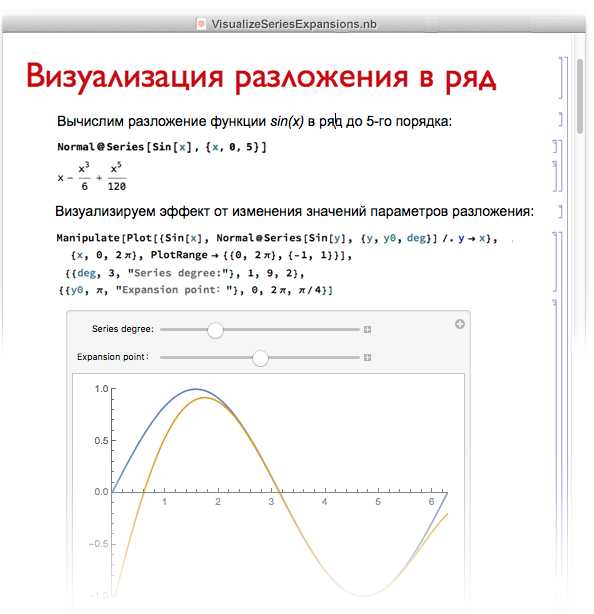
Wolfram Mathematica – это мощная система для математического моделирования, вычислений и визуализации данных, разработанная с акцентом на символьные и численные методы. Ее ядро построено на языке Wolfram Language, который сочетает выразительность и универсальность, позволяя решать задачи от простых уравнений до сложных алгоритмов машинного обучения.
Как установить и настроить Wolfram Mathematica на компьютере
Для установки Wolfram Mathematica зайдите на официальный сайт wolfram.com и создайте учетную запись Wolfram ID. После регистрации перейдите в раздел загрузок и выберите версию, соответствующую вашей операционной системе: Windows, macOS или Linux.
Скачайте установочный файл (обычно размер около 1.5–2 ГБ). Для Windows и macOS доступны стандартные инсталляторы, для Linux – архив с установочными скриптами. Перед запуском убедитесь, что в системе достаточно свободного места (минимум 4 ГБ) и обновлены драйверы графики, что улучшит производительность интерфейса.
Запустите установщик и следуйте подсказкам. Рекомендуется сохранить путь установки по умолчанию, чтобы избежать проблем с лицензированием. В процессе установки выберите опцию «Установить Wolfram Engine» и «Настроить Wolfram Kernel», если планируете работать с командной строкой.
После завершения установки откройте программу и войдите с помощью Wolfram ID для активации лицензии. При первом запуске автоматически загружаются необходимые библиотеки и обновления – дождитесь окончания процесса.
Для оптимальной работы настройте автосохранение в меню Preferences > Evaluation, установив интервал в 5 минут. Также в Preferences > Interface рекомендуется активировать опцию отображения синтаксиса и автодополнения, что ускорит набор кода.
Для расширения возможностей загрузите пакет Wolfram Cloud, если планируете работать с проектами онлайн, и активируйте интеграцию с другими Wolfram-продуктами через меню Add-ons. При использовании Mathematica в корпоративной среде настройте прокси-сервер через Preferences > Internet, чтобы избежать проблем с обновлениями и лицензированием.
Создание и сохранение первого документа в Wolfram Mathematica
Запустите Wolfram Mathematica и выберите File → New Notebook для создания нового документа. Рабочее пространство разделено на ячейки – в них вводится и выполняется код, а также добавляются текстовые комментарии.
Для начала введите простое выражение, например, 2+2, и нажмите Shift + Enter для выполнения. Результат отобразится сразу под ячейкой ввода.
Чтобы сохранить документ, перейдите в меню File → Save As…. Рекомендуется использовать формат .nb, который сохраняет структуру и позволяет в дальнейшем редактировать ячейки. Укажите понятное имя файла и выберите удобное расположение на диске.
Для регулярного сохранения используйте сочетание клавиш Ctrl + S (Windows) или Cmd + S (Mac). Это предотвращает потерю данных при сбоях.
При необходимости экспортируйте документ в формат .pdf через File → Save As Special → PDF. Это позволяет делиться результатами без необходимости открывать Mathematica.
Ввод и редактирование математических выражений
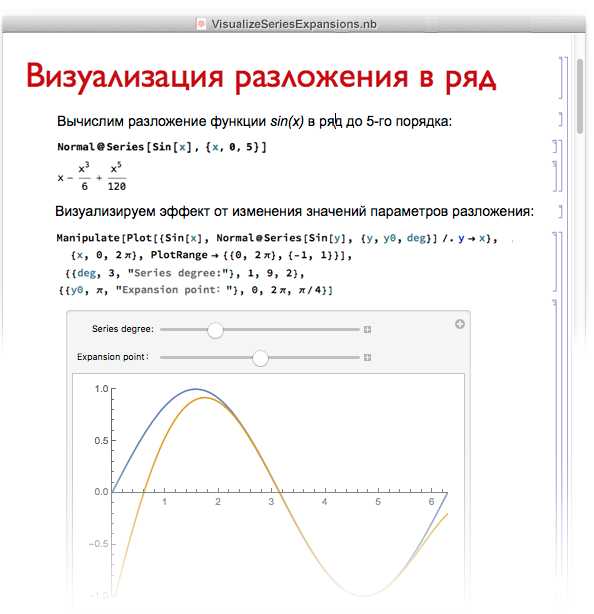
В Wolfram Mathematica для ввода математических выражений используется система, сочетающая как традиционный текстовый ввод, так и визуальный интерфейс. Чтобы записать формулу, можно использовать клавиатуру с синтаксисом Wolfram Language. Например, для степени применяется символ ^: x^2, а для корня – функция Sqrt[x]. Для ввода дробей удобно применять комбинацию клавиш Ctrl + /, которая создает структуру дроби с числителем и знаменателем.
Редактирование формул происходит в динамическом редакторе: при выделении части выражения появляются стрелки для навигации внутри структуры, что позволяет точно вставлять, заменять или удалять элементы. Для быстрого перехода между частями формулы используйте клавиши стрелок или Ctrl + → и Ctrl + ←.
Автоматическое дополнение и подсветка синтаксиса помогают избежать синтаксических ошибок. При вводе функций достаточно начать печатать имя, и система предложит варианты. Для замены оператора достаточно выделить символ и набрать новый. Undo и Redo работают через стандартные Ctrl + Z и Ctrl + Y.
Особое внимание стоит уделить работе с шаблонами и структурированными выражениями, например, списками или матрицами. Их ввод реализован через скобки: фигурные для списков {a, b, c}, двойные квадратные для матриц {{1,2},{3,4}}. Для быстрого добавления элементов используйте автозаполнение и вкладки между элементами.
Для редактирования уже введенных выражений удобен режим выделения и вставки, а также встроенные инструменты преобразования (например, выделить подвыражение и применить Expand или Simplify через контекстное меню или горячие клавиши). Это ускоряет работу и минимизирует количество ошибок.
Использование встроенных функций для вычислений
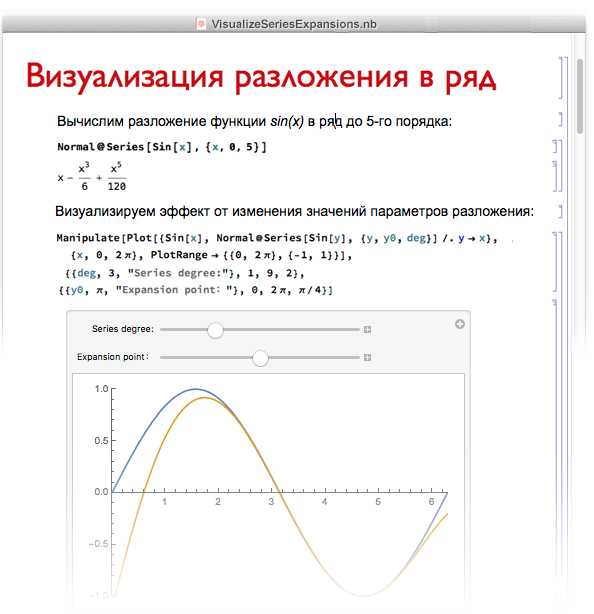
Wolfram Mathematica содержит тысячи встроенных функций, оптимизированных для различных математических операций. Для выполнения вычислений необходимо правильно выбирать функции, учитывая тип задачи и структуру данных.
Для арифметических операций используют базовые функции: Plus (сложение), Times (умножение), Power (возведение в степень). Например, выражение Plus[3, 5] возвращает 8, а Power[2, 3] – 8.
Для работы с аналитическими выражениями применяют функции D (дифференцирование), Integrate (интегрирование), Simplify и FullSimplify для упрощения. Например, D[Sin[x]^2, x] вычисляет производную от Sin[x]^2.
Численные вычисления проводят с помощью N – переводит точные выражения в числовой вид с заданной точностью, например N[Pi, 20] выведет число π с 20 знаками после запятой.
Для работы с матрицами и списками используют функции MatrixForm (отображение), Transpose, Det (определитель), Inverse. К примеру, Det[{{1, 2}, {3, 4}}] вернет -2.
Функции часто комбинируют, используя вложенность: Simplify[D[Integrate[Exp[-x^2], {x, 0, t}], t]] вычисляет производную интеграла по верхнему пределу.
Для получения списка всех функций по теме используйте команду ?Тема*, например ?Integrate*. Это ускоряет выбор подходящей функции.
Рекомендуется внимательно изучать документацию через F1 или команду ?ИмяФункции – там описаны синтаксис, аргументы и примеры. Это позволяет избежать ошибок при сложных вычислениях.
Встроенные функции обрабатывают символические и числовые данные, что делает Mathematica универсальным инструментом для математики и инженерии.
Построение графиков и визуализация данных
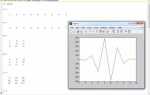
Для построения графиков в Wolfram Mathematica используется функция Plot, позволяющая визуализировать функции одной переменной. Например, Plot[Sin[x], {x, 0, 2 Pi}] отобразит синусоиду на интервале от 0 до 2π. Для функций нескольких переменных применяется Plot3D, например, Plot3D[Sin[x y], {x, 0, Pi}, {y, 0, Pi}].
Для работы с дискретными данными полезна функция ListPlot, которая строит график по набору точек. Можно управлять стилем точек через опции, например, PlotMarkers -> {«●», 12} задаст круглые маркеры размером 12.
Визуализация данных в виде гистограмм реализуется функцией Histogram. Пример: Histogram[data, 20] построит гистограмму с 20 интервалами. Для улучшения читаемости можно добавить опцию ChartStyle -> «Pastel».
Для комбинирования нескольких графиков используют Show. Если требуется сравнить функции, например, Show[Plot[Sin[x], {x, 0, 2 Pi}], Plot[Cos[x], {x, 0, 2 Pi}]] объединит их на одном графике.
Визуальные параметры, такие как цвета, толщины линий и подписи, настраиваются через опции PlotStyle, AxesLabel, PlotLegends. Для добавления легенды используется пакет Legended или встроенная опция PlotLegends -> «Expressions».
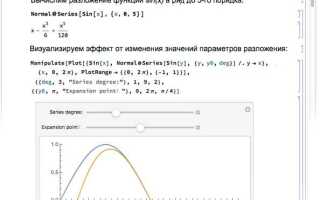
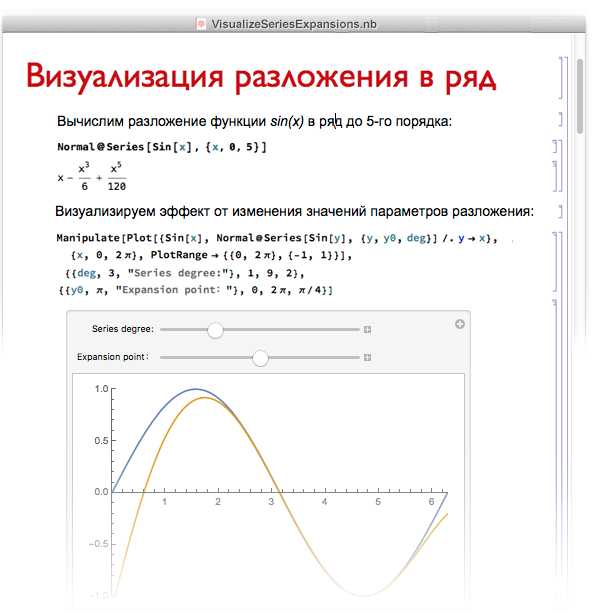
Для интерактивной визуализации применяется функция Manipulate, которая позволяет изменять параметры графика в реальном времени. Пример: Manipulate[Plot[A Sin[x], {x, 0, 2 Pi}], {A, 1, 5}] создает динамическое изменение амплитуды синусоиды.
Обратите внимание, что все функции поддерживают детальную настройку осей через Ticks и GridLines, что помогает улучшить восприятие данных. Для сложных визуализаций доступен широкий набор специализированных функций, например, ContourPlot для изолиний и DensityPlot для цветовых карт.
Работа с переменными и списками данных
Переменная в Wolfram Mathematica присваивается с помощью оператора «=». Для создания и изменения значений достаточно написать, например:
x = 10
Для определения переменной с ленивыми вычислениями используется «:=» (SetDelayed), когда выражение вычисляется при каждом обращении:
y := RandomInteger[{1, 100}]
Списки создаются с помощью фигурных скобок:
list = {1, 2, 3, 4, 5}
Работа со списками включает следующие ключевые операции:
- Доступ к элементам: обращение по индексу через двойные скобки, индексация начинается с 1.
list[[3]]вернёт третий элемент. - Изменение элементов: присваивание по индексу:
list[[2]] = 20заменит второй элемент. - Добавление элементов: с помощью Append:
list = Append[list, 6]добавит элемент в конец. - Удаление элементов: функция Delete:
list = Delete[list, 1]удалит первый элемент. - Фильтрация: Select позволяет выбрать элементы по условию:
Select[list, # > 3 &]вернёт элементы больше 3.
Для итерации по списку удобно использовать функции Map и Table:
Map[f, list]применит функцию f к каждому элементу.Table[i^2, {i, 1, 5}]создаст список квадратов чисел от 1 до 5.
Переменные и списки могут содержать значения любых типов – числа, строки, выражения, функции. Mathematica динамически определяет тип данных.
Рекомендуется использовать описательные имена переменных без пробелов и специальных символов. Для комплексных данных удобно применять вложенные списки или ассоциативные структуры (Association).
Автоматизация задач с помощью скриптов и циклов
В Wolfram Mathematica автоматизация часто строится на использовании циклов и функций для повторения и обработки данных. Основные операторы циклов – For, While и Do – позволяют организовать последовательное выполнение команд, минимизируя ручной ввод.
Для создания скриптов достаточно оформить последовательность команд в едином файле с расширением .wl или .m, который можно запускать в Mathematica. Внутри скрипта применяйте циклы для повторяющихся операций: например, для обработки списка чисел используйте конструкцию Do[выражение, {i, 1, n}], где n – количество повторов.
Цикл For имеет форму For[начало; условие; шаг, тело]. Он удобен, если необходима гибкая настройка изменения счетчика и условий выхода. While повторяет тело до тех пор, пока условие истинно, что подходит для работы с динамическими данными.
Вместо традиционных циклов часто применяют встроенные функции высшего порядка: Map, Table, Fold, которые обеспечивают более компактный и читаемый код. Например, Table[f[i], {i, 1, n}] создаст список значений f[i].
Для автоматической обработки больших объемов данных рекомендуется комбинировать циклы с функциями сохранения результатов в переменные и последующей их обработкой, что позволяет избежать лишних вычислений и ускорить выполнение.
В итоге автоматизация в Mathematica – это грамотное сочетание циклов, функционального программирования и скриптового оформления, что обеспечивает повторяемость, удобство и масштабируемость решения задач.
Экспорт результатов и интеграция с другими программами

Wolfram Mathematica предоставляет несколько мощных способов для экспорта данных и интеграции с внешними приложениями. Основные форматы экспорта включают:
- Данные: CSV, XLSX, JSON, XML – подходят для передачи числовых и табличных данных в Excel, базы данных и веб-приложения.
- Графика: PNG, JPEG, PDF, SVG – для публикации и дальнейшего редактирования в графических редакторах или вёрстке.
- Код: C, Fortran, Python – экспорт вычислительных функций и алгоритмов для использования в других языках программирования.
- Документы: PDF, LaTeX – для подготовки научных отчетов и публикаций с математической разметкой.
Команда для экспорта выглядит так: Export["путь/имя_файла.формат", объект]. Важно указывать правильное расширение файла, соответствующее формату.
Для автоматизации обмена данными можно использовать пакет WSTP (Wolfram Symbolic Transfer Protocol). Он позволяет:
- Создавать двунаправленные каналы связи между Mathematica и другими языками.
- Передавать сложные структуры данных без потерь.
- Встраивать вычисления Mathematica в собственные приложения.
Интеграция с Python особенно популярна: через пакет ExternalEvaluate можно запускать Python-скрипты и передавать данные в обе стороны. Для этого:
- Установите Python и необходимые библиотеки.
- Выполните в Mathematica:
ExternalEvaluate["Python", код]. - Используйте
ExportиImportдля передачи файлов между средами.
Для обмена с Excel удобно использовать формат XLSX с функцией Export. При необходимости считывать или записывать большие таблицы можно применять Import и Export с опциями для определения листов и диапазонов.
При экспорте сложных графиков рекомендуется использовать векторные форматы (SVG, PDF) – они сохраняют масштабируемость и качество. Для презентаций подходит экспорт в PDF с встроенными интерактивными элементами.
Вопрос-ответ:
Как создать и выполнить простейший вычислительный пример в Wolfram Mathematica?
Для создания простейшего вычисления в Wolfram Mathematica достаточно открыть новый блокнот и ввести выражение, например, 2+2, а затем нажать Shift+Enter. Программа автоматически вычислит результат и выведет его под введённой формулой. Такой подход работает для любых арифметических операций, функций и выражений.
Какие типы данных поддерживает Mathematica и как их можно использовать в расчетах?
Mathematica работает с разными типами данных: числами (целыми, рациональными, вещественными), символами, списками, строками, матрицами и даже функциями как объектами. Например, списки применяются для хранения и обработки коллекций данных, а символы позволяют задавать переменные и функции для последующих вычислений. Важно понимать, что Mathematica поддерживает как численные, так и символические вычисления, что расширяет возможности анализа.
Как в Wolfram Mathematica строить графики функций и настраивать их внешний вид?
Для построения графика функции достаточно использовать команду Plot, указывая функцию и диапазон переменной. Например, Plot[Sin[x], {x, 0, 2*Pi}] создаст график синуса на интервале от 0 до 2π. Чтобы изменить цвет, добавить заголовок или оси, можно использовать дополнительные параметры, например, PlotStyle для цвета или AxesLabel для подписей. Также есть множество команд для трехмерной графики и более сложных визуализаций.
Как сохранять и экспортировать результаты работы в Mathematica для дальнейшего использования?
Результаты в Mathematica можно сохранить несколькими способами. Для сохранения всего блокнота используйте меню Файл → Сохранить как, выбрав формат .nb. Для экспорта графиков или таблиц в более универсальные форматы, например, PDF, PNG или CSV, доступны функции Export и меню экспорта. При этом можно указать конкретные настройки качества и формат, что позволяет легко использовать полученные данные в других программах.