Как считать комплексные числа в mathcad

Mathcad предоставляет мощный набор инструментов для работы с комплексными числами, позволяя выполнять как базовые арифметические операции, так и сложные аналитические преобразования. Важно учитывать, что Mathcad автоматически распознает комплексные выражения при использовании стандартного обозначения i или j, что значительно упрощает процесс вычислений.

Для точного вычисления аргумента и модуля комплексного числа в Mathcad применяются встроенные функции abs() и arg(). При этом функция arg() возвращает угол в радианах с учётом знаков действительной и мнимой части, что обеспечивает корректную интерпретацию расположения числа в комплексной плоскости.

Mathcad поддерживает работу с комплексными массивами и векторами, что особенно полезно при решении инженерных задач. Рекомендуется использовать функцию complex() для явного создания комплексных чисел, что помогает избежать ошибок при вводе данных.

Для выполнения операций над комплексными функциями доступны методы численного дифференцирования и интегрирования, позволяющие работать с комплексными аргументами. Совмещение этих методов с графическими возможностями Mathcad обеспечивает удобный анализ результатов.

Ввод и отображение комплексных чисел в Mathcad

В Mathcad комплексные числа вводятся с использованием стандартного обозначения: действительная часть, знак и мнимая часть с символом "i" или "j" (например, 3+4i). Для ввода комплексного числа достаточно набрать выражение в поле ввода и подтвердить Enter.

Для создания комплексных чисел также применяется функция complex(x,y), где x – действительная часть, y – мнимая. Такой подход полезен при формировании чисел из вычисленных компонентов.

Для более удобного анализа можно применить команду rect() для преобразования из полярной формы в алгебраическую, а polar() – для обратного преобразования. Mathcad автоматически интерпретирует комплексные выражения в форму, удобную для дальнейших вычислений и визуализации.

При работе с комплексными массивами и матрицами Mathcad поддерживает ввод элементов в виде комплексных чисел по отдельности или через функцию complex(), сохраняя точность и структуру данных.

Основные арифметические операции с комплексными числами

В Mathcad комплексные числа представлены в форме z = a + bi, где a – действительная часть, b – мнимая. Для выполнения арифметических операций рекомендуется использовать встроенные функции и операторы, обеспечивающие точные вычисления и упрощение выражений.

Сложение и вычитание комплексных чисел в Mathcad выполняется поэлементно: z1 + z2 и z1 - z2. Результат – комплексное число с суммой или разностью действительных и мнимых частей соответственно.

Умножение z1 * z2 реализуется по правилу распределения с учетом свойства i² = -1. Mathcad автоматически обрабатывает эти вычисления, что исключает необходимость ручного раскрытия скобок.

Деление z1 / z2 проводится путем умножения числителя и знаменателя на сопряженное к знаменателю число conj(z2), что переводит знаменатель в действительное число и упрощает выражение. В Mathcad оператор деления комплексных чисел реализован напрямую и корректно обрабатывает эту операцию без дополнительных действий пользователя.

Возведение в степень комплексного числа удобно производить через функцию pow(z, n) или оператор z^n. Для вещественных показателей используется формула z^n = exp(n * ln(z)), где ln(z) – комплексный логарифм, обеспечивающий правильное определение результата.

Для комплексных чисел доступна функция извлечения корней root(z, n), вычисляющая все n комплексных корней с использованием формулы Муавра. Mathcad возвращает все корни в виде массива, что позволяет анализировать все решения задачи.

Рекомендуется использовать встроенные функции Mathcad для вычислений с комплексными числами, поскольку они автоматически учитывают особенности арифметики и минимизируют ошибки, связанные с ручным расчетом.

Вычисление модуля и аргумента комплексного числа

В Mathcad модуль комплексного числа z = x + iy вычисляется с помощью функции abs(z), которая возвращает корень квадратный из суммы квадратов действительной и мнимой частей: |z| = √(x² + y²). При этом переменные x и y можно получить через real(z) и imag(z) соответственно.

Для вычисления аргумента комплексного числа используется функция arg(z), возвращающая угол в радианах в интервале от -π до π. Важно учитывать направление вычисления: arg(z) определяется как arctan(y/x) с учётом знаков x и y, что гарантирует корректное положение аргумента в комплексной плоскости.

Рекомендуется использовать встроенные функции abs и arg без самостоятельного вычисления через формулы, так как Mathcad учитывает особенности числовых методов и предотвращает ошибки при граничных значениях, например, когда x или y равны нулю.

Для удобства визуализации можно вывести значения модуля и аргумента рядом с самим комплексным числом, что облегчает контроль результатов при работе с массивами комплексных данных.

Применение функций комплексного анализа в Mathcad

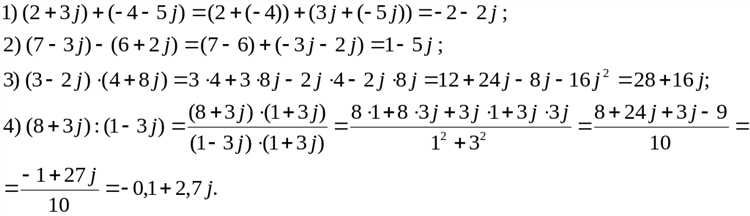
Mathcad предоставляет широкий набор встроенных функций для работы с комплексными числами, что позволяет эффективно решать задачи комплексного анализа без необходимости программирования. Основные возможности включают вычисление комплексных экспонент, логарифмов, тригонометрических и гиперболических функций с комплексным аргументом.

Для анализа комплексных функций в Mathcad важно учитывать следующие рекомендации:

• Использовать встроенную функцию abs() для определения модуля комплексного числа и arg() для вычисления аргумента.
• Для вычисления комплексной экспоненты применять функцию exp(), поддерживающую комплексные аргументы, что позволяет получать значения вида e^(a+bi).
• Логарифмы вычислять через функцию ln(), которая корректно работает с комплексными числами и учитывает ветвь аргумента.
• Для комплексных тригонометрических функций использовать стандартные функции sin(), cos(), tan(), поддерживающие комплексные входные данные.
• Гиперболические функции sinh(), cosh(), tanh() применяются аналогично и позволяют выполнять аналитические преобразования.

При работе с комплексными переменными полезно применять следующие подходы:

1. Разложение функции на вещественную и мнимую части через функции real() и imag() для анализа и визуализации.
2. Использование численных методов интегрирования и дифференцирования, встроенных в Mathcad, для комплексных функций с учетом правильной обработки мнимой части.
3. Построение графиков комплексных функций, в том числе отображение модуля и аргумента, с применением параметрических графиков и цветовых карт.
4. Оптимизация вычислений с помощью векторизации и использования массивов комплексных чисел для пакетной обработки.

Mathcad позволяет интегрировать вычисления комплексного анализа в инженерные и научные задачи, облегчая решение уравнений, исследование аналитических свойств функций и моделирование процессов, связанных с комплексными переменными.

Решение уравнений с комплексными коэффициентами

Mathcad поддерживает решение алгебраических и дифференциальных уравнений с комплексными коэффициентами, используя встроенные функции и численные методы. Для точного результата важно явно указать комплексные переменные и коэффициенты в форме a + b*i, где i – мнимая единица.

При решении линейных уравнений с комплексными коэффициентами применяйте функцию solve или solveBlock, задавая уравнение и переменную для поиска. В случае полиномиальных уравнений используйте root или polyroots, которые возвращают все комплексные корни. Для повышения точности вычислений рекомендуется увеличивать количество знаков в настройках Mathcad, поскольку комплексные корни чувствительны к числовым погрешностям.

В системах уравнений с комплексными коэффициентами применяется аналогичный подход, но с указанием всех уравнений и переменных. В таких случаях полезно использовать комплексные матрицы и функции линейной алгебры, например, inverse и linsolve, учитывая, что матрицы содержат комплексные элементы.

Для дифференциальных уравнений с комплексными коэффициентами Mathcad позволяет задавать комплексные функции и применять встроенные численные решатели, такие как rkfixed или rkadaptive. Важным моментом является корректное определение начальных условий с комплексными значениями и контроль шага интегрирования для предотвращения накопления ошибки.

Обязательно проверяйте результат на корректность с помощью функций abs и arg, чтобы анализировать модуль и аргумент комплексного решения. Это особенно актуально при работе с колебательными системами и сигналами, где комплексные корни определяют амплитуду и фазу.

Построение графиков комплексных функций в Mathcad

Для визуализации комплексных функций в Mathcad требуется разложение функции на действительную и мнимую части. В Mathcad комплексная переменная обычно задаётся как z := x + i·y, где x и y – действительные переменные. Для построения графиков создайте двумерную сетку значений x и y, используя оператор матричного диапазона.

Далее вычислите значение функции f(z) на каждой точке сетки, разделяя результат на действительную часть Re(f(z)) и мнимую Im(f(z)). Для отображения поверхности используйте встроенную функцию 3D-графика Mathcad – surface, где по осям x и y откладываются координаты, а по оси z – значения Re(f(z)) или Im(f(z)).

Для анализа модуля функции применяйте выражение |f(z)| = sqrt(Re(f(z))² + Im(f(z))²). График модуля строится аналогично, что позволяет выявить особенности амплитуды функции.

Если необходимо отобразить аргумент функции, используйте встроенную функцию arg() или вычислите через atan2(Im(f(z)), Re(f(z))). График аргумента помогает визуализировать фазовые изменения и особенности точек разрыва.

В Mathcad удобно комбинировать несколько графиков в одном окне, используя наложение графиков. Это позволяет одновременно просматривать действительную часть, мнимую и модуль функции, улучшая интерпретацию результатов.

Рекомендуется использовать плотность сетки не менее 50×50 для плавности графиков и предотвращения артефактов. Для больших диапазонов переменных стоит применять масштабирование и ограничение области построения, чтобы избежать искажений из-за чрезмерных значений.

При построении графиков комплексных функций важно учитывать особенности вычислений с комплексными аргументами: избегать деления на ноль и правильно обрабатывать особые точки, используя функции Mathcad для проверки условий и обработки исключений.

Вопрос-ответ:

Какие основные способы работы с комплексными числами поддерживаются в Mathcad?

Mathcad позволяет выполнять операции с комплексными числами, используя как алгебраические выражения, так и встроенные функции. Можно задавать комплексные числа в стандартной форме a + bi, а также в полярной форме с помощью модуля и аргумента. Для вычислений доступны функции для нахождения модуля, аргумента, возведения в степень и извлечения корней.

Как в Mathcad задать комплексное число в полярной форме и выполнить преобразование в алгебраическую?

Чтобы задать комплексное число в полярной форме, в Mathcad используют модуль и аргумент: число записывается как r*exp(i*φ), где r — длина вектора, а φ — угол. Для перевода в алгебраическую форму применяют функции cos(φ) и sin(φ): число будет равно r*(cos(φ) + i*sin(φ)). Mathcad позволяет выполнять такие преобразования автоматически с помощью встроенных команд.

Можно ли в Mathcad визуализировать комплексные числа, например, на комплексной плоскости?

Да, Mathcad поддерживает графическое отображение комплексных чисел. Для этого применяются функции построения точек или графиков, где по оси абсцисс откладывается действительная часть, а по оси ординат — мнимая. Это удобно для анализа расположения чисел и понимания их свойств, таких как расстояние и угол относительно начала координат.

Какие функции в Mathcad помогут вычислить степень и корни комплексных чисел?

Для возведения в степень в Mathcad применяют оператор возведения в степень (^), который работает с комплексными числами. Для извлечения корней используют функцию корня с указанием порядка. Также есть функции, работающие через экспоненту и логарифм, позволяющие получать любые степени и корни, включая комплексные значения.

Как в Mathcad можно вычислить аргумент комплексного числа и почему это важно?

Вычисление аргумента (фазы) комплексного числа в Mathcad производится с помощью функции arg(z), где z — заданное комплексное число. Аргумент показывает угол между положительной осью действительных чисел и вектором, соответствующим комплексному числу. Это помогает понять направление и фазу числа, что важно для задач, связанных с анализом сигналов и электрическими цепями.