Работа с экспоненциальными функциями в Mathcad требует точного понимания синтаксиса и механизмов визуализации. Mathcad поддерживает построение графиков функций вида y = a·e^(bx), где a и b – числовые коэффициенты, а e – основание натурального логарифма. Для корректного отображения важно задать диапазон переменной x и определить шаг дискретизации.
Для определения экспоненциальной функции необходимо использовать встроенную константу e или функцию exp(). Например, выражение exp(2·x) будет эквивалентно e^(2·x). Диапазон значений переменной задаётся через оператор двоеточия: x := 0, 0.1 .. 5. Шаг 0.1 обеспечивает достаточную точность при построении гладкой кривой без перегрузки графика.
Построение графика выполняется вставкой компонента График X-Y и указанием имени переменной x на оси абсцисс, а выражения exp(b·x) – на оси ординат. Mathcad автоматически масштабирует оси, но рекомендуется вручную установить границы, чтобы акцентировать ключевые участки роста функции. Использование маркеров и подписи осей улучшает читаемость диаграммы.
При сравнении экспонент с различными коэффициентами удобно использовать множественные кривые на одном графике. Это позволяет визуально оценить влияние параметров a и b на форму графика. Добавление легенды и сетки упрощает анализ, особенно при работе с несколькими функциями одновременно.
Ввод математического выражения для экспоненты
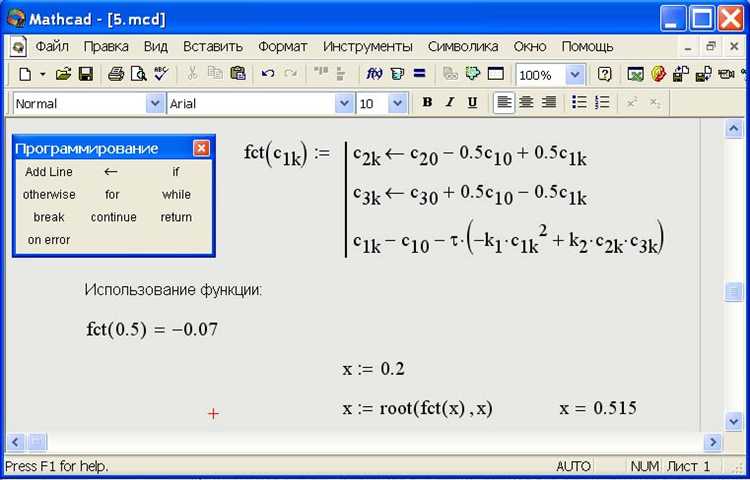
Для ввода экспоненциальной функции в Mathcad используется встроенная функция exp(x), где x – аргумент. Это выражение автоматически интерпретируется как \( e^x \), где \( e \approx 2{,}718 \).
- Чтобы ввести
e^x, просто наберитеexp(x). Mathcad автоматически форматирует результат в виде экспоненты. - Альтернативный способ – использовать клавишу возведения в степень: введите
e, затем нажмите^и укажите степень. Например:e^x. - Для построения выражений вида \( e^{x^2 — 3x + 2} \), заключите весь показатель степени в скобки:
exp(x^2 - 3*x + 2). - Mathcad отличает строчные и прописные символы: вводите
expименно в нижнем регистре. - При использовании переменной в степени, она должна быть определена заранее или иметь числовое значение.
Пример корректного ввода: f(x) := exp(-x^2). После подтверждения клавишей Enter Mathcad распознает выражение как функцию и отобразит результат графически при построении.
Настройка осей и диапазона значений переменной
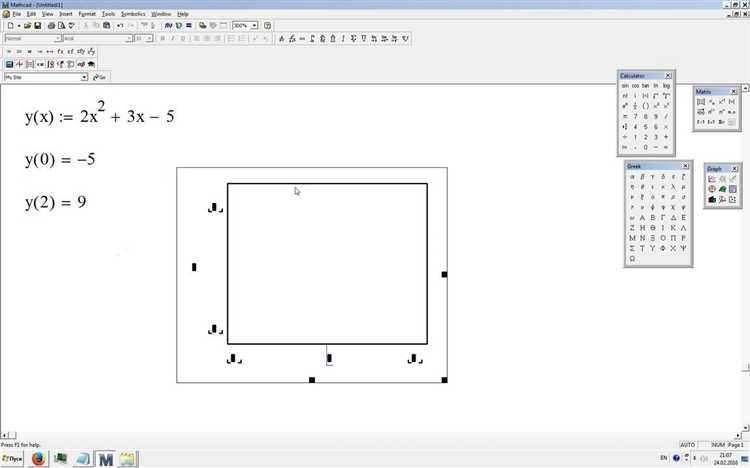
Для корректного построения экспоненциальной функции в Mathcad необходимо точно задать диапазон значений независимой переменной и откорректировать параметры осей графика. Это обеспечит полное отображение характерных особенностей кривой.
Диапазон значений переменной задается через операторы определения: x := старт, шаг..конец. Например, для построения экспоненты e^x в пределах от -2 до 2 с шагом 0.1 используйте запись: x := -2, 0.1..2. Малый шаг позволяет повысить плавность графика, но увеличивает объём вычислений.
Настройка осей осуществляется через двойной щелчок по графику. В открывшемся окне выберите вкладку Axes. Установите минимальное и максимальное значение для осей X и Y вручную. Например, для отображения экспоненты от -2 до 2 логично задать ось X от -2.5 до 2.5, а ось Y от 0 до 10, учитывая быстрое возрастание функции при положительных значениях x.
Рекомендуется отключить автоматическое масштабирование (опция Auto Scale) и задать фиксированный интервал делений (Grid Lines) для удобства анализа. Убедитесь, что ось Y начинается с нуля, чтобы избежать искажений визуального восприятия экспоненты.
Если график отображается частично или искажён, проверьте шаг переменной и масштаб осей. При необходимости уменьшите шаг или увеличьте диапазон значений на осях, особенно по Y.
Использование встроенной функции exp() в Mathcad
Функция exp(x) в Mathcad реализует вычисление экспоненты по основанию e, где x – действительное или комплексное число. Она позволяет быстро получать значения ex без необходимости определения константы e вручную.
Для вызова функции достаточно ввести exp(x) в рабочей области. Mathcad автоматически интерпретирует x как аргумент показательной функции. Если ввести, например, exp(2), результатом будет приблизительно 7.389.
Функция поддерживает векторные и матричные аргументы. При передаче массива значений результатом будет массив, в котором к каждому элементу применена экспонента. Это удобно при работе с массивами данных, моделировании процессов роста или затухания.
В комплексной области exp() корректно обрабатывает аргументы вида a + bi, возвращая значение по формуле Эйлера. Пример: exp(π·i) возвращает приблизительно −1, что соответствует тождеству Эйлера.
Для построения графиков используйте exp(x) как часть выражения в функции от переменной x. Например, определив f(x) := exp(−x²), можно визуализировать гауссову кривую через встроенные инструменты построения графиков.
Чтобы повысить точность расчетов, убедитесь, что формат отображения результатов настроен на достаточное количество значащих цифр. Это критично при работе с малыми или большими значениями экспоненты, где округление может исказить результат.
Построение графика экспоненты с помощью вставки графика
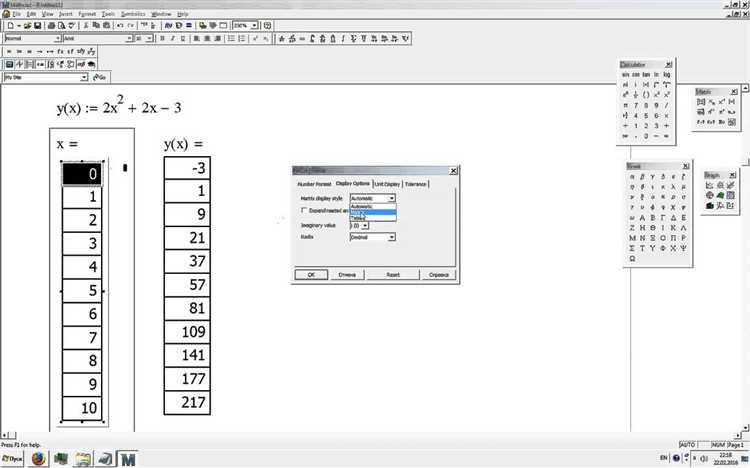
Для визуализации экспоненциальной функции в Mathcad используется элемент вставки графика. Начните с определения переменной аргумента, например: x := 0, 0.1 .. 10. Это задаёт диапазон значений от 0 до 10 с шагом 0.1.
Далее определите функцию: y(x) := exp(x). Mathcad автоматически интерпретирует exp(x) как ex, где e – основание натурального логарифма.
Для построения графика выберите на панели инструментов элемент 2D-график и щёлкните в рабочей области. В появившемся окне введите x в нижнем поле (ось X), а в верхнем – y(x) (ось Y). Mathcad мгновенно отобразит график экспоненты.
Для точной настройки используйте панель форматирования графика. Здесь можно задать масштаб осей, сетку, цвет линии, тип маркеров. Установите, например, логарифмическую шкалу по оси Y для лучшей наглядности при больших значениях x.
Если необходимо сравнение с другими функциями, добавьте дополнительные выражения в верхнюю часть графика, например: exp(0.5·x) или exp(-x). Все кривые будут отображаться одновременно, что удобно для анализа.
Не забудьте подписать оси и задать название графика через контекстное меню – это упрощает чтение графика и интерпретацию данных при подготовке отчётов или презентаций.
Сравнение экспоненциальной функции с другими функциями на одном графике
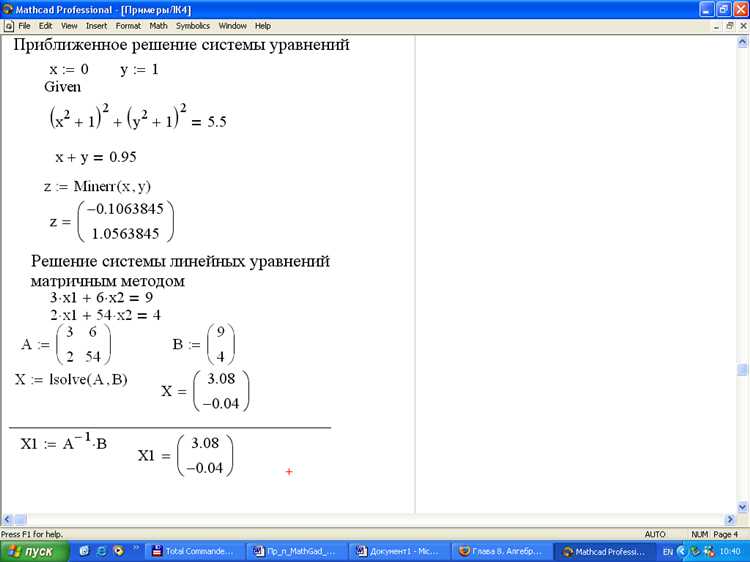
Для анализа отличий поведения экспоненты в Mathcad рекомендуется построить на одном графике функции: экспоненциальную \( y = e^x \), линейную \( y = x \), квадратичную \( y = x^2 \) и логарифмическую \( y = \ln(x) \). В диапазоне \( x \in [0, 5] \) экспонента резко выделяется по скорости роста, начиная с медленного увеличения и стремительно обгоняя все остальные функции после \( x \approx 2 \).
В Mathcad задать все функции можно через векторы значений x и соответствующие выражения для y. Например:
\[
x := 0, 0.1 .. 5 \\
y_{exp} := e^x \\
y_{lin} := x \\
y_{quad} := x^2 \\
y_{log} := \ln(x)
\]
Для построения графика используйте компонент 2D Graph. Отметьте все функции на одном поле и различайте их по цвету. Обязательно установите одинаковый масштаб по осям, чтобы визуально не исказить сравнение.
Особое внимание следует уделить поворотной точке \( x \approx 4.8 \), где \( e^x \approx x^2 \), что хорошо демонстрирует ускорение роста экспоненты. Также важно, что логарифмическая функция существенно отстает и практически «выравнивается» в верхней части графика, несмотря на неограниченность роста.
Ошибки при построении экспоненты и способы их устранения
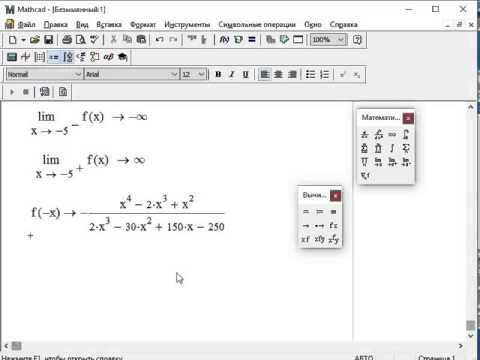
Для корректного построения экспоненты необходимо использовать функцию exp(x). Это гарантирует правильное вычисление при любом значении переменной и исключает ошибки округления.
Ещё одна частая проблема связана с диапазоном аргумента. При больших значениях x экспонента растёт очень быстро, что может вызвать переполнение или искажение графика. Для визуализации таких данных рекомендуется ограничивать область построения значениями, при которых exp(x) остаётся в пределах машинного представления чисел Mathcad. Альтернативно, стоит использовать логарифмическую шкалу по оси Y, если это допустимо.
Неверное определение переменных также приводит к ошибкам. В Mathcad необходимо убедиться, что переменная x задана как числовой массив или скаляр, а не строка или неопределённый символ. Для построения графика экспоненты нужно использовать диапазон значений, созданный через оператор диапазона, например, x := 0, 0.1..5. Ошибка возникает при попытке использовать неинициализированные или несовместимые с вычислениями значения.
Если график построен, но отображается с артефактами или недостаточной точностью, следует увеличить плотность вычислительных точек. Это делается уменьшением шага в диапазоне переменной. Например, вместо 0, 1..5 использовать 0, 0.01..5. Это устраняет «ступенчатость» и делает кривую гладкой.
При вычислении экспоненты с комплексными аргументами обязательна проверка правильности задания комплексной части. В Mathcad комплексные числа вводятся через оператор i. Ошибка возникает, если использовать j или неопределённые обозначения. Например, корректно: exp(i * pi), некорректно: exp(j * pi).
Для устранения большинства ошибок рекомендуется использовать встроенную справку Mathcad и проверять шаги вычислений с помощью встроенных инструментов отладки, таких как просмотр значений переменных и тестовые вычисления отдельных выражений.
Вопрос-ответ:
Как в Mathcad можно построить график функции экспоненты?
Для построения графика экспоненты в Mathcad необходимо задать функцию вида y = exp(x). Затем создайте вектор значений переменной x на нужном интервале, например, от -2 до 2 с небольшим шагом. После этого выберите инструмент построения графика и укажите в качестве осей значения x и соответствующие значения y = exp(x). В результате появится график, отражающий рост функции экспоненты.
Можно ли в Mathcad использовать экспоненту для комплексных чисел и как это сделать?
Да, Mathcad поддерживает вычисления с комплексными числами, включая функцию экспоненты. Чтобы построить экспоненту комплексного аргумента, задайте переменную x как комплексное число, например x := 1 + 2i. После этого функция exp(x) рассчитает значение экспоненты с комплексным аргументом. Для визуализации можно построить два графика — по действительной и мнимой части, или использовать трехмерный график с координатами (Re(x), Im(x), |exp(x)|).
Какие параметры можно настраивать при построении графика экспоненты в Mathcad?
При построении графика экспоненты можно изменить диапазон значений переменной x, шаг дискретизации, а также оформить оси — задать подписи и шкалу. В Mathcad доступна настройка цвета и толщины линии графика, добавление сетки, а также выбор типа графика (линейный, точечный и др.). Кроме того, можно добавить заголовок и легенду для лучшей читаемости.
Как вычислить экспоненту сложного выражения в Mathcad и использовать результат в дальнейшем?
В Mathcad можно вводить сложные выражения внутрь функции exp(). Например, exp(a + b*x), где a и b — константы, x — переменная. Результат вычисления можно сохранить в новую переменную, что позволит использовать его в последующих вычислениях. Благодаря встроенным функциям Mathcad автоматически обновит значения при изменении исходных параметров, что облегчает анализ и моделирование.
Почему график экспоненты в Mathcad может выглядеть странно или не отображаться корректно?
Основные причины некорректного отображения связаны с неверно заданным диапазоном переменной x или слишком крупным шагом. Если шаг слишком большой, график будет прерывистым и искажённым. Также возможно, что функция не была правильно определена или переменная не инициализирована. Проверьте правильность ввода функции, диапазона и параметров графика — чаще всего это решает проблему.
Как в Mathcad построить график функции экспоненты с произвольным основанием?
В Mathcad для построения графика экспоненты с произвольным основанием можно задать функцию в виде \(f(x) = a^x\), где \(a\) — любое положительное число. Для этого достаточно ввести выражение с использованием оператора возведения в степень. Затем нужно создать график, выбрав ось X и функцию \(f(x)\). Например, если основание равно 3, то функция будет \(f(x) := 3^x\). Далее, на графике можно задать диапазон значений x для построения кривой.