Какие типы графиков представлены в mathcad

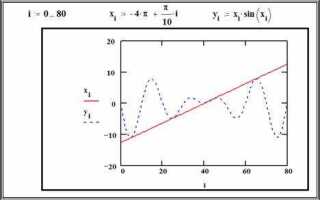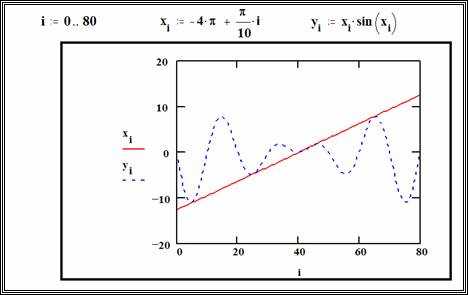
Mathcad предоставляет широкий набор инструментов для визуализации данных, включая различные типы графиков. Эти графики позволяют эффективно представлять и анализировать результаты вычислений, что делает Mathcad незаменимым инструментом для инженеров, ученых и аналитиков. Важно понимать, какие типы графиков доступны, а также когда и как их лучше использовать для получения максимальной пользы.

Основные типы графиков в Mathcad включают графики функций, гистограммы, диаграммы рассеяния и графики векторных полей. Каждый тип графика имеет свои особенности и области применения. Например, графики функций идеально подходят для отображения зависимостей между переменными. Они часто используются для анализа математических моделей или в качестве наглядных примеров решения уравнений. Важно помнить, что для отображения гладких и непрерывных функций следует использовать линии, а для дискретных данных – маркеры.

Для анализа распределений данных и сравнения различных выборок лучше всего использовать гистограммы. Эти графики полезны в статистических исследованиях, где требуется наглядно представить частотное распределение. При этом важно правильно выбрать размер интервала, чтобы избежать слишком сглаженной или, наоборот, разрозненной картины.

Диаграммы рассеяния незаменимы, когда необходимо исследовать корреляцию между двумя переменными. Этот тип графика помогает визуализировать, как изменения одной переменной влияют на другую, что важно для анализа экспериментальных данных или прогнозирования.

Для визуализации полей векторных величин в Mathcad используют графики векторных полей, которые позволяют представлять направления и величины вектора в различных точках пространства. Эти графики особенно полезны в области физики, например, для отображения электрических или магнитных полей.

Выбор типа графика в Mathcad зависит от цели анализа и природы данных. Важно правильно настроить параметры графика, такие как масштабирование и цветовую палитру, чтобы избежать неправильных интерпретаций. Правильный выбор и настройка графика позволяет существенно повысить качество анализа и ускорить принятие решений.

Графики для визуализации функций и их особенности

Графики 2D в Mathcad обычно используются для визуализации одно- и двухпеременных функций. Наиболее распространенным типом является график, отображающий зависимость между независимой и зависимой переменной, например, линейная или экспоненциальная функция. Эти графики просты в интерпретации и идеально подходят для анализа изменений функции по одной переменной. Важной особенностью является возможность точной настройки масштаба осей и цветового оформления, что повышает читабельность при работе с большими объемами данных.

Графики 3D позволяют отображать функции с двумя независимыми переменными. В отличие от 2D-графиков, где оси X и Y отображают изменения, в 3D-графиках ось Z представляет собой результат вычислений для комбинации значений двух переменных. Эти графики полезны для отображения сложных поверхностей, таких как гиперболические или параболические поверхности. В Mathcad можно изменять угол обзора, что помогает лучше понять структуру графика и выявить важные детали.

Для визуализации функций, зависимых от нескольких переменных, особенно в случае сложных зависимостей, часто используют графики контуров или уровней. Такой график отображает линии, по которым функция принимает одинаковые значения. Это позволяет легко анализировать поведение функции на определенных уровнях, например, для оптимизационных задач, где важно определить области максимума или минимума.

Еще одним вариантом являются графики, сочетающие 2D и 3D элементы. В таких графиках можно отобразить линии или кривые, наложенные на 3D-сцену, что позволяет глубже проанализировать данные. Например, для визуализации данных, полученных в процессе многомерного анализа, часто используются комбинации графиков, где функции разных переменных отображаются одновременно.

Важно помнить, что каждый тип графика следует выбирать в зависимости от задачи. Например, для анализа тенденций и поведения функции лучше использовать 2D-графики, в то время как для изучения более сложных взаимозависимостей, где важен анализ нескольких переменных, стоит использовать 3D-графики и графики уровней. В Mathcad легко настроить внешний вид графика, подобрать нужные параметры и стили, что делает анализ данных более точным и наглядным.

Как построить график данных в Mathcad: пошаговая инструкция

1. Откройте Mathcad и создайте новый документ.

2. Введите данные. Для этого создайте в документе переменные, которые будут хранить значения. Например, для набора значений X и Y используйте следующее:

X := 0, 1, 2, 3, 4, 5

Y := 0, 2, 4, 6, 8, 10

3. Выделите область с данными, которые будут использованы для построения графика.

4. Вставьте график. Для этого нажмите на пустое место в документе и выберите команду для вставки графика. В Mathcad это можно сделать через меню «Вставка» -> «График».

5. В настройках графика выберите тип графика, например, «Точка с соединением» или «Линейный график».

6. Укажите, какие переменные должны быть отображены на осях графика. В поле «X» укажите переменную X, в поле «Y» – переменную Y.

7. Настройте внешний вид графика. В разделе «Свойства графика» можно выбрать цвет, стиль линий, добавить подписи к осям и титул. Чтобы добавить подпись, используйте опцию «Добавить текст» и укажите соответствующие метки осей.

8. График автоматически обновится при изменении данных. Для изменения диапазона или добавления новых значений достаточно изменить список данных в переменных X и Y.

9. После завершения настройки графика сохраните документ. Чтобы сохранить график отдельно, можно экспортировать его в формат изображения через меню «Файл» -> «Экспортировать».

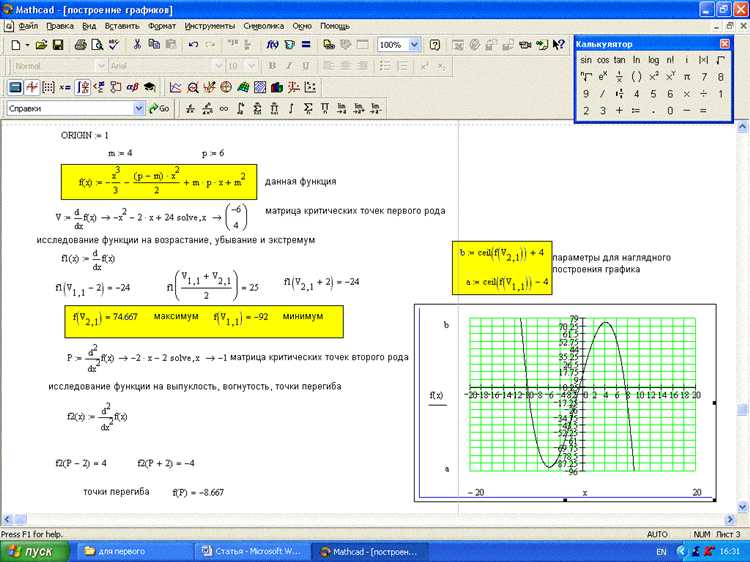
Использование 3D-графиков для анализа многомерных зависимостей

3D-графики в Mathcad позволяют визуализировать сложные многомерные зависимости, которые невозможно представить с помощью стандартных 2D-графиков. Такие графики особенно полезны при анализе данных, где важны взаимосвязи между тремя или более переменными. Применение 3D-графиков открывает возможности для анализа поведения функций в многомерных пространствах, что помогает лучше понять динамику процессов, например, в инженерных расчетах или в анализе экспериментальных данных.

Для создания 3D-графиков в Mathcad используют функции типа «plot3d» или «meshplot», которые отображают зависимости между переменными по осям X, Y и Z. Ключевым моментом является выбор типа графика в зависимости от задачи: линии и точки, поверхности, контуры и т.д. Например, для исследования поверхностей, задаваемых функциями вида Z = f(X, Y), чаще всего применяют графики типа «mesh» или «surface», которые дают четкую картину распределения значений по всей поверхности.

При построении 3D-графиков важно учитывать не только структуру данных, но и точность вычислений. Если данные содержат шум или выбросы, это может повлиять на внешний вид графика и затруднить анализ. Для минимизации таких эффектов можно применять методы сглаживания или фильтрации данных. Также стоит учитывать влияние разрешения графика на производительность системы, так как слишком высокое разрешение может замедлить рендеринг.

В некоторых случаях 3D-графики используются для моделирования процессов, где требуется анализировать зависимость нескольких параметров одновременно, например, в термодинамике или механике. Использование интерактивных графиков в Mathcad позволяет пользователю изменять значения переменных в реальном времени, что значительно ускоряет процесс поиска оптимальных решений и анализа.

Особенно полезно сочетание 3D-графиков с аналитическими инструментами Mathcad, такими как дифференцирование и интегрирование, что позволяет проводить не только визуальный, но и количественный анализ данных. Например, нахождение точек максимума и минимума функции на поверхности может быть выполнено с помощью встроенных инструментов для численного анализа.

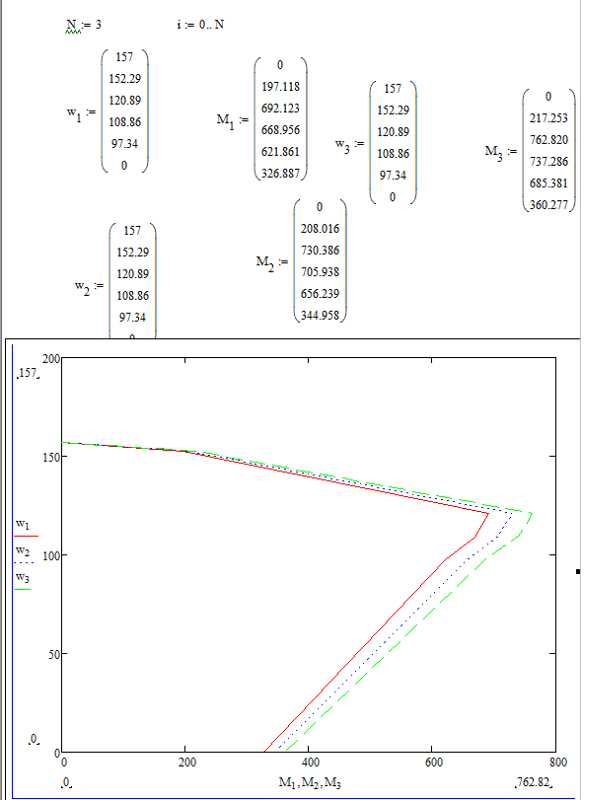
Графики с несколькими осями: когда и как их применять

Графики с несколькими осями в Mathcad позволяют одновременно отображать данные с различными единицами измерения или масштабами, что особенно полезно при анализе взаимосвязанных величин, имеющих сильно отличающиеся величины. Эти графики могут содержать две или более оси, каждая из которых отвечает за свой набор данных.

Типичный случай применения графиков с несколькими осями – это сравнение данных с разными шкалами. Например, при анализе температурных колебаний и давления в одном процессе, где температура изменяется в пределах нескольких сотен градусов, а давление – в пределах нескольких атмосфер.

Когда использовать графики с несколькими осями:

• При сравнении величин с разными единицами измерения. Например, давление в атмосферах и температура в Кельвинах.
• Когда данные сильно отличаются по величине. Если одна величина варьируется от 0 до 1000, а другая от 0 до 1, то для наглядности нужно использовать разные масштабы осей.
• При анализе многокомпонентных процессов. Например, в системах управления или химических реакциях, где несколько факторов влияют друг на друга в разные моменты времени.

Как правильно строить графики с несколькими осями:

1. Выбор оси для каждой переменной. Каждую ось нужно назначить для конкретной переменной, исходя из её масштаба. Например, для данных с величинами порядка тысяч используется правая ось, для более мелких величин – левая.
2. Подписывание осей. Каждая ось должна быть чётко подписана, указывая, какие именно данные она отображает, и их единицы измерения. Это исключит путаницу при интерпретации графика.
3. Правильный выбор типов графиков. Использование линейных или столбчатых графиков для данных с несколькими осями требует внимательного выбора типа линии и маркеров, чтобы различия между данными оставались ясными.
4. Управление масштабом. Важно контролировать шкалу каждой оси, чтобы данные не были искажены. Например, при использовании двух осей с сильно различными величинами можно настроить отображение так, чтобы на обеих осях данные оставались читабельными.

Преимущества и недостатки:

• Преимущества: Графики с несколькими осями позволяют компактно отображать взаимосвязанные данные, улучшая восприятие информации и позволяя проводить комплексный анализ.
• Недостатки: Если график перегружен слишком большим количеством данных, это может затруднить его восприятие. Также следует избегать использования слишком множества осей, так как это может запутать пользователя.

Важным аспектом является обеспечение корректности отображения и совместимости данных, чтобы не возникало ошибок в интерпретации результатов. Например, при наличии очень маленьких и очень больших значений, может потребоваться использование логарифмических шкал для улучшения наглядности.

Диаграммы рассеяния: подходы к работе с экспериментальными данными

1. Подготовка данных

2. Выбор типа маркера

В Mathcad можно настроить внешний вид маркеров на графике: форму, размер, цвет. Выбор маркера должен соответствовать задачам исследования. Например, для отображения крупных наборов данных с возможностью различить группы точек можно использовать разные цвета или формы маркеров. Это упрощает восприятие информации, особенно если экспериментальные данные разделяются на несколько категорий.

3. Масштабирование осей

Один из важнейших аспектов работы с диаграммами рассеяния – правильный выбор масштаба осей. Линейный масштаб подходит для данных, которые изменяются в пределах одной и той же величины, но если данные охватывают широкий диапазон значений, лучше использовать логарифмический масштаб. Это поможет более чётко визуализировать отношения между переменными и выявить скрытые закономерности.

4. Регрессия и трендовые линии

Для анализа связи между переменными на диаграмме рассеяния часто используют линии регрессии. Mathcad предлагает несколько типов регрессионных моделей: линейную, полиномиальную, экспоненциальную и другие. Важно не только построить линию регрессии, но и оценить её точность с помощью коэффициента корреляции или стандартной ошибки.

5. Интерпретация данных

При анализе диаграмм рассеяния важно учитывать не только вид связи между переменными, но и возможные аномалии. Например, если точки на графике сгруппированы в несколько кластеров, это может свидетельствовать о наличии нескольких факторов, влияющих на экспериментальные данные. В таких случаях необходимо провести дополнительный анализ для выявления причин разброса данных.

6. Работа с большими объёмами данных

При работе с большими наборами экспериментальных данных важно правильно организовать отображение точек на диаграмме. Один из способов уменьшить нагрузку на график – использование плотности точек. Для этого можно применить прозрачность маркеров, что позволит легче увидеть зоны концентрации данных без перегрузки графика.

Подходы, описанные выше, помогут эффективно работать с экспериментальными данными в Mathcad, получая точные и информативные визуализации для дальнейшего анализа и принятия решений.

Как работать с графиками ошибок и их роль в аналитике

Графики ошибок в Mathcad предоставляют важную информацию о неопределенностях и точности данных, а также позволяют визуализировать разброс значений. Эти графики полезны для анализа погрешностей, уточнения модели и оценки влияния изменений в данных на результаты расчетов.

Для создания графика ошибок в Mathcad можно использовать несколько типов графиков, например, линейные графики с добавлением вертикальных и горизонтальных линий ошибок или графики с полосами ошибок. Работа с такими графиками требует учета нескольких ключевых аспектов:

• Подготовка данных: Перед созданием графика необходимо точно определить диапазон значений погрешности. Ошибки могут быть абсолютными или относительными, и важно точно понять, как они будут отображаться на графике.
• Типы ошибок: В зависимости от типа эксперимента или модели могут использоваться разные виды ошибок. Абсолютные ошибки показывают разницу между измеренным значением и истинным значением, а относительные ошибки позволяют оценить величину отклонений по отношению к самим данным.
• Добавление ошибок на график: Для точности отображения ошибок в Mathcad используется специальная функция «Error Bars», где можно задать диапазон погрешностей для каждого из значений. Графики могут отображать ошибку как полосы, простирающиеся вверх и вниз от точки данных.

Роль графиков ошибок в аналитике заключается в том, что они дают четкое представление о надежности и точности данных. Они помогают:

• Оценить, насколько данные соответствуют ожидаемым результатам.
• Понять, насколько значимы отклонения в расчетах.
• Проанализировать влияние изменений в исходных данных на результаты модели или эксперимента.
• Определить, какие данные имеют наибольшие погрешности, и решить, нужно ли их улучшать или исключать.

Использование графиков ошибок также важно для моделирования и проверки устойчивости расчетных моделей. Например, если модель показывает значительные отклонения на основе малых изменений данных, это может сигнализировать о необходимости улучшения самого метода расчетов или алгоритма.

Кроме того, работа с графиками ошибок помогает в наглядной демонстрации качества результатов. Например, на графике с малым разбросом ошибок можно утверждать, что модель или эксперимент имеют высокую точность, в то время как большие ошибки указывают на необходимость пересмотра данных или метода обработки.

Интерактивные графики в Mathcad: создание и использование

В Mathcad интерактивные графики позволяют пользователю визуализировать данные в реальном времени и изменять параметры отображаемых функций без необходимости перерисовывать график. Это особенно полезно при анализе зависимостей между переменными, когда нужно быстро увидеть изменения в графике при изменении значений параметров.

Для создания интерактивного графика в Mathcad необходимо использовать инструмент График, который поддерживает функции с возможностью изменения значений через слайдеры или вводные поля. Важно, что Mathcad позволяет привязывать параметры функции к этим элементам управления, что дает пользователю возможность изменять значения и сразу видеть, как это влияет на график.

Процесс создания интерактивного графика начинается с добавления функции на рабочее пространство. После этого, нужно выбрать нужную область графика, где будут отображаться переменные, и установить слайдеры или вводные поля, которые будут управлять значениями этих переменных. Например, можно создать слайдер для изменения параметра функции, который в реальном времени будет изменять внешний вид графика.

Когда слайдер или вводное поле подключено, необходимо установить диапазон значений и шаг изменения, чтобы пользователь мог с удобством изменять параметры. Это сделает график гибким и удобным для анализа. Например, если это график зависимости скорости от времени, пользователь может изменять время с помощью слайдера и сразу видеть, как изменяется скорость.

Рекомендации:

• Для повышения удобства работы с графиками используйте несколько слайдеров для управления несколькими переменными одновременно.
• Определяйте логичные диапазоны значений для каждого слайдера, чтобы не создать график с нелогичными или несуществующими значениями.
• Обратите внимание на выбор типа графика: для многих задач лучше использовать 2D-графики, но для отображения более сложных зависимостей можно применить 3D-графики, которые тоже могут быть интерактивными.
• Используйте цветовые схемы для улучшения восприятия графика, особенно если в нем несколько переменных или осей.

Интерактивные графики могут также быть полезны для презентаций и отчетов, где нужно динамично продемонстрировать изменения данных в зависимости от параметров. Это особенно важно при необходимости показать, как различные факторы влияют на результаты модели или эксперимента.

Наконец, Mathcad позволяет сохранять эти графики с сохранением всех интерактивных элементов, что дает возможность дальнейшего использования в других проектах или демонстрации работы с изменяющимися данными.

Вопрос-ответ:

Какие типы графиков можно создавать в Mathcad?

В Mathcad можно строить различные типы графиков, включая линейные, точечные, графики с несколькими осями, а также комбинированные графики, которые объединяют несколько типов отображения данных. Программа позволяет создавать 2D и 3D графики, например, для отображения функции с несколькими переменными. Также доступны графики для статистических данных, такие как гистограммы или диаграммы рассеяния.

Как в Mathcad построить график функции с несколькими переменными?

Для построения графика функции с несколькими переменными в Mathcad нужно использовать команды для трехмерных графиков. Например, можно построить график функции z=f(x,y)z = f(x, y)z=f(x,y), задав массивы значений для переменных xxx и yyy, а затем используя команду для 3D-графика. В Mathcad есть возможность выбирать различные типы представления, такие как поверхности или контурные линии, чтобы лучше визуализировать зависимости между переменными.

Как сделать график с несколькими осями в Mathcad?

Для того чтобы создать график с несколькими осями в Mathcad, нужно использовать функцию «Add Graph». В процессе построения графика можно добавить дополнительные оси, что позволяет отображать различные наборы данных на одном графике. Каждую ось можно настроить индивидуально по масштабу, цвету и меткам. Это особенно полезно, когда нужно сравнивать несколько разных функций или данных на одном графике с разными масштабами осей.

Как настроить стиль графика в Mathcad, например, изменить цвет линий или точек?

В Mathcad можно настроить внешний вид графика, изменяя свойства линий и точек. Для этого достаточно кликнуть на элемент графика, например, на линию или точку, и выбрать соответствующую команду для изменения цвета, толщины линии или стиля маркера. Также можно выбрать цвет фона графика или изменить другие визуальные параметры, чтобы график лучше соответствовал вашим предпочтениям.

Можно ли в Mathcad строить динамические графики, которые изменяются при изменении данных?

Да, Mathcad поддерживает создание динамических графиков. Это позволяет обновлять график в реальном времени, когда меняются исходные данные. Для этого можно использовать переменные, которые автоматически пересчитываются при изменении значений. Это удобно, например, для визуализации данных, которые зависят от времени или других переменных, и позволяет быстро увидеть, как изменения влияют на график.