Какие уравнения называются матричными в mathcad

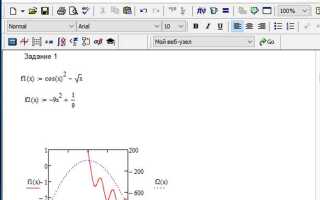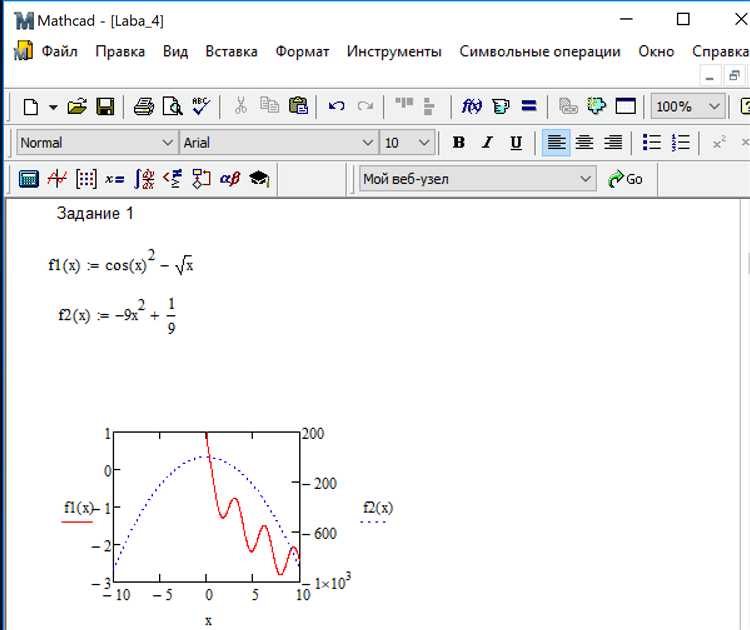
Mathcad предоставляет мощный инструмент для работы с матричными уравнениями, что делает его незаменимым в инженерных расчетах, научных исследованиях и математическом моделировании. Одной из особенностей Mathcad является возможность интеграции математических операций с визуальными и текстовыми данными, что облегчает восприятие сложных решений и повышает эффективность работы. Матричные уравнения в Mathcad могут быть решены с использованием различных методов, в том числе численных и аналитических, что дает широкий спектр возможностей для решения задач в реальном времени.

При решении матричных уравнений в Mathcad важно учитывать возможности работы с многомерными массивами, что позволяет представлять данные в виде матриц и векторах. Это особенно полезно при моделировании систем, где необходимо учитывать взаимозависимость множества параметров. Встроенные функции, такие как inv(), det(), и linsolve(), позволяют легко находить обратные матрицы, вычислять детерминанты и решать системы линейных уравнений, что значительно сокращает время расчетов.

Для решения матричных уравнений в Mathcad особое внимание следует уделить правильному выбору метода решения, поскольку эффективность может существенно различаться в зависимости от типа задачи. Например, при работе с большими матрицами или при необходимости решения уравнений с большим числом переменных предпочтительнее использовать численные методы, такие как метод Гаусса или LU-разложение, которые обеспечивают стабильность и скорость расчетов. В свою очередь, для задач с более низкой размерностью может быть целесообразно использовать аналитические методы для получения точных решений.

Важной особенностью работы с матричными уравнениями в Mathcad является удобная визуализация результатов. Программы позволяют не только отображать решения в числовом виде, но и строить графики, что позволяет наглядно представлять зависимость между различными переменными и оценивать точность моделей. Для инженеров и ученых это открывает дополнительные возможности для анализа и оптимизации процессов в реальном времени.

Матричные уравнения в Mathcad: особенности и применение

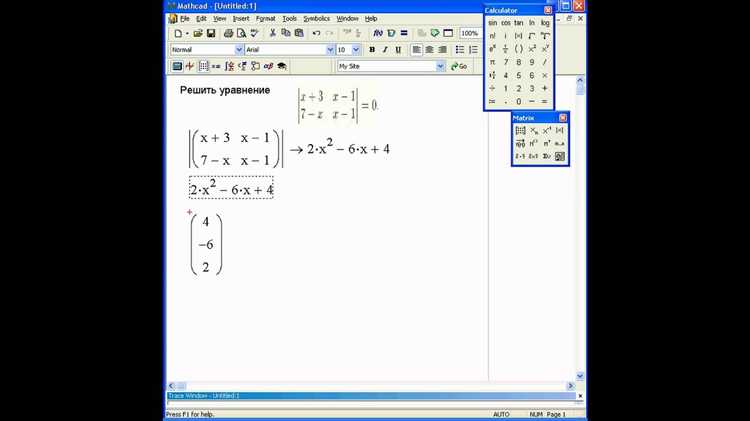
Mathcad предоставляет мощные инструменты для работы с матричными уравнениями, позволяя пользователям решать задачи, которые включают системы линейных уравнений, операции над матрицами и вычисления, связанные с большими данными. В отличие от традиционных математических пакетов, Mathcad отличается интерактивной средой и возможностью визуализации решений.

Одной из ключевых особенностей Mathcad является удобство работы с матричными уравнениями без необходимости заранее вводить сложный синтаксис. Рассмотрим основные аспекты использования матриц и матричных уравнений в Mathcad.

Основные операции с матрицами

• Создание матрицы: Матрицы в Mathcad могут быть заданы вручную через ввод значений в формате строк и столбцов или автоматически с помощью генераторов последовательностей.
• Операции над матрицами: Mathcad поддерживает основные операции, такие как сложение, вычитание, умножение, деление, транспонирование и нахождение обратной матрицы. Эти операции выполняются с использованием стандартных математических символов и команд.
• Решение систем линейных уравнений: Решение систем линейных уравнений через матрицы происходит с использованием оператора “\” для прямого решения или с помощью функций, таких как linsolve для более сложных случаев.

Решение матричных уравнений

Решение матричных уравнений в Mathcad производится с помощью матричных операций и функций. Например, для решения уравнений вида AX = B необходимо воспользоваться операцией умножения матриц и нахождением обратной матрицы. Стандартное решение будет выглядеть так:

• Создайте матрицы A и B.
• Найдите обратную матрицу для A с помощью команды A^(-1).
• Умножьте обратную матрицу на B, чтобы найти решение X = A^(-1) * B.

Mathcad автоматически учитывает размерности матриц, проверяя корректность операций и предотвращая ошибки при несовпадении размеров.

Особенности использования Mathcad для матричных уравнений

• Интерактивность: Mathcad позволяет мгновенно видеть результаты вычислений, что полезно для отладки и анализа решений.
• Визуализация: Возможность построения графиков и диаграмм на основе матричных данных упрощает восприятие результатов и их интерпретацию.
• Поддержка пользовательских функций: Mathcad дает возможность создавать собственные функции для решения специфических задач, включая матричные уравнения, что повышает гибкость инструмента.

Применение в реальных задачах

Матричные уравнения в Mathcad широко применяются в инженерных расчетах, экономических моделях, обработке сигналов и других областях. Например:

• Моделирование динамических систем: В задачи, связанные с управлением системами или анализом вибраций, часто включают матричные уравнения для нахождения откликов системы на различные воздействия.
• Финансовые модели: В экономике матричные уравнения используются для анализа взаимосвязей между различными переменными, например, для решения задач оптимизации портфелей или анализа кредитных рисков.
• Обработка изображений: В задачах обработки изображений матричные уравнения могут использоваться для преобразования данных, например, при фильтрации изображений или вычислении основных компонент в алгоритмах сжатия.

Mathcad значительно упрощает эти процессы благодаря возможности визуализировать решения и следить за промежуточными вычислениями.

Заключение

Использование матричных уравнений в Mathcad эффективно решает задачи в различных областях науки и техники. Благодаря простоте работы с матрицами, интуитивному интерфейсу и мощным вычислительным возможностям, Mathcad остается важным инструментом для инженерных и научных расчетов, позволяя решать сложные матричные уравнения с высокой точностью и быстротой.

Решение линейных матричных уравнений с использованием Mathcad

Применение функции \(\texttt{linsolve}(A, B)\) требует от пользователя объявления исходных матриц \(A\) и \(B\) с использованием оператора «:=». Например, для системы двух уравнений с двумя неизвестными, записанных в виде матриц, можно использовать следующий код:

A := [[2, 1], [1, 3]]
B := [5, 7]
X := linsolve(A, B)

Решение будет выведено как матрица \(X\), которая удовлетворяет уравнению \( A \cdot X = B \).

В случае вырождённых матриц Mathcad может предложить использование метода наименьших квадратов для получения приближённого решения, что особенно важно для систем, где матрица \(A\) не имеет инвертируемости. Для этого применяется функция \(\texttt{pinv}\), которая вычисляет псевдообратную матрицу через сингулярное разложение. Пример:

A := [[1, 2], [2, 4]]
B := [3, 6]
A_pinv := pinv(A)
X := A_pinv * B

Также Mathcad предоставляет возможность использовать LU-разложение для решения систем. Этот метод делит матрицу \(A\) на произведение нижней (L) и верхней (U) треугольных матриц, что позволяет повысить вычислительную эффективность при решении системы уравнений. Пример применения:

LU := ludecomp(A)
X := lusolve(LU, B)

Mathcad поддерживает решение как малых, так и крупных систем линейных уравнений, оптимизируя вычисления для больших матриц, что особенно важно при работе с многомерными задачами. В случае необходимости работы с большими объёмами данных стоит использовать настройку параметров для ускорения вычислений через многозадачность.

Применение матричных уравнений для анализа динамических систем

Для системы первого порядка, описываемой уравнением Ax = b, где A – матрица коэффициентов, x – вектор состояния, а b – вектор внешних воздействий, матричные методы обеспечивают компактное представление динамики. Важно, что такие системы могут быть преобразованы в уравнения высших порядков, что упрощает анализ их поведения в условиях различных параметров системы.

В применении к динамическим системам важное значение имеют собственные значения и собственные векторы матрицы системы. Эти параметры помогают определить устойчивость системы. Например, если все собственные значения матрицы A имеют отрицательные вещественные части, то система является устойчивой, что является необходимым условием для её стабильности.

Использование матричных уравнений в Mathcad позволяет проводить численный анализ сложных динамических систем. В частности, можно автоматически решать системы линейных дифференциальных уравнений с помощью встроенных функций, таких как odesolve, что значительно ускоряет процесс моделирования и анализа. Важно отметить, что Mathcad поддерживает работу с матричными уравнениями в символьной и числовой форме, что позволяет пользователю гибко выбирать подходящий метод в зависимости от специфики задачи.

Кроме того, для систем с временными задержками или нелинейностями, можно использовать расширенные подходы, такие как матричные уравнения с параметрической зависимостью или методы регуляризации, которые также реализуются в Mathcad. Эти методы позволяют учитывать изменения во внешней среде и корректировать поведение системы в реальном времени.

Таким образом, матричные уравнения являются неотъемлемой частью анализа и моделирования динамических систем, давая возможность проводить точный расчет их характеристик и принимать оптимальные решения для управления такими системами.

Интеграция матричных уравнений с другими математическими операциями в Mathcad

Mathcad предлагает мощные инструменты для работы с матричными уравнениями, позволяя их интеграцию с различными математическими операциями. Матричные уравнения могут эффективно сочетаться с операциями алгебры, дифференцирования, интегрирования, а также решением дифференциальных уравнений и оптимизацией.

Один из ключевых аспектов интеграции – это возможность использования матриц в качестве операндов для базовых математических операций, таких как сложение, вычитание, умножение, деление и транспонирование. Например, при решении систем линейных уравнений можно комбинировать матрицы с операциями умножения и обратного действия, что помогает моделировать и анализировать реальные системы.

Mathcad поддерживает использование матриц с операциями дифференцирования и интегрирования. Для этого можно использовать символические вычисления для вычисления производных или интегралов от элементов матриц. Это дает возможность моделировать динамические системы, где матрицы описывают состояние системы во времени, а производные показывают изменения этих состояний. Интеграция таких операций с решением матричных уравнений позволяет анализировать системы с учетом их временной эволюции.

Для более сложных математических моделей Mathcad также предоставляет инструменты для работы с матричными уравнениями в контексте численных методов. Например, можно интегрировать матричные уравнения с числовыми решателями дифференциальных уравнений, таких как метод Эйлера или Рунге-Кутты. Это полезно при моделировании систем с переменными коэффициентами, где требуется учесть динамическую изменчивость системы на каждом шаге.

Также Mathcad позволяет интегрировать матричные операции с операциями оптимизации. Матричные уравнения могут быть использованы в контексте задачи минимизации или максимизации функций, где матрицы играют роль параметров или переменных. Например, при решении задачи линейного программирования можно комбинировать матричные уравнения с операциями оптимизации для нахождения наилучших значений переменных.

Для эффективной работы с матричными уравнениями в Mathcad важно понимать возможности комбинирования различных операций и правильное использование инструментов для достижения нужных результатов. Совмещение матричных уравнений с другими математическими операциями позволяет значительно расширить спектр решаемых задач и повысить точность моделирования.

Решение нелинейных матричных уравнений с использованием численных методов

Основная трудность при решении нелинейных матричных уравнений заключается в том, что они могут иметь несколько решений или даже не иметь решения в принципе. Например, при попытке решить уравнение вида A(X) = B, где A(X) – это нелинейная функция от матрицы X, важно учитывать, что у этой функции могут быть особые точки или она может быть неограниченно растущей, что затрудняет её решение.

При использовании численных методов, таких как метод Ньютона или градиентный спуск, основным моментом является правильная постановка задачи и выбор начальных значений. Метод Ньютона часто используется для решения таких уравнений за счет использования производных и якобианов. Важно отметить, что для точности решения необходимо правильно оценивать градиенты и особенности матричных функций, особенно при работе с большими матрицами, где вычислительная сложность возрастает.

Одним из эффективных способов ускорения вычислений является использование метода минимизации невязки. В этом подходе цель сводится к минимизации функции невязки, которая определяется как разница между матричным выражением и правой частью уравнения. Для этого можно применить методы, такие как метод наименьших квадратов или градиентный спуск с адаптивной корректировкой шагов.

Важным моментом является выбор критериев сходимости алгоритма. Типично, для численных методов используется критерий достижения заданной точности на каждом шаге итерации. В некоторых случаях необходимо интегрировать дополнительные методы стабилизации, чтобы избежать проблем с расходимостью решений, особенно в условиях плохой обусловленности матрицы или при наличии малых собственных значений.

Кроме того, на решение нелинейных матричных уравнений влияет размерность матриц. В случае больших размерностей (например, свыше нескольких тысяч элементов) обычные итерационные методы могут привести к значительным затратам времени и памяти. Для работы с большими матрицами часто применяют методы разреженных матриц или алгоритмы, использующие многомерное разбиение, что позволяет значительно ускорить процесс вычислений.

В Mathcad для решения таких задач можно воспользоваться встроенными функциями и библиотеками, которые позволяют эффективно решать матричные уравнения методом Ньютона, градиентным спуском или методом наименьших квадратов. Важно понимать, что Mathcad предоставляет удобные средства для визуализации процессов сходимости, что позволяет быстро анализировать эффективность выбранного численного метода.

Оптимизация алгоритмов решения матричных уравнений в Mathcad

Mathcad предоставляет пользователям гибкие возможности для решения матричных уравнений, однако для повышения эффективности и точности работы с большими системами уравнений необходимо учитывать несколько аспектов оптимизации. Рассмотрим ключевые стратегии, которые помогут повысить производительность алгоритмов в Mathcad.

1. Использование специализированных функций

Mathcad включает в себя несколько встроенных функций для работы с матрицами, таких как linsolve(), inv() и det(). Однако для больших матриц стандартные методы могут быть медленными. Рекомендуется использовать более специализированные функции, такие как QR-разложение или LU-разложение, которые обеспечивают более быстрые решения при наличии разреженных матриц.

2. Снижение сложности алгоритмов

Если матричное уравнение имеет структуры, которые позволяют выделить подзадачи, следует использовать методы разбиения задачи на более простые этапы. Например, если известен блок-диагональный характер матрицы, можно решить уравнение по частям, что значительно снижает вычислительные затраты.

3. Использование числовых методов для приближенных решений

Для уравнений, где точное решение затруднительно или невозможно, полезно использовать числовые методы, такие как метод Гаусса, метод наименьших квадратов или метод Ньютона. Эти методы помогают найти приближенные решения с нужной точностью, что ускоряет процесс при больших объемах данных.

4. Уменьшение объема данных

Для работы с большими матрицами следует избегать работы с полными матрицами, если это возможно. Вместо этого можно использовать разреженные матрицы, которые в Mathcad поддерживаются через функции, такие как Sparse(). Разреженные матрицы позволяют существенно снизить потребление памяти и ускорить вычисления.

5. Параллельные вычисления

Mathcad поддерживает параллельные вычисления, что позволяет значительно ускорить решение сложных матричных уравнений. Для этого можно использовать возможность многозадачности на многоядерных процессорах. Операции с матрицами, например, умножение или обращение, могут быть параллелизованы, что снизит время решения задачи.

6. Профилирование производительности

Для оптимизации выполнения алгоритмов следует регулярно проводить профилирование производительности. Mathcad предоставляет инструменты для измерения времени выполнения различных блоков кода, что помогает выявить узкие места в вычислениях. Например, можно использовать встроенные функции для измерения времени и ресурсоемкости операций, что поможет улучшить скорость алгоритмов.

7. Использование векторных операций

Mathcad оптимизирует вычисления при использовании векторных операций, а не поэлементных циклов. Вместо того чтобы перебирать элементы матрицы в цикле, лучше использовать векторизацию, которая позволяет выполнять операции с большими массивами данных одновременно, что заметно ускоряет выполнение программы.

Внедрение этих методов и стратегий оптимизации позволяет существенно повысить эффективность работы с матричными уравнениями в Mathcad, особенно при решении сложных задач, требующих значительных вычислительных ресурсов.

Практические примеры применения матричных уравнений в инженерных расчетах

Для расчета прочности и устойчивости конструкций применяется метод конечных элементов (МКЭ), где система уравнений, описывающих поведение элементов конструкции, сводится к матричным формулам. Каждый элемент конструкции описывается собственными матрицами жесткости, а общая матрица жесткости системы получается путем сборки этих матриц для всей конструкции. Решение матричного уравнения позволяет получить распределение усилий и деформаций по всем элементам.

Другим примером является расчет электрических цепей с использованием метода узловых потенциалов. Здесь система уравнений для напряжений и токов сводится к матричным формулам, где коэффициенты матриц представляют собой элементы сопротивлений и индуктивностей элементов цепи. Решение этого уравнения позволяет вычислить токи в каждом из элементов цепи для заданных источников напряжения.

В теплотехнических расчетах, например, для моделирования тепловых процессов в системах с несколькими теплообменниками, используются матричные уравнения для описания теплопередачи между элементами. Каждое из уравнений описывает тепловой поток через конкретный теплообменник и связывает температуры различных частей системы. Комплексное решение этой системы с помощью матричных методов позволяет прогнозировать поведение системы при различных режимах работы.

В аэродинамике матричные уравнения применяются для моделирования потоков воздуха вокруг летательных аппаратов. Используя методы, такие как метод численного моделирования на сетке, можно сформировать систему уравнений для вычисления скорости и давления в различных точках поля потока. Решение системы дает информацию о распределении аэродинамических характеристик, которые критичны для проектирования и оптимизации летательных аппаратов.

В системах автоматического управления, например, для моделирования динамики роботов или автономных транспортных средств, матричные уравнения используются для описания взаимосвязей между входами и выходами системы. Матричное представление позволяет эффективно решать задачи стабилизации, оптимизации и предсказания поведения системы на основе текущих данных.

При решении задач оптимизации в инженерных расчетах, таких как минимизация расхода материалов или энергии, также часто используются матричные уравнения. Например, в задачах линейного программирования матрицы коэффициентов ограничений и целевой функции позволяют сформулировать и решить задачу с использованием методов линейной алгебры.

Вопрос-ответ:

Что такое матричные уравнения в Mathcad и как их решать?

Матричные уравнения в Mathcad представляют собой системы линейных уравнений, в которых неизвестными являются матрицы. Решение таких уравнений можно выполнить с помощью встроенных функций Mathcad, таких как «linsolve» для решения линейных систем или «inv» для нахождения обратной матрицы. Важно правильно задать размерность матриц и убедиться в их совместимости для вычислений. Mathcad предоставляет удобный интерфейс для работы с матрицами, автоматически учитывая порядок операций.

Как в Mathcad можно вычислить решение системы матричных уравнений с несколькими неизвестными?

Для вычисления решения системы матричных уравнений с несколькими неизвестными в Mathcad используется метод подстановки и методы линейной алгебры, такие как разложение или использование обратной матрицы. Система уравнений обычно имеет вид: A * X = B, где A и B — известные матрицы, а X — матрица, которую нужно найти. Используя команду «linsolve», можно решить такую систему, если она совместна, или найти псевдорешение, если система не имеет точного решения.

Какие особенности работы с матричными уравнениями в Mathcad отличаются от других программ для вычислений?

Mathcad отличается от других программ тем, что в нем можно работать с матрицами и уравнениями в их «естественном» виде, используя математические выражения, которые легко воспринимаются пользователем. В отличие от более сложных языков программирования или пакетов вроде MATLAB, Mathcad не требует глубоких знаний синтаксиса, а вывод результатов происходит в виде хорошо оформленных математических выражений, что делает работу с матричными уравнениями удобной и наглядной. Также, Mathcad позволяет настраивать визуальное представление данных, что важно при анализе больших массивов информации.

Для чего можно использовать матричные уравнения в Mathcad в реальной практике?

Матричные уравнения в Mathcad находят применение в различных областях, таких как механика, экономические модели, обработка изображений и другие инженерные задачи. Например, в физике можно моделировать системы с несколькими степенями свободы, а в экономике — решать задачи оптимизации с множеством переменных. Благодаря интеграции с другими расчетными функциями Mathcad, можно эффективно решать задачи оптимизации, прогнозирования или моделирования систем.

Какие трудности могут возникнуть при решении матричных уравнений в Mathcad?

Основные трудности при решении матричных уравнений в Mathcad могут возникнуть из-за некорректного задания размерности матриц или их несовместимости для решения. Также, если система уравнений вырождается или имеет более одного решения, это может создать дополнительные сложности. В таких случаях полезно использовать методы численного анализа, такие как метод наименьших квадратов, чтобы получить приближенное решение. Для решения таких проблем важно внимательно проверять входные данные и корректно интерпретировать результаты.

Что такое матричные уравнения в Mathcad и как они используются в решении инженерных задач?

Матричные уравнения в Mathcad — это математические выражения, содержащие матрицы, которые могут быть использованы для моделирования различных инженерных и научных процессов. В Mathcad эти уравнения позволяют быстро и наглядно работать с большими массивами данных. Например, они применяются для решения систем линейных уравнений, анализа устойчивости систем или оптимизации процессов. Mathcad предоставляет удобные инструменты для ввода, вычислений и визуализации результатов, что делает работу с такими уравнениями более доступной и понятной для инженеров и ученых.

Какие особенности работы с матричными уравнениями в Mathcad важно учитывать?

При работе с матричными уравнениями в Mathcad следует учитывать несколько важных особенностей. Во-первых, Mathcad поддерживает работу с матрицами различных размеров и типов, включая квадратные, прямоугольные, разреженные и плотные матрицы. Это дает возможность эффективно решать задачи с различными условиями. Во-вторых, важно правильно настроить операции умножения и сложения матриц, так как Mathcad автоматически проверяет совместимость размеров матриц, что минимизирует вероятность ошибок. Также стоит отметить наличие встроенных функций для вычисления детерминантов, обратных матриц, собственных значений и других важных характеристик матриц. Наконец, Mathcad позволяет визуализировать результаты в виде графиков или таблиц, что упрощает анализ и интерпретацию данных.