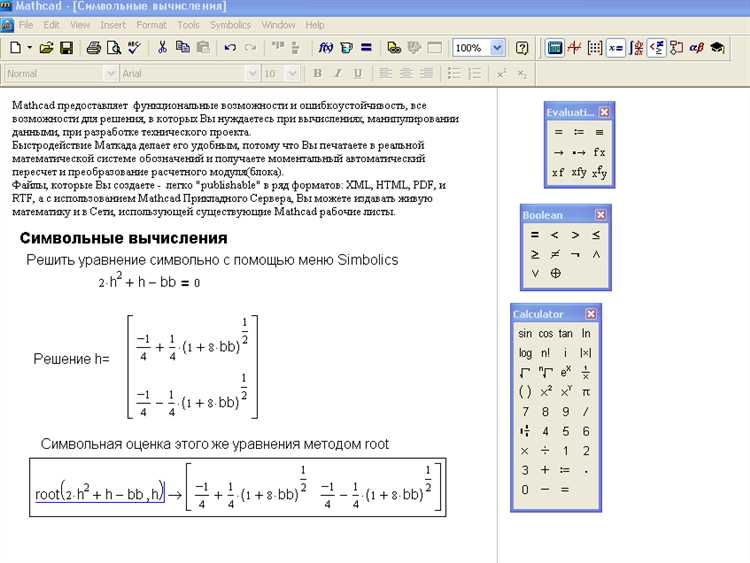
Mathcad применяется для документирования и автоматизации инженерных расчётов, объединяя численные вычисления с текстовыми пояснениями и визуализацией. В отличие от электронных таблиц, в Mathcad используется привычный математический синтаксис: формулы отображаются в стандартной нотации, что облегчает верификацию и передачу данных между специалистами.
Программа поддерживает расчёты с переменными, массивами, единицами измерения и встроенными функциями. При задании физических величин можно задать размерность, и система автоматически приведёт результат к требуемой единице. Это особенно удобно при расчётах в теплоэнергетике, гидравлике и механике, где важно контролировать размерности выражений.
Mathcad Prime позволяет использовать условные операторы, циклы, символьные вычисления, интегралы, дифференциалы и уравнения. Пользователь может составить модель, в которой параметры меняются автоматически при изменении входных данных, что удобно для проектных и оптимизационных задач.
Для построения графиков Mathcad предоставляет двух- и трёхмерные визуализации. Это удобно при анализе функций, результатах численного моделирования и контроле пограничных условий. Кроме того, доступна вставка чертежей, комментариев и пояснительных записок, что делает Mathcad средой не только расчёта, но и отчётности.
Рекомендуется использовать Mathcad при разработке технической документации, оформлении расчётных записок, проверке проектных решений и обучении. Программа интегрируется с Excel и CAD-системами, может экспортировать данные в форматы PDF, XPS и HTML, а также поддерживает защиту содержимого через блокировку или шифрование областей.
Построение и решение систем линейных уравнений в Mathcad
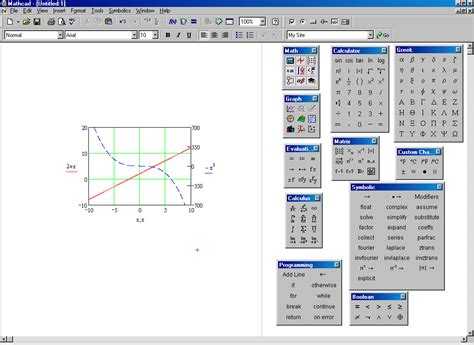
Для задания системы линейных уравнений в Mathcad удобно использовать матричную форму. Коэффициенты уравнений записываются в виде матрицы A, свободные члены – вектор b. Решение системы Ax = b находится через встроенный оператор «обратная матрица» или с помощью функции lsolve(A, b).
Матрица вводится через клавишу [Ctrl]+M или пункт меню «Вставка» → «Матрица». Размерность указывается вручную. После ввода матрицы A и вектора b создаётся переменная x := lsolve(A, b). Mathcad автоматически рассчитает вектор решений x при условии, что матрица A квадратная и невырожденная.
Если матрица вырождена или система несовместна, Mathcad выдаёт сообщение об ошибке. Для проверки обратимости можно использовать оператор det(A). Если определитель равен нулю, система не имеет единственного решения.
Для символьного решения используется знак Ctrl + . или контекстное меню «Символьное вычисление». Уравнения задаются поэлементно, каждое – на отдельной строке. Например:
2*x + y = 5
x - 3*y = -4
Затем вызывается символьная команда solve({уравнения}, {переменные}). Mathcad вернёт точное аналитическое решение, если оно существует.
Для систем с параметрами удобно использовать символьные выражения – это позволяет отслеживать влияние коэффициентов на результат без численного подстановки. Это особенно полезно в инженерных задачах при работе с переменными нагрузками или материалами.
Если система переопределена (уравнений больше, чем переменных), применяется функция minerr(A, b), которая вычисляет вектор x, минимизирующий среднеквадратичную погрешность. Это актуально при обработке экспериментальных данных и задачах аппроксимации.
Использование встроенных функций для расчёта параметров схем
Mathcad содержит набор встроенных функций, позволяющих выполнять расчёты электрических, тепловых и механических схем без необходимости вручную задавать формулы. Это упрощает моделирование и анализ при проектировании.
- Ом закон и цепи постоянного тока: функции
solveиgivenпозволяют находить токи и напряжения в узлах и ветвях. Для символьных расчётов удобно использоватьsymbolic. - RC- и RL-цепи: функция
exp()применяется для моделирования переходных процессов. Решение дифференциальных уравнений можно автоматизировать черезdesolve. - Комплексные схемы: встроенные функции
Re(),Im(),abs(),arg()позволяют анализировать амплитуду и фазу в цепях переменного тока. - Импеданс: для расчёта полного сопротивления используется комбинация
j,omegaи арифметических операций. Например, для индуктивности:Z_L := j * omega * L. - Резонанс: частота резонанса LC-контура вычисляется через
f := 1 / (2 * π * sqrt(L * C)). Все параметры можно задать как переменные, что позволяет быстро изменять входные данные. - Матричный анализ: функции
augment(),rowreduce(),invert()полезны при работе с методами узловых потенциалов и контурных токов.
При расчётах важно задавать единицы измерения, чтобы избежать ошибок. Mathcad автоматически проверяет размерность выражений и сигнализирует о несоответствиях. Использование unit-функций позволяет задать, например, V := 5 * V, R := 1.2 * kΩ, что делает расчёты наглядными и корректными.
Для повторяющихся операций целесообразно использовать пользовательские функции. Например, для расчёта делителя напряжения:
VoltageDivider(Vin, R1, R2) := Vin * R2 / (R1 + R2)Встроенные функции позволяют сосредоточиться на логике схемы, минимизируя рутинные вычисления.
Численное интегрирование инженерных задач в Mathcad
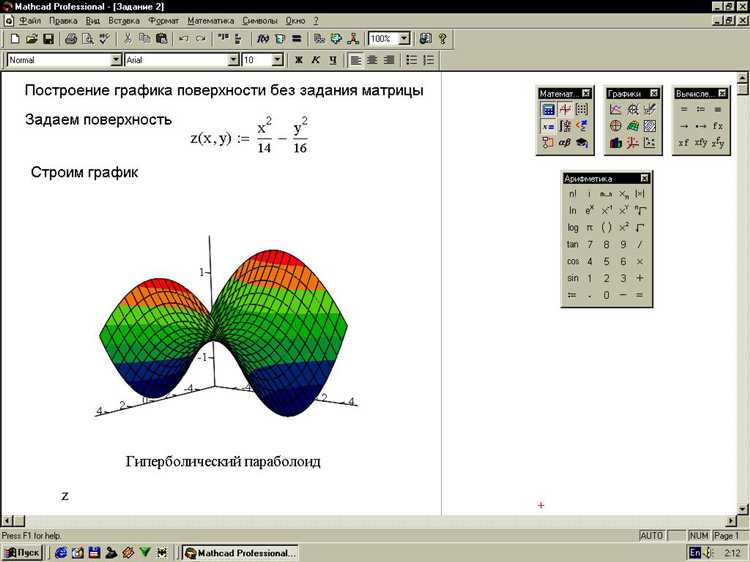
Mathcad предоставляет встроенные функции для численного интегрирования, которые позволяют решать задачи, где аналитическое решение невозможно или затруднено. Ключевая функция – int(), выполняющая интегрирование по заданным пределам.
Для одномерного интегрирования используется синтаксис: int(f(x), x, a, b), где f(x) – подынтегральная функция, a и b – пределы интегрирования. Mathcad автоматически применяет адаптивные методы, включая метод Симпсона и квадратурные формулы Гаусса, в зависимости от сложности функции.
При необходимости интегрирования табличных данных Mathcad применяет интерполяцию. Используется функция interp(x, X, Y), где X и Y – векторы значений, а x – аргумент. Полученную интерполированную функцию можно подставить в int().
Для двойных и тройных интегралов применяются вложенные вызовы int() с явным указанием переменных. Например: int(int(f(x,y), y, y1, y2), x, x1, x2).
Если функция содержит разрывы или участки с высокой кривизной, рекомендуется предварительно визуализировать график функции и по возможности разбивать интеграл на несколько участков. Это повышает точность численного результата.
Mathcad позволяет задавать переменные верхнего и нижнего предела, что удобно при параметрических исследованиях. Также можно использовать операторы range для пошагового расчёта значений интегралов при изменении параметров.
В инженерной практике часто интегрируются нагрузки, тепловые потоки, расходные характеристики. Mathcad позволяет объединять численное интегрирование с символьными выражениями, уравнениями состояния и единицами измерения, обеспечивая согласованность всех расчётов без необходимости ручного контроля размерностей.
Автоматизация расчётов с помощью пользовательских функций
В Mathcad пользовательские функции позволяют структурировать расчёты, уменьшить количество повторяющихся операций и снизить вероятность ошибок. Они особенно полезны при работе с многократно используемыми выражениями, типовыми алгоритмами и инженерными стандартами.
- Функции создаются через оператор :=, за которым следует имя функции, список аргументов в скобках и выражение.
- Имена функций должны быть уникальными и не конфликтовать с встроенными.
- Функции могут принимать числовые и векторные аргументы, а также возвращать массивы.
Пример: функция для расчёта допусков по системе отверстия:
Допуск(ES, EI) := ES - EI
Для типовых инженерных задач рекомендуется выносить расчёты в отдельные функции:
- Повышается читаемость документа за счёт отделения логики расчётов от данных.
- Можно повторно использовать функции в других проектах, копируя блок или сохраняя в библиотеке.
- При изменении формулы правка происходит в одном месте.
Для ускорения работы с большим количеством однотипных расчётов (например, подбор сечений, расчёт прочности, потерь давления) удобно создавать обобщённые функции с параметрами, передающими характеристики материала, геометрии и нагрузки.
Рекомендуется:
- Избегать жёсткой привязки функций к единицам измерения, использовать автоопределение единиц Mathcad.
- Добавлять короткие комментарии рядом с определениями функций для пояснения логики.
- Проверять граничные случаи при тестировании пользовательских функций.
Сложные пользовательские функции можно объединять в отдельные листы и подключать в основной расчёт через Insert → Reference, что особенно полезно при работе в команде или создании корпоративных шаблонов.
Графическое представление результатов расчётов

Mathcad поддерживает встроенное построение графиков по численным массивам, функциям и параметрическим зависимостям. Для получения графика достаточно задать диапазон переменных и формулу, после чего выбрать тип графика: 2D или 3D.
Для 2D-графиков рекомендуется использовать оператор «plot» с явным указанием диапазона по оси X. Например, при построении функции напряжения в балке следует задать длину пролёта как диапазон X и использовать соответствующую формулу для расчёта изгибающего момента или напряжений.
3D-графики позволяют анализировать поведение многопараметрических функций. Например, распределение температуры по пластине моделируется через матрицу значений в зависимости от координат X и Y. Для наглядности можно применять цветовую заливку по шкале значений.
Графики автоматически обновляются при изменении входных данных, что удобно для анализа чувствительности параметров. При этом важно проверять масштаб осей и границы построения: Mathcad не обрезает значения автоматически, что может привести к искажению восприятия.
Для точечной визуализации результатов эксперимента или численного моделирования рекомендуется использовать маркеры данных. Например, при сравнении расчётной и экспериментальной кривой нагрева тела удобно нанести обе зависимости на один график с различными стилями линий и точек.
Подписи осей, единицы измерения и сетка задаются вручную в панели настроек. Это критично при оформлении графиков для отчётов и презентаций. Подписи должны отражать физический смысл переменных: не «X» и «Y», а, например, «Температура, °C» и «Время, с».
При работе с массивами, содержащими разрывы или нули, следует избегать деления на ноль и использовать функции проверки допустимости значений. Mathcad не игнорирует такие точки и может некорректно отобразить график.
Импорт и обработка экспериментальных данных в Mathcad
Для импорта экспериментальных данных в Mathcad используется функция READPRN, принимающая путь к текстовому файлу с разделителями табуляции или пробелами. Формат данных должен соответствовать матричной структуре: строки – измерения, столбцы – параметры.
Если требуется работа с CSV-файлами, применяется READCSV. При этом поддерживаются как числовые значения, так и текстовые заголовки. После импорта рекомендуется проверка структуры с помощью rows() и cols(), чтобы убедиться в корректной загрузке.
Для фильтрации и предварительной обработки можно использовать логические маски. Например, чтобы исключить выбросы, создаётся булева матрица по условию, а затем применяется индексирование. Для сглаживания данных часто используют скользящее среднее с циклической реализацией или встроенными функциями.
Математическая аппроксимация осуществляется через функцию linfit (линейная) или genfit (пользовательская модель). Результаты аппроксимации визуализируются с помощью plot, где исходные и смоделированные данные отображаются на одном графике для оценки точности.
Для интерполяции применяется interp или interp2 в случае двумерных данных. Перед интерполяцией массивы должны быть отсортированы. Нарушение этого условия приводит к ошибкам выполнения.
Все операции сохраняются как часть документа, позволяя отслеживать изменения и повторно использовать расчёты без необходимости повторного импорта.
Подготовка расчётных пояснений с оформлением в формате отчёта
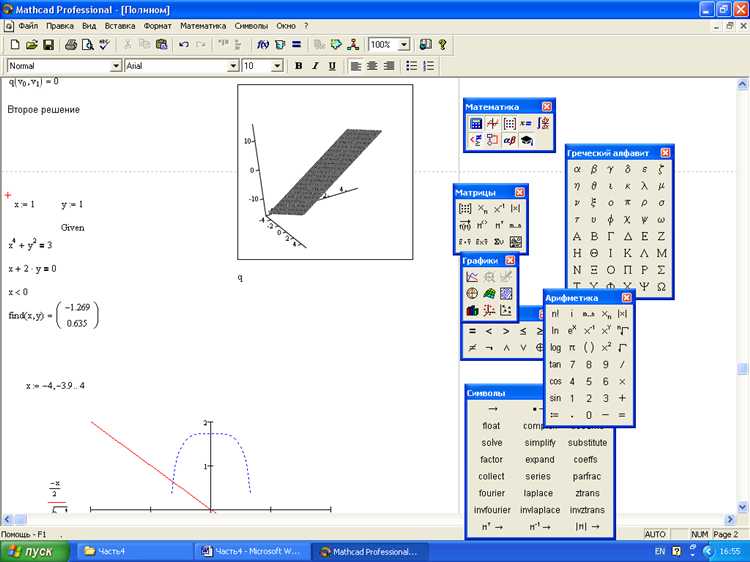
Рекомендуется использовать встроенные текстовые блоки для пояснений, пояснять каждый этап вычислений и комментировать результаты. Это обеспечивает читаемость и повторяемость расчётов. Размерность выражений контролируется автоматически, что исключает ошибки при преобразованиях единиц.
Графики следует размещать рядом с соответствующими расчётами. Под каждым графическим элементом указывается подпись, описывающая отображаемые зависимости. Если расчёты многоступенчатые, между блоками вычислений желательно вставлять короткие текстовые пояснения, уточняющие цель каждого этапа.
В завершение отчёта целесообразно добавить сводную таблицу с результатами:
| Параметр | Обозначение | Значение | Ед. изм. |
|---|---|---|---|
| Момент инерции балки | I | 3.2×10⁶ | мм⁴ |
| Максимальное напряжение | σmax | 145 | МПа |
| Коэффициент запаса | n | 1.75 | — |
При экспорте в PDF сохраняется весь формат Mathcad-документа, включая шрифты, расположение блоков, изображения и таблицы. Это позволяет использовать такой файл как официальную часть проектной документации без дополнительного редактирования.
Работа с размерностями и единицами измерения в Mathcad
Mathcad поддерживает автоматическое отслеживание размерностей, что позволяет избежать ошибок при расчетах. Все переменные могут иметь физическую размерность, и Mathcad проверяет согласованность единиц во всех выражениях.
Для задания размерности используется оператор умножения на единицу. Например, чтобы задать длину в метрах, пишут: L := 5 * m. Mathcad распознаёт международную систему единиц (СИ), а также позволяет использовать производные и внесистемные единицы, включая дюймы, фунты, атмосферы и другие.
Результаты вычислений автоматически приводятся к базовым единицам СИ, но пользователь может указать, в каких единицах должен быть представлен результат. Для этого применяют оператор →. Пример: L := 3 * ft, затем L → m выведет длину в метрах.
Mathcad позволяет создавать пользовательские единицы. Например: 1 bar := 10^5 * Pa. После этого P := 2 * bar и P → Pa будут корректно интерпретированы системой.
Для отображения размерности результата вместе с числовым значением используется оператор → без указания единицы. Пример: v := 20 * km/h, затем v → выведет значение в м/с с размерностью.
Если необходимо избавиться от размерностей и получить безразмерный результат, используется функция unitless. Пример: unitless(L / m) вернёт числовое значение длины в метрах без размерности.
Mathcad автоматически сигнализирует о несогласованности размерностей. Например, попытка сложить векторы, выраженные в разных единицах, вызовет ошибку, если они не приведены к совместимым размерностям.
Для контроля за единицами удобно использовать встроенные единицы в палитре или вводить их вручную через клавиатуру. Mathcad корректно обрабатывает сложные выражения с несколькими размерностями, включая производные, интегралы и системы уравнений.
Вопрос-ответ:
Для каких типов инженерных задач Mathcad подходит лучше всего?
Mathcad хорошо справляется с расчетами, связанными с механикой, электротехникой, термодинамикой и строительством. Он удобен для анализа уравнений, проведения численных расчетов и построения графиков, что позволяет быстро проверить и визуализировать результаты. Особенно полезен при необходимости формализовать сложные математические зависимости и связать их с текстовыми пояснениями.
Какие преимущества Mathcad даёт по сравнению с традиционными табличными процессорами?
В отличие от табличных процессоров, Mathcad позволяет записывать математические выражения в привычном виде, а не в виде формул в ячейках. Это упрощает понимание и проверку расчетов. Кроме того, Mathcad автоматически следит за размерностями, помогает избегать ошибок в единицах измерения и умеет строить графики по формулам без дополнительного программирования.
Насколько сложен процесс обучения работе с Mathcad для инженера без опыта программирования?
Интерфейс Mathcad построен так, чтобы максимально приблизить работу с расчетами к привычному письму на бумаге. Многие инженеры без опыта программирования быстро осваивают базовые функции — запись уравнений, вычисления, создание графиков. Для более сложных операций есть встроенные библиотеки и шаблоны. Время на освоение зависит от глубины использования, но основные задачи решаются без серьёзных трудностей.
Как Mathcad помогает контролировать ошибки в расчетах?
Mathcad автоматически проверяет размерности, что снижает риск ошибок из-за неправильного использования единиц измерения. При внесении изменений в исходные данные программа пересчитывает все связанные выражения, предотвращая забытые обновления. Кроме того, наличие текстовых комментариев и структурированного документа помогает лучше проследить логику расчетов и обнаружить возможные неточности.
Можно ли использовать Mathcad совместно с другими инженерными программами?
Да, Mathcad поддерживает импорт и экспорт данных в различных форматах, что позволяет интегрировать его с CAD-системами, системами автоматизированного проектирования и аналитическими программами. Также возможна работа с внешними скриптами и подключение пользовательских библиотек, что расширяет его возможности и упрощает обмен данными между разными инструментами в рамках инженерного процесса.