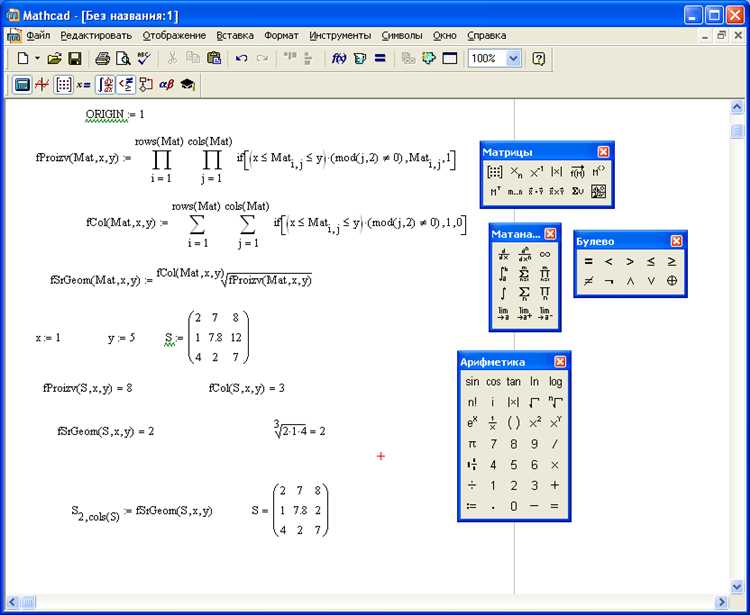
Единичная матрица – это квадратная матрица, у которой все элементы главной диагонали равны единице, а остальные – нулю. В Mathcad такую матрицу можно создать с помощью встроенной функции identity(n), где n – размерность матрицы. Функция возвращает матрицу размером n×n с единицами на главной диагонали.
Для практического применения важно учитывать, что Mathcad нумерует элементы массивов и матриц с нуля по умолчанию. Это может повлиять на индексирование, если вы вручную создаёте или проверяете элементы матрицы. При необходимости начальный индекс можно изменить через параметры документа.
При работе с единичной матрицей в Mathcad удобно использовать её как базу для построения других матриц, например, в численных методах решения систем линейных уравнений или при разработке алгоритмов линейной алгебры. Также возможно масштабирование единичной матрицы на скаляр, что полезно при работе с матрицами перехода и преобразованиями координат.
Функция identity не требует ручного ввода элементов, в отличие от создания матрицы с помощью команды matrix(n, m), что делает её предпочтительным инструментом при необходимости быстрого получения матрицы с заданными свойствами. Это особенно актуально при автоматизации вычислений и формализации математических моделей.
Как задать размерность единичной матрицы в Mathcad
Чтобы задать размерность, введите имя переменной, например A := identity(5). Это создаст квадратную матрицу 5×5, где все элементы главной диагонали равны 1, а остальные – 0. Mathcad автоматически распознает тип данных и отобразит результат в виде матрицы.
Размерность задается только одним аргументом, так как единичная матрица по определению всегда квадратная. Если необходимо использовать её в контексте матричных операций других размеров, примените функции транспонирования или обрезки, но начальная генерация всегда выполняется через identity(n).
Для изменения размерности достаточно изменить аргумент: identity(3) создаст матрицу 3×3, identity(10) – 10×10. Используйте переменные для динамического управления размером: n := 4, затем A := identity(n).
Использование встроенной функции identity
В Mathcad для создания единичной матрицы применяется функция identity(n), где n – целое положительное число, определяющее размер квадратной матрицы. Результатом будет матрица размером n×n с единицами на главной диагонали и нулями во всех остальных ячейках.
Функция identity вызывается без необходимости явного ввода нулей или единиц. Например, выражение identity(4) автоматически формирует следующую матрицу:
| 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 1 |
Если указать аргумент n = 1, возвращается скалярное значение 1, а не матрица. Для создания единичной матрицы другого размера необходимо использовать строго целое значение, превышающее 1. При попытке передать нецелое или отрицательное число возникает ошибка вычислений.
Функция identity не принимает второй аргумент. Для создания не квадратной матрицы с диагональю из единиц требуется использовать альтернативные методы, например, ручную инициализацию с помощью matrix и if-выражений.
Создание единичной матрицы вручную через индексацию
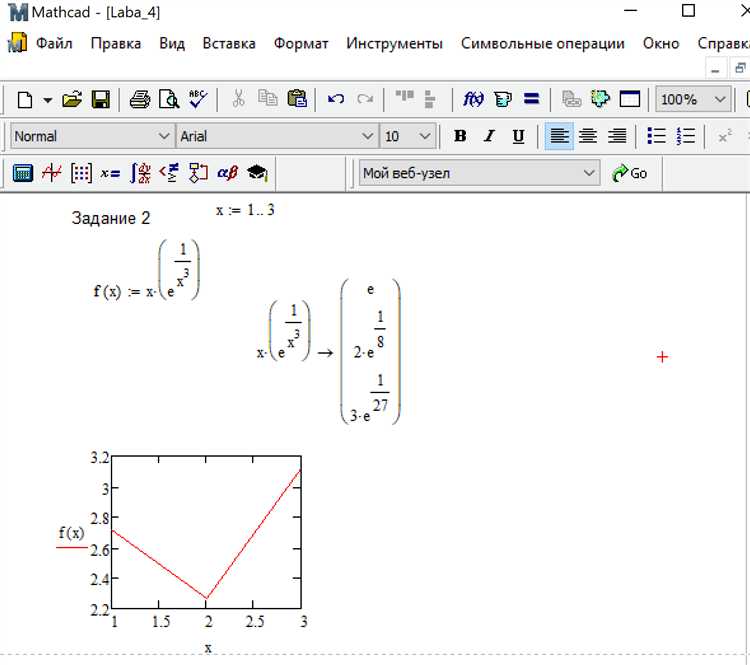
В Mathcad возможно создать единичную матрицу вручную, используя индексацию элементов. Такой подход необходим при отсутствии встроенных функций или при необходимости полного контроля над структурой матрицы.
- Задайте размерность матрицы: например,
n := 4для создания матрицы 4×4. - Создайте пустую матрицу нулей с нужными размерами:
A := matrix(n, n). - Произведите цикл по индексам от 0 до n–1:
- На каждой итерации присваивайте значение 1 только диагональному элементу:
A[i, i := 1 - Все остальные элементы остаются равными нулю.
Пример кода с использованием цикла for:
n := 4 A := matrix(n, n) for i := 0 .. n-1 A[i, i := 1
После выполнения цикла переменная A будет содержать единичную матрицу 4×4. Для других размерностей достаточно изменить значение n.
- Индексация в Mathcad начинается с нуля. Убедитесь, что параметр
ORIGINустановлен в 0. - Функция
matrix(m, n)создаёт матрицу m×n с нулями по умолчанию. - Редактировать отдельные элементы можно напрямую, указывая нужные индексы.
Проверка свойств единичной матрицы при умножении
В Mathcad для подтверждения свойств единичной матрицы используйте оператор умножения между матрицами. Создайте квадратную матрицу A размером 3×3, например:
A := [[2, -1, 0][0, 3, 4][1, 0, 5]]
Создайте единичную матрицу того же размера командой identity(3). Обозначьте её, например, как I:
I := identity(3)
Выполните умножение A на I:
A * I =
Mathcad отобразит результат, который должен быть идентичен исходной матрице A. Это подтверждает правостороннее свойство: A * I = A.
Затем проверьте левостороннее свойство:
I * A =
Результат снова должен быть равен A. Оба случая подтверждают, что единичная матрица действует как нейтральный элемент при умножении.
Для наглядного контроля можно использовать оператор сравнения = в Mathcad. Пример:
(A * I) = A
Если результат равен true, проверка выполнена корректно. Используйте это же правило для любых квадратных матриц других размеров. Несовпадение укажет на ошибку в размерах или неверную операцию.
Различие между единичной и диагональной матрицей в Mathcad
В Mathcad единичная и диагональная матрицы создаются с помощью разных подходов и служат разным целям. Их главное различие заключается в значениях на диагонали и в структуре вне диагонали.
- Единичная матрица создается функцией
identity(n). Она формирует квадратную матрицу размеромn×n, где на главной диагонали расположены только единицы, а все остальные элементы равны нулю. - Диагональная матрица задается функцией
diag(v), гдеv– вектор. Элементы этого вектора размещаются на главной диагонали результирующей матрицы, остальные значения – нули. Размер матрицы зависит от длины вектора.
Основные различия:
- Значения на диагонали: у единичной матрицы – только 1; у диагональной – произвольные значения из вектора.
- Гибкость:
diag()позволяет задать любые значения на диагонали,identity()– строго фиксированные. - Форма:
identity(n)всегда возвращает квадратную матрицу;diag(v)может вернуть прямоугольную, если использовать вектор как столбец или строку.
Рекомендации:
- Используйте
identity(n)при необходимости построения матрицы для умножения без изменения исходного вектора. - Применяйте
diag(v)при необходимости весового умножения или при работе с собственными значениями.
Создание единичной матрицы в блоке программирования
В Mathcad единичная матрица формируется с помощью функции identity(), которую удобно использовать внутри блока программирования для динамического создания матриц заданного размера.
В блоке программирования необходимо объявить переменную размера, например n, и вызвать функцию identity(n). Это создаст квадратную матрицу размером n × n с единицами на диагонали и нулями вне её.
Важно учитывать, что размер n должен быть целым и положительным числом, иначе Mathcad вернёт ошибку или некорректный результат.
Для создания матрицы в блоке программирования можно использовать следующий синтаксис:
ИдентичнаяМатрица := identity(n)
Если требуется использовать матрицу в дальнейших вычислениях или циклах внутри блока, стоит предварительно проверить валидность размера и обработать исключения.
При необходимости генерации единичной матрицы нестандартного размера (например, прямоугольной), стандартная функция identity() не применима, и придётся создавать матрицу вручную с помощью циклов и условных операторов.
Работа с единичной матрицей в символических вычислениях

В Mathcad единичная матрица часто применяется в символических вычислениях для упрощения выражений и доказательств тождеств. При объявлении символической единичной матрицы важно задать размерность явно, чтобы избежать неоднозначностей при операциях с матрицами разного порядка.
Создание единичной матрицы выполняется с помощью функции identity(n), где n – размерность. В символическом контексте n может быть параметром или выражением, что позволяет работать с матрицами переменного размера.
Для символического умножения единичная матрица играет роль нейтрального элемента. Mathcad сохраняет символическую форму произведения, что позволяет аналитически проверять равенства и упрощать выражения, избегая численных приближений.
При обратном преобразовании символическая единичная матрица используется для проверки корректности вычисления обратной матрицы. Операция A × identity(n) = A служит базовой проверкой, и Mathcad подтверждает это в символической форме без раскрытия конкретных значений.
Для дифференцирования выражений с единичной матрицей важно учитывать, что она не зависит от переменных и производная равна нулю. Это упрощает вычисления при работе с символическими матрицами, содержащими параметрические элементы.
Mathcad позволяет комбинировать единичную матрицу с другими символическими объектами, сохраняя алгебраические свойства. Рекомендуется избегать неявных преобразований, чтобы сохранить точность символических результатов.
Вопрос-ответ:
Как в Mathcad создать единичную матрицу заданного размера?
В Mathcad для создания единичной матрицы используется встроенная функция, которая принимает на вход размер матрицы. Например, если требуется матрица размера 3 на 3, нужно ввести команду с указанием числа 3, и программа сформирует матрицу с единицами на диагонали и нулями в остальных ячейках.
Можно ли в Mathcad сделать единичную матрицу не только квадратной, но и прямоугольной?
Стандартная единичная матрица по определению квадратная, так как единицы расположены только на главной диагонали. В Mathcad функция создания единичной матрицы рассчитана именно на квадратные размеры. Если нужно получить прямоугольный массив с единицами на диагонали, потребуется создавать его вручную или с помощью пользовательских формул.
Что делать, если после создания единичной матрицы в Mathcad нужно изменить ее размер?
Изменение размера уже созданной матрицы напрямую в Mathcad невозможно. Лучше создать новую единичную матрицу нужного размера, используя соответствующую функцию с новым параметром. Если же нужна матрица с частично изменённым размером, можно комбинировать несколько матриц или использовать операции с индексами.
Какие ошибки могут возникнуть при попытке создать единичную матрицу в Mathcad?
Чаще всего ошибки связаны с неправильным вводом параметров, например, указанием нецелого или отрицательного числа размера. Также возможны проблемы, если забыть использовать функцию создания единичной матрицы, пытаясь задать её вручную с ошибками в индексах или значениях элементов.
Можно ли использовать единичную матрицу, созданную в Mathcad, для решения систем уравнений?
Да, единичная матрица часто используется в Mathcad как элемент в алгебраических вычислениях, в частности при решении систем линейных уравнений. Она играет роль нейтрального элемента при умножении матриц и помогает проверять правильность вычислений или задавать начальные условия для итерационных методов.