MATLAB предоставляет мощные инструменты для работы с матрицами, которые являются основой многих вычислений в области научных исследований и инженерии. Создание и манипуляции с матрицами в этой среде включают несколько базовых операций, которые позволяют эффективно управлять данными. Для начала необходимо понимать, как правильно объявить матрицу, как получить доступ к её элементам и какие функции для работы с матрицами наиболее полезны.
Создание матрицы в MATLAB начинается с объявления переменной, которая будет содержать матрицу. Для создания матрицы можно использовать квадратные скобки. Например, чтобы создать матрицу размером 2 на 3, достаточно написать следующее:
A = [1 2 3; 4 5 6];Каждое число разделяется пробелами или запятыми внутри строки, а строки разделяются точкой с запятой. Это создаст матрицу:
[1 2 3
4 5 6]Доступ к элементам матрицы осуществляется с помощью индексов. Индексы в MATLAB начинаются с единицы. Чтобы получить элемент на позиции (1,2) матрицы A, используйте следующий код:
element = A(1,2);Также можно извлекать целые строки или столбцы. Например, чтобы извлечь первый столбец:
column = A(:,1);Основные операции с матрицами включают сложение, вычитание, умножение и транспонирование. Все эти операции могут быть выполнены с использованием стандартных операторов. Для транспонирования матрицы используется апостроф:
B = A';Чтобы умножить матрицу на скаляр, достаточно умножить её на число:
C = 2 * A;Для матричного умножения между двумя матрицами A и B необходимо использовать оператор *, при этом количество столбцов первой матрицы должно совпадать с количеством строк второй:
result = A * B;Функции для работы с матрицами включают inv() для нахождения обратной матрицы, det() для вычисления детерминанта и eig() для поиска собственных значений и векторов. Например:
inverse = inv(A);
determinant = det(A);
[eigenvalues, eigenvectors] = eig(A);В MATLAB есть множество функций для работы с матрицами, и овладение ими позволяет значительно повысить эффективность вычислений и анализа данных. Обучение основам работы с матрицами в этой среде поможет вам освоить более сложные концепции и методы обработки данных.
Как объявить матрицу вручную в MATLAB

Для объявления матрицы в MATLAB можно использовать квадратные скобки. Каждый элемент матрицы разделяется пробелами или запятыми в строках, а строки – точкой с запятой. Например, для создания матрицы 2×3 можно использовать следующий синтаксис:
A = [1 2 3; 4 5 6]
Это создаст матрицу с двумя строками и тремя столбцами:
A = 1 2 3 4 5 6
Если нужно создать матрицу с различными размерами, например, 3×3, можно написать:
B = [1 2 3; 4 5 6; 7 8 9]
Матрицы могут быть также и строковыми, например:
C = ['a' 'b'; 'c' 'd']
Можно использовать переменные для создания матриц. Например, если у вас есть переменная, содержащая вектор, вы можете создать матрицу:
x = [1 2]; y = [3 4]; M = [x; y]
Если элементы матрицы могут быть вычислены через выражения, MATLAB позволяет комбинировать числа и операции прямо в квадратных скобках. Например, для создания матрицы с числами, полученными из вычислений, можно использовать следующий код:
D = [1+2 3*4; 5/2 6-1]
Этот способ дает возможность гибко строить матрицы без необходимости их предварительного расчета в отдельной строке кода.
Использование встроенных функций для создания матриц
MATLAB предлагает множество встроенных функций для создания и инициализации матриц, что значительно упрощает работу с ними.
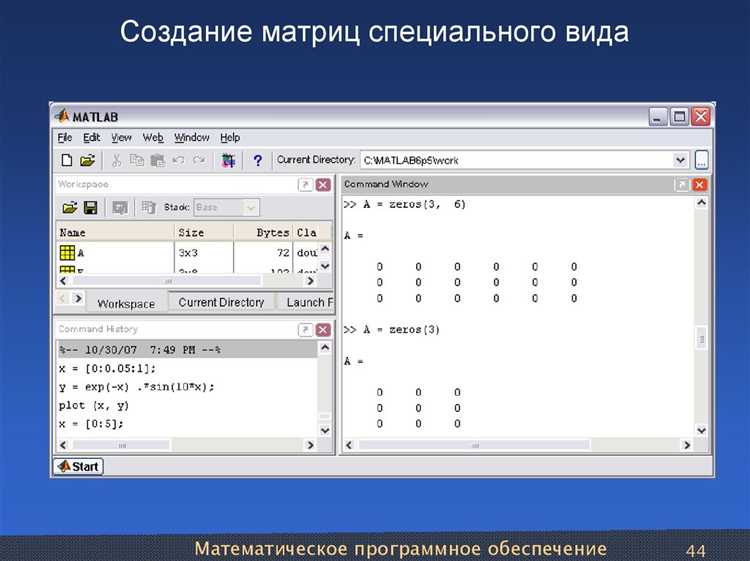
- zeros(m, n) – создаёт матрицу размера m на n, заполненную нулями. Это полезно, когда необходимо подготовить структуру данных, но значения ещё не определены.
- ones(m, n) – генерирует матрицу размера m на n, заполненную единицами. Она используется в задачах, где требуется стартовое значение всех элементов, равное 1.
- eye(n) – создаёт квадратную матрицу размером n на n с единицами на главной диагонали и нулями в остальных местах. Это идеальный инструмент для работы с единичными матрицами в линейной алгебре.
- diag(v) – создаёт диагональную матрицу из вектора v. Элементы вектора становятся элементами диагонали матрицы, а все остальные элементы равны нулю.
- rand(m, n) – создаёт матрицу размера m на n, заполненную случайными числами от 0 до 1. Подходит для моделирования случайных процессов и инициализации случайных весов в нейронных сетях.
- randn(m, n) – генерирует матрицу размера m на n с элементами, распределёнными по нормальному закону с нулевым математическим ожиданием и единичной дисперсией.
- linspace(a, b, n) – создаёт строку из n равномерно распределённых значений между a и b. Эта функция используется для построения диапазонов значений при решении уравнений или интерполяции.
- meshgrid(x, y) – создаёт двумерные массивы X и Y для использования в вычислениях, например, при построении поверхностей или графиков.
Каждая из этих функций имеет свои особенности, которые определяют её использование в различных задачах. Применение встроенных функций для создания матриц позволяет избежать написания лишнего кода и делает работу с матрицами в MATLAB более удобной и эффективной.
Как изменять размеры матрицы и добавлять новые элементы

В MATLAB работа с матрицами подразумевает изменение их размеров и добавление новых элементов. Для этого существует несколько методов, которые позволяют гибко работать с данными.
1. Изменение размера матрицы
Для изменения размера матрицы можно использовать оператор присваивания с новым размером. Это позволяет либо расширить, либо уменьшить матрицу.
- Чтобы увеличить матрицу, достаточно присвоить значения элементам вне текущих границ. Например:
A = [1 2 3; 4 5 6]; % Изначальная матрица 2x3 A(3,4) = 7; % Добавляем элемент в 3-й ряд и 4-й столбец, матрица станет 3x4
A = A(1:2, 1:3); % Оставляем только первые два ряда и три столбца
2. Добавление строк и столбцов
Новые строки или столбцы можно добавить через операторы конкатенации:
- Для добавления строки используйте:
A = [A; 7 8 9]; % Добавляем строку к матрице A
A = [A, 10; 11; 12]; % Добавляем столбец к матрице A
3. Применение функции resize
В MATLAB также есть встроенная функция resize для изменения размера матрицы, однако она работает только для определенных типов данных, таких как изображения. В большинстве случаев для изменения размера матрицы используются операции индексации или конкатенации.
4. Инициализация новых элементов
Если необходимо добавить элементы в пустую матрицу или произвести инициализацию с нуля, используется функция zeros, ones или nan для создания матрицы с заранее заданными значениями.
- Пример создания матрицы из нулей:
A = zeros(3,4); % Создаём матрицу 3x4, заполненную нулями
A = ones(2,5); % Создаём матрицу 2x5, заполненную единицами
Эти методы позволяют вам гибко работать с матрицами, изменяя их размер в процессе вычислений.
Реализация операций сложения и умножения матриц
В MATLAB для выполнения операций сложения и умножения матриц используются стандартные операторы: «+» для сложения и «*» для умножения. Важно помнить, что для корректного выполнения операций должны быть выполнены условия совместимости размерностей матриц.
Сложение матриц: Операция сложения возможна только для матриц одинакового размера. Если A и B – матрицы размером m x n, то их сумма C будет также иметь размер m x n, и каждый элемент C(i, j) вычисляется как сумма соответствующих элементов A(i, j) и B(i, j):
C(i, j) = A(i, j) + B(i, j).
Пример в MATLAB:
A = [1 2; 3 4];
B = [5 6; 7 8];
C = A + B;
Умножение матриц: Операция умножения матриц требует соблюдения правила совместимости размерностей. Если A – матрица размером m x n, а B – матрица размером n x p, то результатом умножения будет матрица C размером m x p. Каждый элемент C(i, j) вычисляется как скалярное произведение i-й строки матрицы A и j-го столбца матрицы B:
C(i, j) = A(i, 1)*B(1, j) + A(i, 2)*B(2, j) + … + A(i, n)*B(n, j).
Пример в MATLAB:
A = [1 2; 3 4];
B = [5 6; 7 8];
C = A * B;
Для удобства работы с большими матрицами MATLAB предоставляет встроенные функции, такие как sum для суммирования элементов матрицы и mtimes для умножения. Однако, оператор «*» идеально подходит для умножения двух матриц, а оператор «+» – для сложения, так как они автоматически проверяют размерности.
Матричное умножение и элементное умножение: Важно отличать обычное умножение матриц (с использованием «*») от элементного умножения (с использованием «.*»). Элементное умножение выполняется поэлементно, то есть каждый элемент одной матрицы умножается на соответствующий элемент другой матрицы. Для этого обе матрицы должны быть одинакового размера.
Пример элементного умножения в MATLAB:
A = [1 2; 3 4];
B = [5 6; 7 8];
C = A .* B;
Работа с элементами матрицы: индексация и изменения значений
Индексация в MATLAB осуществляется через скобки, где указываются строки и столбцы матрицы. В отличие от некоторых других языков программирования, индексация в MATLAB начинается с единицы. То есть первый элемент находится в позиции (1, 1), второй – в позиции (1, 2) и так далее.
Для обращения к элементу матрицы достаточно указать его индексы через запятую, например, A(2, 3) вернёт элемент, находящийся на второй строке и третьем столбце матрицы A.
Можно работать не только с одиночными элементами, но и с целыми строками или столбцами. Например, A(2, :) выберет вторую строку матрицы, а A(:, 3) – третий столбец.
Для изменения значения элемента достаточно присвоить новое значение. Например, команда A(2, 3) = 5; изменит значение элемента во второй строке и третьем столбце на 5. Если вы хотите изменить всю строку или столбец, указывайте двоеточие в соответствующей позиции. Например, A(2, :) = [1, 2, 3]; заменит всю вторую строку на заданные значения.
Если необходимо изменить несколько элементов матрицы одновременно, можно использовать диапазоны индексов. Например, A(1:3, 2:4) выберет подматрицу с первой по третью строку и со второго по четвёртый столбец, а затем вы можете изменить все её элементы, присвоив новое значение.
MATLAB поддерживает логическую индексацию. Например, для замены всех значений, больших 10, на 0, можно использовать условие: A(A > 10) = 0;. Это эффективный способ манипуляций с матрицей, когда вам нужно выполнить операции на основе условий.
Помимо этого, можно изменять элементы матрицы с использованием индексов, созданных векторы. Например, для замены значений в определённых строках или столбцах можно создать вектор индексов: rows = [1, 3, 5]; и затем выполнить замену: A(rows, :) = 0;, что заменит все значения в указанных строках на нули.
Как выполнить транспонирование матрицы в MATLAB
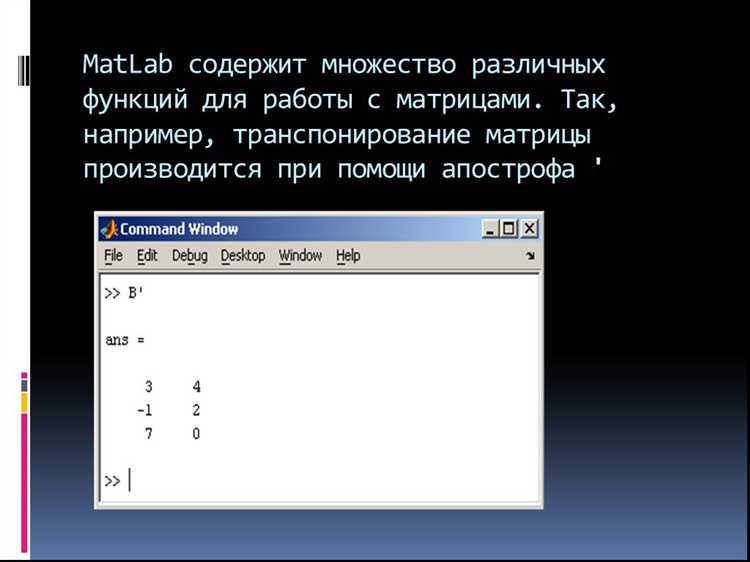
Транспонирование матрицы в MATLAB выполняется с помощью оператора апострофа (‘) или функции transpose(). Этот процесс заключается в замене строк на столбцы и наоборот.
Простейший способ транспонирования матрицы – использование оператора апострофа. Например, если у вас есть матрица A, то для её транспонирования достаточно ввести:
A_transposed = A';При этом результат будет новым массивом, в котором строки исходной матрицы станут столбцами, а столбцы – строками.
Также можно воспользоваться функцией transpose(), которая работает аналогично:
A_transposed = transpose(A);Оба способа дают одинаковый результат, но использование функции transpose() может быть предпочтительнее, если необходимо явно указать, что вы работаете с операцией транспонирования, а не с просто синтаксической записью.
Пример транспонирования матрицы:
A = [1, 2, 3; 4, 5, 6];
A_transposed = A'; % Результат: [1, 4; 2, 5; 3, 6]
Если матрица содержит комплексные числа, то при транспонировании будет выполнено также сопряжение, то есть знак мнимой части будет изменён. Для обычного транспонирования без сопряжения можно использовать функцию .' (точка апостроф):
A_transposed_no_conjugate = A.';
В случае работы с большими матрицами важно помнить, что транспонирование – это относительно дешёвая операция в MATLAB, но она может занять некоторое время при работе с огромными массивами данных.
Методы сохранения и экспорта матриц в MATLAB
В MATLAB существует несколько способов сохранения и экспорта матриц в различные форматы. Каждый метод зависит от того, как вы планируете использовать эти данные впоследствии.
1. Сохранение в бинарный файл с использованием функции save
Для сохранения переменных MATLAB в бинарный файл используется команда save. Этот метод позволяет сохранить матрицу или набор переменных в формате MATLAB (.mat), что идеально подходит для дальнейшего использования в среде MATLAB. Пример команды:
save('myMatrix.mat', 'A');Здесь 'myMatrix.mat' – это имя файла, а 'A' – имя переменной, которую вы хотите сохранить. Чтобы сохранить все переменные в рабочем пространстве, можно использовать команду:
save('allVariables.mat');2. Экспорт в текстовые файлы: save с параметром -ascii
Если требуется сохранить данные в текстовом формате, например, в виде числовых данных без меток, можно использовать параметр -ascii:
save('matrix.txt', 'A', '-ascii');Этот метод сохраняет матрицу как текстовый файл с числами, разделенными пробелами или табуляцией, что позволяет легко использовать его в других приложениях.
3. Экспорт в CSV формат с использованием writematrix
Для сохранения матрицы в формате CSV, который может быть открыт в большинстве таблиц и текстовых редакторов, рекомендуется использовать команду writematrix. Этот метод полезен, если требуется обмениваться данными с другими программами, такими как Excel:
writematrix(A, 'matrix.csv');Матрица будет сохранена как CSV файл, где каждый элемент разделяется запятой.
4. Экспорт в Excel с использованием writetable или xlswrite
Для экспорта данных в Excel можно использовать функцию writetable (если данные представлены в виде таблицы) или устаревшую xlswrite, которая также поддерживает экспорт матриц:
xlswrite('matrix.xlsx', A);Однако writetable подходит для более сложных структур данных, таких как таблицы с именами столбцов и строк.
5. Экспорт в текстовый файл с разделителями с помощью fprintf
fid = fopen('matrix.txt', 'w');
for i = 1:size(A, 1)
fprintf(fid, '%f\t', A(i, :));
fprintf(fid, '\n');
end
fclose(fid);6. Экспорт в другие форматы через MATLAB API
Для более сложных задач экспорта можно использовать MATLAB API для создания собственных скриптов, которые будут записывать данные в форматах, поддерживаемых другими приложениями (например, HDF5, JSON и другие).
Таким образом, MATLAB предоставляет широкий набор инструментов для сохранения и экспорта матриц в различных форматах в зависимости от ваших нужд и дальнейшего использования данных.