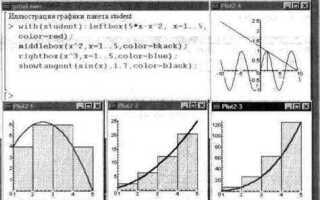
Как строить графики в maple

Maple – это мощная математическая среда, широко используемая для решения задач, связанных с анализом данных, математическим моделированием и визуализацией. Для построения графиков в Maple доступны различные подходы, позволяющие эффективно работать с функциями, системами уравнений и даже трехмерной графикой. Важно понимать, как выбирать нужный метод в зависимости от конкретной задачи, чтобы результат был максимально информативным.

Для построения графиков функций в Maple часто используется команда plot. Это основной инструмент для отображения двумерных графиков. Например, для графика функции f(x) = sin(x) достаточно ввести команду plot(sin(x), x = -Pi .. Pi). При этом можно задавать область отображения, масштабирование осей и добавлять дополнительные элементы, такие как сетка или легенда, через параметры команды. Чтобы добиться более точного отображения графика, полезно использовать высокое количество точек для интерполяции.

Для построения графиков нескольких функций на одном полотне можно воспользоваться командой plot[tools], которая позволяет комбинировать несколько функций в одном графике. Важно, чтобы функции были одного типа (например, все двумерные), иначе будет сложно правильно интерпретировать данные. С использованием параметра style можно настраивать визуальные особенности, такие как цвет, тип линии и маркеры для различных функций.

Для работы с трехмерными графиками в Maple предусмотрена команда plot3d, которая позволяет строить графики функций трех переменных или графики поверхностей. Синтаксис команды требует указания функции и диапазонов для всех трех переменных. Например, для отображения поверхности f(x, y) = x^2 + y^2 используйте команду plot3d(x^2 + y^2, x = -5 .. 5, y = -5 .. 5).

Использование Maple для построения графиков позволяет не только визуализировать данные, но и анализировать поведение функций при изменении параметров, что особенно полезно при решении сложных задач в области науки и инженерии.

Подготовка данных для графиков в Maple: импорт и обработка

Перед построением графиков в Maple необходимо правильно подготовить данные. Первый этап – импорт данных из различных источников, таких как текстовые файлы, Excel, базы данных и другие внешние ресурсы. Maple поддерживает несколько методов импорта: команду `Import` для текстовых файлов или интеграцию с Excel через пакет `ExcelTools`. Важно убедиться, что данные правильно отформатированы, чтобы избежать ошибок при обработке.

Для работы с текстовыми файлами можно использовать функцию `Import(«путь_к_файлу»)`. Она автоматически определяет структуру данных и преобразует их в удобный формат для дальнейших вычислений. Однако если структура данных сложная, требуется предварительная обработка. В случае использования Excel-файлов следует подключить пакет `ExcelTools`, а затем загрузить данные с помощью команды `ExcelTools:-Import(«путь_к_файлу»)`. При этом можно указать диапазоны ячеек и листы для точной настройки импорта.

После импорта важно выполнить очистку данных. Это включает в себя удаление пропусков, проверку на ошибки и приведение значений к необходимому типу. Для удаления пропусков используется функция `ListTools:-RemoveMissing()`, которая убирает все пустые элементы в списке. Также полезно использовать команды для поиска аномальных данных, например, `Statistics:-OutlierTest()` для выявления выбросов.

Если данные содержат текстовые значения, их необходимо привести к числовому виду. Maple позволяет преобразовывать строки в числа с помощью функции `parse`. Важно учесть единицы измерений, если они присутствуют в данных, и привести их к одной системе единиц для корректных расчетов и графиков.

Когда данные подготовлены, их можно структурировать в виде списков, массивов или таблиц. Для однотипных данных удобнее использовать списки, для многомерных массивов – структуры типа матрица. Списки в Maple имеют гибкость, позволяя работать с неравномерно распределёнными данными, тогда как матрицы удобны для работы с данными, которые представляют собой регулярные сетки, например, для графиков функции по двум осям.

На следующем этапе можно выполнять агрегацию или преобразования данных, такие как интерполяция или сглаживание. Maple предоставляет функции для этих операций, например, `Interpolation` для интерполяции данных между точками и `Spline` для сглаживания. Если требуется построение графиков с большими объёмами данных, можно также применить методы уменьшения размерности, такие как PCA, для упрощения представления данных.

Подготовка данных в Maple – это важный шаг для получения точных и информативных графиков. Правильный импорт, очистка и обработка данных позволяют избежать ошибок и значительно ускорить процесс визуализации.

Построение 2D графиков для функций: базовые приёмы

Для построения 2D графиков в Maple используется команда plot, которая позволяет отображать функции на плоскости с возможностью настройки параметров графика.

Пример базового построения графика функции:

plot(f(x), x = a..b);

Где f(x) – это выражение функции, а a..b задает диапазон по оси X.

Важные моменты при построении графиков:

Множество функций: можно строить несколько функций на одном графике, передав их через запятую в команду plot.

plot([f1(x), f2(x)], x = a..b);

Настройка стиля линии: для изменения стиля графика используйте параметр style. Например, можно построить график в виде точек или пунктирной линии.

plot(f(x), x = a..b, style = point);

Цвет линии: задается с помощью параметра color. Можно использовать стандартные цвета или задавать RGB-коды.

plot(f(x), x = a..b, color = red);

Ограничение области: для улучшения читаемости графика важно ограничивать область отображения. Убедитесь, что оси X и Y отображаются в нужных пределах.

plot(f(x), x = -10..10, y = -5..5);

Также можно использовать параметры title, xlabel и ylabel для добавления заголовков и подписей осей:

plot(f(x), x = a..b, title = "График функции", xlabel = "X", ylabel = "f(X)");

Для работы с графиками нескольких функций в одном окне можно использовать команду display, которая позволяет комбинировать несколько графиков:

display([plot1, plot2]);

Кроме того, Maple предоставляет функцию implicitplot для отображения графиков неявных функций, например, уравнений в виде f(x, y) = 0.

Создание 3D графиков для визуализации многомерных данных

Для работы с многомерными данными в Maple важно использовать 3D графики, которые позволяют наглядно представить взаимосвязь между несколькими переменными. Это особенно полезно при анализе данных с тремя и более измерениями. В Maple для создания 3D графиков можно использовать несколько подходов, включая графики поверхности, графики точек и графики векторных полей.

Основной командой для построения 3D графиков является plot3d. Рассмотрим ключевые параметры, которые могут быть полезны при построении таких графиков:

plot3d(f, x = a..b, y = c..d) – где f – функция, отображаемая в 3D пространстве, а x и y – диапазоны значений для осей.
axes = boxed – включает отображение осей в виде коробки.
view = [xmin..xmax, ymin..ymax, zmin..zmax] – позволяет задать диапазон отображаемых данных по осям X, Y и Z.
style = surface – задает стиль графика как поверхность, что позволяет визуализировать функции двух переменных.

Пример создания простого графика функции двух переменных:

plot3d(x^2 + y^2, x = -5..5, y = -5..5, style = surface, axes = boxed);

Если требуется отобразить точки в 3D пространстве, можно использовать команду pointplot3d. В этом случае важно учитывать формат входных данных. Например, для визуализации набора точек из массива данных можно использовать следующий код:

pointplot3d([[1, 2, 3], [4, 5, 6], [7, 8, 9]], style = point, symbol = solidcircle);

Для визуализации векторных полей можно использовать команду fieldplot3d, которая позволяет отобразить векторы, определённые в каждой точке 3D пространства:

fieldplot3d([sin(x)*cos(y), cos(x)*sin(y), x + y], x = -5..5, y = -5..5, z = -5..5);

При построении 3D графиков также стоит обратить внимание на следующие моменты:

Оптимизация производительности при больших объёмах данных. Для этого можно использовать параметр grid = 30 для задания числа точек на сетке, что позволит контролировать разрешение графика.
Применение цветовых схем для лучшего восприятия. В Maple можно использовать параметр color = color, чтобы задать цвет поверхности или точек, что помогает выделить ключевые области данных.
Использование анимации для динамической визуализации данных. Это можно сделать с помощью функции animate, которая позволяет отображать изменения данных во времени.

Таким образом, создание 3D графиков в Maple является мощным инструментом для анализа и визуализации многомерных данных. Используя различные стили и параметры, можно настраивать графики под конкретные задачи и получать точное представление о сложных взаимосвязях между переменными.

Настройка цветов и стилей линий для улучшения читаемости графиков

Цвет и стиль линий играют важную роль в восприятии графиков, особенно когда на одном графике отображается несколько функций. Правильный выбор параметров позволяет улучшить читаемость и облегчить анализ данных. Рассмотрим, как эффективно настроить эти элементы в Maple.

Maple предоставляет возможность изменять как цвет, так и стиль линий через параметры команд plot и plot[tools]. Вот несколько рекомендаций по их использованию:

1. Цвета

Для выделения различных графиков или элементов можно использовать яркие контрастные цвета. Однако важно помнить, что слишком много ярких оттенков может сделать график перегруженным. Рекомендуется выбирать цвета с учетом контекста, например, для функций, зависящих от времени, часто используют синие или зеленые оттенки, а для осей – более нейтральные цвета.

Пример настройки цвета линии функции:

plot([sin(x), cos(x)], x = -Pi .. Pi, color = ["blue", "red"])

Для достижения лучшего визуального эффекта рекомендуется использовать следующие цвета:

Для положительных значений: синий, зеленый, пурпурный.
Для отрицательных значений: оранжевый, красный, желтый.
Для осей: серый или черный, чтобы не отвлекать от графика.

2. Стиль линий

Чтобы график был не только читаемым, но и эстетичным, можно изменить стиль линии. Maple позволяет выбрать различные стили: сплошная линия, пунктирная, тире-точка и другие. Важно, чтобы выбранный стиль соответствовал числу отображаемых данных и не путал пользователя.

Пример использования различных стилей линий:

plot([sin(x), cos(x)], x = -Pi .. Pi, linestyle = [solid, dash])

Рекомендуется использовать сплошные линии для основных графиков и пунктирные или тире-точка для вспомогательных. Такой подход помогает разделить важные данные от менее значимых.

3. Толщина линий

Управление толщиной линии помогает выделить наиболее важные элементы графика. Для ключевых графиков стоит использовать более толстые линии, а для второстепенных – тонкие. Maple позволяет задать толщину через параметр thickness.

Пример настройки толщины линии:

plot([sin(x), cos(x)], x = -Pi .. Pi, thickness = [2, 1])

4. Прозрачность

Использование прозрачности линий помогает избежать «перегрузки» графика при наложении нескольких графиков. Для этого параметра можно настроить значение прозрачности через параметр opacity.

Пример настройки прозрачности:

plot([sin(x), cos(x)], x = -Pi .. Pi, opacity = [0.5, 0.7])

5. Комбинированные настройки

Иногда имеет смысл комбинировать все вышеперечисленные параметры. Например, для отображения нескольких графиков с разными стилями и цветами, а также с измененной толщиной линий и прозрачностью, можно использовать следующую конструкцию:

plot([sin(x), cos(x)], x = -Pi .. Pi, color = ["blue", "red"], linestyle = [solid, dash], thickness = [2, 1], opacity = [0.8, 0.6])

Это позволяет сделать график более понятным и привлекательным, минимизируя визуальный шум и улучшая восприятие информации.

Заключение

Настройка цветов и стилей линий в Maple – это мощный инструмент для улучшения восприятия графиков. Важно подбирать параметры, ориентируясь на контекст задачи, чтобы данные были представлены ясно и эффективно. Правильный выбор цвета, стиля линии и других настроек позволяет избежать путаницы и сделать графики более информативными.

Использование анимаций в графиках для динамических процессов

Анимация графиков в Maple позволяет эффективно визуализировать динамические изменения, что особенно полезно для моделирования процессов во времени. Это значительно улучшает восприятие данных, позволяя наблюдать, как система изменяется при различных условиях. Анимации могут быть использованы для демонстрации таких процессов, как движение частиц, изменение кривых, колебания, динамика населения и т.д.

Для создания анимации в Maple применяется команда animate. Она позволяет строить графики, где данные обновляются на каждом шаге, создавая иллюзию движения. Например, для анимации кривой функции, изменяющейся во времени, можно использовать следующий код:


animate(plot, [f(x,t), x = -10..10], t = 0..2*Pi);

В данном примере функция f(x,t) будет строиться в зависимости от времени t, и график будет обновляться на каждом шаге. Рекомендуется использовать разумный диапазон для параметра времени, чтобы график не стал перегруженным или слишком быстрым.

Анимации особенно полезны для визуализации фазовых портретов или решений дифференциальных уравнений. Например, при решении системы уравнений, которая моделирует движение двух тел, можно использовать анимацию для отображения путей тел в пространстве:


animate(phaseportrait, [sys], t = 0..5);

Для улучшения восприятия анимации важно контролировать скорость изменений, чтобы она соответствовала реальной динамике процесса. Maple позволяет задавать частоту кадров и скорость анимации с помощью параметров frames и fps (frames per second). Чем больше частота кадров, тем плавнее будет анимация, но это также увеличивает нагрузку на процессор, особенно при сложных моделях.

Кроме того, можно комбинировать анимацию с другими средствами визуализации, например, с добавлением цветовых градиентов или 3D-графиков. Это делает анимации не только информативными, но и более наглядными. В случае с трехмерными графиками можно использовать анимации для отображения изменений в поверхности или объеме:


animate(plots[3dplot], [f(x,y,t), x=-5..5, y=-5..5], t=0..2*Pi);

Также стоит отметить, что анимации можно использовать не только для графиков, но и для отображения решений систем уравнений, процессов с обратной связью, моделей с различными параметрами, что позволяет исследовать и визуализировать их поведение в реальном времени.

Построение графиков для статистических данных: гистограммы и диаграммы рассеяния

Для визуализации статистических данных в Maple можно использовать два основных типа графиков: гистограммы и диаграммы рассеяния. Эти графики помогают понять распределение данных, выявить тенденции и аномалии, а также оценить зависимость между переменными.

Гистограмма – это график, который показывает распределение данных по интервалам. В Maple для построения гистограммы используется команда histogram. Гистограмма особенно полезна, когда необходимо увидеть, как часто данные встречаются в различных диапазонах. Чтобы построить гистограмму для набора данных, нужно выполнить следующий код:

data := [1, 2, 2, 3, 4, 5, 5, 5, 6, 7, 8, 9, 9, 9, 10];
histogram(data, bins=5);

В этом примере создается гистограмма с 5 интервалами. Можно настроить количество интервалов с помощью параметра bins или задать конкретные границы интервалов. Гистограмма помогает наглядно оценить, как распределены данные и какие диапазоны имеют наибольшую плотность значений.

Для анализа взаимосвязи между двумя переменными используется диаграмма рассеяния. Она помогает выявить корреляцию между данными. В Maple для этого используется команда pointplot. Рассмотрим пример, когда нужно построить диаграмму рассеяния для двух наборов данных:

x := [1, 2, 3, 4, 5];
y := [2, 3, 5, 7, 11];
pointplot([x, y]);

Диаграмма рассеяния покажет, как значения x соотносятся с значениями y. Важно отметить, что диаграмма рассеяния помогает не только в визуализации зависимости, но и в обнаружении выбросов или нелинейных связей. Можно добавить линию тренда, чтобы более точно оценить связь между переменными:

pointplot([x, y], style=point, color=blue);
linearFit := leastSquares([x, y]);
plot(linearFit, x=-1..6);

Здесь используется метод наименьших квадратов для нахождения линии тренда, которая добавляется к диаграмме рассеяния. Такой подход позволяет выявить линейную зависимость между переменными и оценить, насколько хорошо модель описывает данные.

Гистограммы и диаграммы рассеяния – важные инструменты для статистического анализа. В Maple можно гибко настроить их параметры и использовать дополнительные функции для более глубокого анализа данных, включая расчет корреляции или создание сложных графиков с несколькими наборами данных.

Экспорт графиков в различные форматы для презентаций и отчётов

В Maple доступен широкий спектр форматов для экспорта графиков, что позволяет интегрировать их в отчёты и презентации с учетом специфики задачи. Основные форматы включают векторные (например, PDF, EPS) и растровые (например, PNG, JPEG) изображения. Каждый формат имеет свои особенности, которые стоит учитывать при подготовке графиков для печатных и цифровых документов.

PDF – один из лучших форматов для профессиональных отчетов. Он сохраняет высокое качество изображения и поддерживает масштабирование без потери резкости. В Maple график можно экспортировать в PDF с помощью команды exportplot, что гарантирует сохранение всех деталей, включая линии и текст, в точности, как они были созданы.

EPS (Encapsulated PostScript) идеально подходит для научных публикаций, так как позволяет интегрировать графику в редакторы текста, такие как LaTeX, без потери качества. Этот формат поддерживает векторное изображение, что важно для сохранения четкости при увеличении масштаба.

Для цифровых документов и презентаций, например, в PowerPoint или Word, часто используют растровые форматы, такие как PNG и JPEG. Формат PNG предпочтителен, когда нужно сохранить прозрачный фон или добиться высокого качества изображения без потери данных при сжатию. JPEG, в свою очередь, больше подходит для изображений с большим количеством цветов, где не требуется высокая точность на деталях.

Для экспорта графиков в эти форматы в Maple используется команда exportplot, которая позволяет выбрать нужный формат и настройки качества. Простой пример команды для экспорта графика в PNG:

exportplot(plot, "plot.png", format="PNG");

Важно помнить, что при работе с графиками в Maple необходимо учитывать разрешение. Для презентаций и печатных материалов стоит выбирать разрешение не ниже 300 dpi, что гарантирует отличное качество изображения на больших экранах или при печати на бумаге.

Кроме того, Maple позволяет интегрировать графики прямо в документы в формате LaTeX с использованием команд типа plots[export], что удобно для создания научных отчётов, где требуется высокая точность отображения данных и формул.

Подводя итог, выбор формата зависит от конечной цели и платформы, на которой будет отображаться графика. Векторные форматы подходят для научных и технических публикаций, а растровые – для презентаций и онлайн-отчётов.