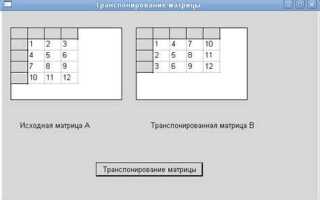
Транспонирование матрицы – это операция, при которой строки исходной матрицы превращаются в её столбцы. В системе Maple эта операция выполняется с помощью встроенной функции Transpose, которая позволяет не только инвертировать матрицу, но и легко работать с большими и сложными вычислениями.
Для того чтобы транспонировать матрицу, достаточно передать её в функцию Transpose. Например, для матрицы A транспонирование выглядит следующим образом:
A := Matrix([[1, 2], [3, 4]]); Transpose(A);
Maple автоматически изменит строки на столбцы, а результат будет отображён в виде новой матрицы. Если необходимо выполнить транспонирование сложных матриц или матриц с элементами разных типов (например, чисел и символов), Maple подстраивается под этот формат и корректно обработает такие данные.
Также стоит помнить, что транспонирование симметричной матрицы оставляет её без изменений. В случае, если вам нужно транспонировать более сложные объекты, такие как матрицы с параметрами или символами, Maple автоматически учтет это при выполнении операции, предоставив вам точный и корректный результат.
Создание матрицы в Maple для транспонирования

Для начала работы с матрицей в Maple, необходимо определить её с помощью команды Matrix. Это можно сделать, указав элементы матрицы в виде списка списков, где каждый внутренний список представляет строку матрицы. Например, для матрицы размером 2×3, можно использовать следующий синтаксис:
Matrix([[1, 2, 3], [4, 5, 6]])
При создании матрицы важно помнить, что элементы могут быть как числами, так и выражениями или переменными. Если вы хотите работать с переменными, например, x, y, можно задать матрицу следующим образом:
Matrix([[x, y], [y, x]])
После создания матрицы, чтобы транспонировать её, используйте команду Transpose. Она возвращает новую матрицу, где строки исходной матрицы становятся её столбцами:
Transpose(Matrix([[1, 2, 3], [4, 5, 6]]))
Этот код создаст транспонированную матрицу, которая будет выглядеть так:
[ [1, 4], [2, 5], [3, 6] ]
Важно помнить, что транспонированная матрица не изменяет исходную; она создаёт её новую версию. Maple позволяет работать с матрицами любых размеров, и для них эта операция будет выполняться по аналогии.
При работе с большими матрицами рекомендуется заранее проверять их размерность с помощью функции Dimension. Это полезно, чтобы избежать ошибок при транспонировании, так как транспонировать можно только прямоугольные или квадратные матрицы.
Dimension(Matrix([[1, 2], [3, 4]]))
Если исходная матрица представляет собой список списков, следует убедиться, что она корректно структурирована для использования команды Matrix и операций с ней.
Использование команды transpose для получения транспонированной матрицы

В Maple команда transpose позволяет легко и быстро получить транспонированную матрицу, меняя местами строки и столбцы исходной матрицы. Для выполнения операции транспонирования достаточно передать матрицу в качестве аргумента функции. Например, если у вас есть матрица A, транспонированную матрицу можно получить с помощью transpose(A).
Пример использования:
A := Matrix([[1, 2, 3], [4, 5, 6]]);
transpose(A);
После выполнения этой команды, результатом будет следующая транспонированная матрица:
[[1, 4], [2, 5], [3, 6]]
Особенность команды заключается в том, что она автоматически определяет размеры матрицы и корректно меняет местами строки и столбцы, независимо от их количества. Если исходная матрица является квадратной, транспонированная матрица также будет квадратной, но с изменёнными элементами на диагонали.
Для матрицы с произвольным размером команда transpose меняет количество строк и столбцов местами. Например, если исходная матрица имеет размерность 2×3, транспонированная будет иметь размерность 3×2.
Использование команды transpose в Maple не требует предварительных манипуляций с размерностью матрицы. Она автоматически обрабатывает различные типы матриц, включая матрицы с различным числом строк и столбцов. При этом важно помнить, что команда работает исключительно с матрицами, а не с другими типами объектов, такими как списки или векторы, что может потребовать дополнительных преобразований.
Как транспонировать подматрицы в Maple

Для транспонирования подматриц в Maple необходимо сначала выделить нужную подматрицу из исходной матрицы, а затем применить операцию транспонирования к выбранному фрагменту. В Maple подматрицу можно выделить с помощью оператора индексации, который позволяет выбрать определённые строки и столбцы.
Предположим, у вас есть матрица A размера 4×4:
A := Matrix([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12], [13, 14, 15, 16]]);
Чтобы транспонировать подматрицу, например, из элементов во втором и третьем столбцах и третьей и четвёртой строках, используйте следующее выражение:
SubMatrix := A[3..4, 2..3]; TransposedSubMatrix := Transpose(SubMatrix);
Здесь A[3..4, 2..3] извлекает подматрицу из строк с индексами 3 и 4, и столбцов с индексами 2 и 3. Функция Transpose затем транспонирует эту подматрицу.
Также можно транспонировать подматрицу на месте без её явного сохранения. Для этого используйте операцию транспонирования непосредственно внутри индексации:
A[3..4, 2..3] := Transpose(A[3..4, 2..3]);
Эта команда сразу заменит исходную подматрицу её транспонированным вариантом. При необходимости можно транспонировать несколько подматриц одновременно, следуя аналогичной логике.
Решение проблемы транспонирования симметричных матриц
Транспонирование симметричной матрицы в Maple не требует дополнительных вычислений, поскольку для симметричных матриц операция транспонирования не изменяет её структуру. Симметричная матрица, по определению, удовлетворяет условию, что её элементы относительно главной диагонали одинаковы, то есть \( A[i,j] = A[j,i] \) для всех \( i \) и \( j \).
При транспонировании симметричной матрицы её элементы остаются на тех же позициях, поскольку они уже симметричны относительно диагонали. Это означает, что операцию транспонирования можно выполнять без изменений, что существенно снижает вычислительные затраты. В Maple для этого используется стандартная функция Transpose, которая возвращает саму матрицу, если она симметрична. Таким образом, трансформировать симметричную матрицу достаточно просто, и при этом не возникает необходимости в дополнительных проверках.
Однако в случае работы с большими симметричными матрицами, использование транспонирования может быть неэффективным, так как оно может привести к избыточным операциям. В таких случаях целесообразно напрямую работать с матрицей, не применяя операцию транспонирования, а только учитывать симметричность при дальнейших вычислениях.
Для проверки симметричности матрицы в Maple можно использовать выражение: is( A = Transpose(A) ), что проверит, является ли матрица симметричной. В случае, если это условие выполнено, можно исключить операцию транспонирования при дальнейших вычислениях, улучшая производительность программы.
Как избежать ошибок при транспонировании матриц в Maple
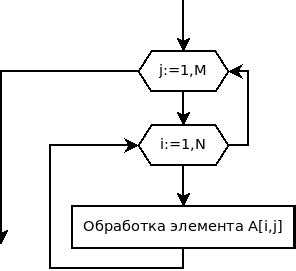
Для начала убедитесь, что ваша матрица правильно задана. В Maple транспонирование матрицы выполняется через команду `Transpose()`. Часто ошибка возникает, когда пытаются транспонировать объект, который не является матрицей (например, вектор или выражение). Пример правильного использования:
A := Matrix([[1, 2, 3], [4, 5, 6]]); B := Transpose(A);
Кроме того, важно помнить, что транспонированная матрица меняет строки на столбцы и наоборот. Это может вызвать недоразумения при работе с многомерными массивами. Перед транспонированием всегда проверяйте, что размерности вашей матрицы соответствуют ожидаемым.
Если вы работаете с большими матрицами или выполняете последовательные операции, следите за тем, чтобы тип данных оставался совместимым. Например, при попытке транспонировать матрицу, состоящую из символов или сложных выражений, может возникнуть ошибка. В таких случаях полезно сначала преобразовать все элементы в числовой формат или упростить выражения перед транспонированием.
Еще одной распространённой ошибкой является неучёт особенностей работы с матрицами, которые содержат нулевые строки или столбцы. После транспонирования такие строки или столбцы могут быть неверно интерпретированы или вызвать ошибку при дальнейших вычислениях. В таких случаях стоит предварительно удалить пустые строки или столбцы с помощью команды `DeleteRow()` или `DeleteColumn()`.
Не забывайте о специфике транспонирования симметричных матриц. В теории матрица будет оставаться неизменной, но важно удостовериться, что все элементы, включая диагональные, правильно обрабатываются в контексте численных вычислений в Maple.
Также полезно использовать команду `isMatrix()` для проверки, что объект является матрицей перед применением операции транспонирования. Это поможет избежать ошибок в случае случайной попытки транспонировать неправильный тип объекта.
Транспонирование матриц с фиксированными размерами и условиями
Для матрицы размера m × n, транспонированная матрица будет иметь размер n × m. Это необходимо учитывать при работе с фиксированными размерами, так как они могут быть использованы для оптимизации вычислений.
- Фиксированные размеры: При транспонировании матриц с известными размерами, например, 2×3 или 3×3, мы точно знаем, как изменятся индексы элементов. Например, если исходная матрица A имеет вид 2×3, то её транспонированная матрица A^T будет 3×2.
- Условия транспонирования: В случае фиксированных условий, например, при условии, что элементы матрицы ограничены определённым диапазоном или типом данных, важно учитывать, как транспонирование влияет на эти характеристики. Если элементы исходной матрицы содержат только числа, то транспонированная матрица будет содержать такие же числа, но расположенные по-другому.
- Преимущества: Использование фиксированных размеров позволяет избежать перерасчёта каждого элемента вручную. В Maple можно задать размерность матрицы заранее, что минимизирует вероятность ошибок при транспонировании.
В Maple транспонирование выполняется с помощью функции Transpose(). Для матрицы A размером m × n команда будет выглядеть так:
Transpose(A)
Пример:
A := Matrix([[1, 2, 3], [4, 5, 6]]);
Транспонированная матрица будет следующей:
Transpose(A)
- Рекомендации: Для матриц с фиксированными размерами рекомендуется заранее проверять их размерность перед выполнением транспонирования, чтобы избежать ошибок в дальнейшем. В случае работы с большими матрицами, можно использовать оператор транспонирования напрямую в вычислениях, что ускоряет процесс.
- Ограничения: Важно помнить, что транспонирование не изменяет саму структуру данных, а только меняет их представление. Поэтому для выполнения дальнейших операций, таких как умножение матриц, нужно учитывать новые размеры транспонированной матрицы.