Что понимают под символьными операциями в mathcad

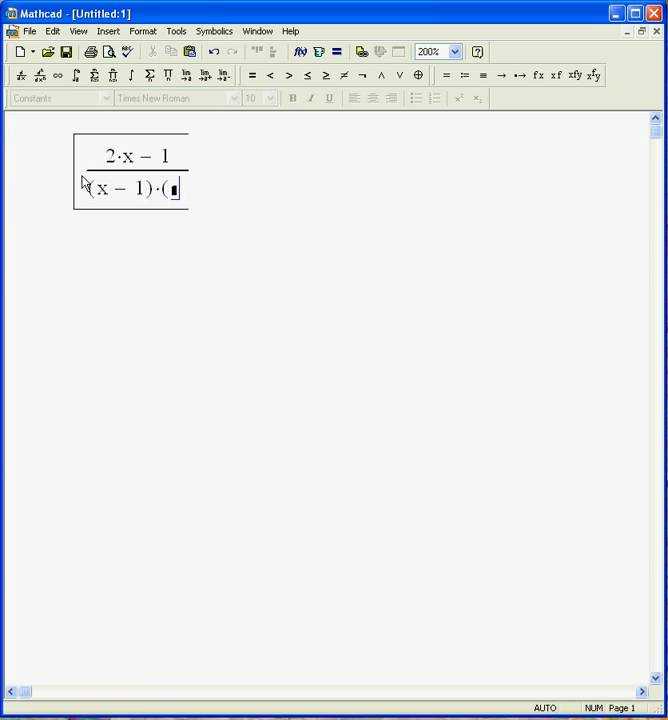
Mathcad предоставляет мощный инструментарий для работы с символьными выражениями, позволяя выполнять аналитические преобразования и получать точные решения без приближений. Основной задачей символьных операций является упрощение, дифференцирование, интегрирование и преобразование выражений в удобный для анализа вид.

Символьные вычисления в Mathcad реализуются с помощью встроенного движка CAS (Computer Algebra System), который поддерживает работу с алгебраическими, тригонометрическими и логарифмическими функциями, а также с выражениями, содержащими переменные и параметры. Это особенно важно при решении дифференциальных уравнений и оптимизационных задач, где аналитическое представление результатов повышает точность и облегчает последующую интерпретацию.

Для эффективной работы с символьными выражениями рекомендуется строго соблюдать правила определения переменных и избегать избыточных преобразований, которые могут привести к усложнению формул и снижению производительности расчетов. Встроенные функции Mathcad позволяют контролировать процесс упрощения и получать формулы, максимально пригодные для практического использования.

Символьные операции в Mathcad: назначение и применение

Основные функции включают упрощение выражений (simplify), разложение на множители (factor), дифференцирование (diff), интегрирование (int), вычисление пределов (limit) и преобразование выражений в разные формы (expand, collect). Каждая операция возвращает результат в виде символического выражения, удобного для дальнейшей аналитической работы.

Применение символьных операций эффективно в задачах алгебры, анализа, теории функций и инженерных расчетах, где необходима точность и сохранение математической структуры. Например, дифференцирование с помощью diff позволяет получить точную производную без численного шума, что важно при анализе функций с параметрами.

Для корректной работы с символьными выражениями следует использовать встроенный движок символических вычислений Mathcad (Maple или MuPAD, в зависимости от версии). Рекомендуется избегать смешивания численных и символьных переменных в одном выражении для предотвращения ошибок.

Практическая рекомендация – применять символьные операции на ранних этапах решения, чтобы получить общее аналитическое выражение, которое затем можно подставлять числовые значения для конкретных параметров. Это ускоряет многократные вычисления и облегчает проверку правильности формул.

Как использовать символьные выражения для упрощения математических формул

В Mathcad символьные выражения позволяют преобразовывать сложные формулы в более компактные и удобные для анализа формы. Для упрощения применяют функцию simplify(), которая автоматически сокращает выражения, объединяет подобные члены и раскрывает скобки, сохраняя математическую корректность.

Для конкретного выражения нужно задать переменные как символьные с помощью команды symbol() или при объявлении, чтобы Mathcad оперировал ими как символами, а не числовыми значениями. Это важно для корректной работы функций упрощения и преобразования.

Упрощение стоит применять поэтапно: сначала убрать скобки и привести подобные с помощью expand() и combine(), затем применить simplify() для оптимизации структуры. Такой подход обеспечивает более предсказуемый результат и позволяет контролировать промежуточные преобразования.

Для дробных выражений рекомендуется использовать simplify() совместно с функцией factor(), чтобы разложить числитель и знаменатель на множители, что помогает выявить и сократить общие делители. В результате формула становится короче и легче воспринимается.

Mathcad также поддерживает замены переменных и подстановки, что позволяет упростить выражения с помощью конкретных условий или дополнительных соотношений. Это особенно полезно для исключения лишних параметров и преобразования формул в более удобные для решения задачи виды.

Важный момент – использовать упрощение только после точного задания контекста задачи, чтобы избежать потери информации или нежелательных преобразований, особенно при работе с тригонометрическими, логарифмическими и экспоненциальными функциями.

Преобразование и факторизация многочленов в Mathcad

В Mathcad факторизация многочленов осуществляется с помощью функции factor(), которая раскладывает выражение на простейшие множители. Для применения необходимо задать многочлен как символьное выражение, используя оператор := и функцию symbol() для объявления переменной.

Пример: factor(x^3 - 3*x^2 + 3*x - 1) вернёт разложение на множители вида (x - 1)^3. Mathcad учитывает алгебраические свойства корней и позволяет работать с многочленами с параметрами и коэффициентами, представленными символически.

Преобразование выражений включает упрощение через simplify() и разложение с выделением общих множителей. Это важно для анализа корней, построения графиков и решения уравнений. Mathcad поддерживает как разложение над полем действительных чисел, так и с комплексными коэффициентами, что расширяет возможности факторизации.

Для многочленов с несколькими переменными функция factor() осуществляет частичную факторизацию по указанной переменной. Управлять процессом преобразования позволяет дополнительный параметр, задающий уровень упрощения.

Практическая рекомендация: всегда преобразуйте многочлен в символьный формат перед факторизацией, чтобы избежать ошибок числовой аппроксимации. Для больших выражений рекомендуется комбинировать expand() и factor() для контроля вида результата.

Mathcad эффективно интегрирует символьные операции с численными, что позволяет автоматически использовать факторизацию при вычислениях корней и интегралах многочленов, облегчая последующий анализ и интерпретацию результатов.

Решение уравнений с помощью символьных методов Mathcad

Mathcad предоставляет мощные инструменты для точного решения уравнений через символьные вычисления. Для уравнений алгебраической и трансцендентной природы применяется функция solve, позволяющая получать аналитические решения без численного приближения.

При задании уравнения необходимо использовать оператор равенства = в символьном контексте, например: solve(x^2 — 4 = 0, x). Mathcad автоматически распознает переменные и формирует аналитическое выражение корней.

Для систем уравнений доступна функция solve() с массивом уравнений и переменных. Mathcad возвращает вектор решений, упрощая работу с несколькими неизвестными одновременно. Рекомендуется предварительно проверять условия совместности и избегать неоднозначностей в обозначениях переменных.

Символьное решение позволяет применять дальнейшие преобразования: интегрирование, дифференцирование, упрощение выражений. Это значительно расширяет возможности анализа и оптимизации математических моделей без перехода к численным методам.

Особенно эффективна функция root() для поиска корней многочленов, где Mathcad строит точные формулы корней и упрощает их. Для уравнений более высокой степени предпочтительно использовать root() в сочетании с simplify() для компактного представления результата.

При работе с параметрическими уравнениями Mathcad позволяет вводить параметры как символьные переменные, что делает возможным исследование зависимости решений от параметров без многократного повторного вычисления.

Вычисление производных и интегралов символьно в Mathcad

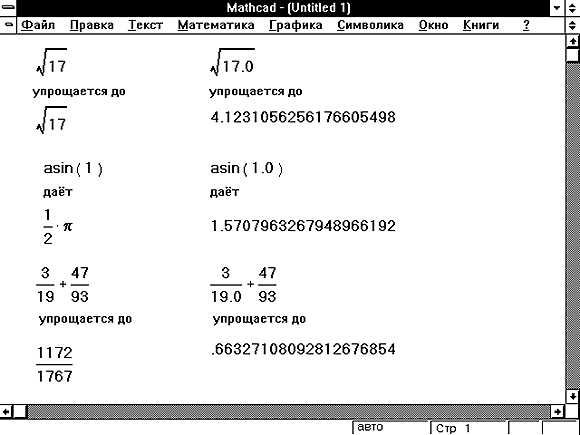
Mathcad позволяет выполнять символьное дифференцирование и интегрирование с высокой точностью и удобством. Основные операции строятся на использовании встроенных функций, работающих с выражениями в аналитическом виде.

• Символьное дифференцирование: для нахождения производной используется оператор d/dx или функция diff(). Формат: diff(выражение, переменная). Mathcad возвращает аналитическое выражение производной без численного приближения.
• Важна правильная постановка переменной дифференцирования – она должна быть объявлена символом, а не числом. Иначе результат будет некорректным.
• Для вычисления производной высших порядков добавляется третий параметр – порядок производной: diff(выражение, переменная, порядок).

• Символьное интегрирование: реализуется функцией int(). Синтаксис: int(выражение, переменная) для неопределенного интеграла.
• Определенный интеграл задается через дополнительные параметры: int(выражение, переменная, нижний_предел, верхний_предел). Mathcad возвращает аналитическое значение при возможности вычисления.
• При невозможности найти точное выражение интеграла Mathcad сигнализирует о необходимости численного интегрирования.

Рекомендации по работе:

1. Используйте символические переменные без заданных числовых значений, чтобы сохранить аналитичность результата.
2. Для сложных выражений полезно предварительно упростить их с помощью функции simplify() перед дифференцированием или интегрированием.
3. При вычислении определенных интегралов проверяйте корректность пределов – они должны быть числовыми значениями.
4. Для визуальной проверки результатов рекомендуется строить графики исходной функции и её производной или интеграла.

Символьные возможности Mathcad обеспечивают точный и удобный инструментарий для аналитического исследования функций без перехода к численным методам.

Подстановка и упрощение символьных выражений с параметрами

Для подстановки необходимо явно указать переменную и значение, которое её заменяет, что обеспечивает точный контроль над преобразованиями. Важно соблюдать тип данных при замене – числовые значения и символьные выражения требуют разного подхода, чтобы избежать ошибок интерпретации.

Упрощение символьных выражений происходит через встроенные процедуры упрощения (simplify), которые сокращают сложные формулы, сводят подобные члены и устраняют избыточные операции. Для параметрических выражений рекомендуется применять упрощение после подстановки, поскольку это снижает вычислительную нагрузку и улучшает читаемость результата.

Практически полезно использовать упрощение для выявления критических точек, граничных случаев и оптимизации формул в зависимости от параметров. Для контроля процесса упрощения можно включать или отключать отдельные правила преобразования, что позволяет добиться нужного уровня детализации в итоговом выражении.

Оптимальная последовательность работы: сначала подставить все известные параметры, затем выполнить упрощение. Такой подход минимизирует вероятность возникновения неопределённостей и повышает точность дальнейших вычислений и анализа.

Работа с матрицами и векторами в символьной форме Mathcad

Mathcad позволяет выполнять точные символьные операции с матрицами и векторами, что важно при аналитическом решении задач линейной алгебры и систем уравнений. Символьная обработка сохраняет выражения в общем виде без численных приближений, обеспечивая полное раскрытие структуры.

Основные возможности при работе с символьными матрицами и векторами:

• Объявление символьных матриц и векторов с использованием переменных и параметров, позволяющих задавать элементы через выражения.
• Выполнение операций сложения, вычитания и умножения с автоматическим упрощением результатов.
• Определение и вычисление детерминанта, обратной матрицы и ранга в символьном виде.
• Решение систем линейных уравнений с символьными коэффициентами через встроенные функции.
• Диагонализация матриц, нахождение собственных значений и собственных векторов без численного аппроксимирования.

Для эффективного использования символьных матриц рекомендуется:

1. Объявлять элементы матриц как символы или функции для максимальной гибкости при преобразованиях.
2. Использовать встроенную функцию det() для получения символьного выражения детерминанта без потери точности.
3. При вычислении обратной матрицы применять функцию inv(), обращая внимание на условие невырожденности.
4. Применять функцию eigenvals() для извлечения символических собственных значений, что облегчает анализ параметрических зависимостей.
5. Использовать функцию simplify() для сокращения сложных выражений, возникающих в результате операций.

Символьные векторы в Mathcad можно рассматривать как частный случай матриц с одной строкой или столбцом. Для них доступны те же операции и функции, что и для матриц, включая вычисление нормы, скалярного и векторного произведений с сохранением символической формы.

Понимание структуры символьных матриц и оптимальное применение встроенных функций Mathcad ускоряет работу с параметрическими задачами и способствует более глубокому аналитическому исследованию.

Преобразование выражений в числовой вид из символьного формата

В Mathcad для преобразования символьных выражений в числовые значения используется оператор evalf. Этот оператор применяют в случаях, когда необходимо получить численный результат после аналитических преобразований, таких как упрощение, разложение в ряд, дифференцирование или интегрирование.

Для применения evalf к выражению, его необходимо сначала преобразовать с использованием символического оператора = (не путать с :=), после чего результат можно численно оценить с помощью evalf или клавиши Ctrl+.. Например:

diff(sin(x), x) = выдаёт cos(x). Применяя evalf при x = π/4, получаем численное значение: cos(π/4) ≈ 0.7071.

Если требуется заменить символьные переменные на конкретные значения перед численным вычислением, используется подстановка: expr | x = a, после чего применяется evalf. Например:

ln(x^2 + 1) | x = 2 → evalf даст ln(5) ≈ 1.6094.

Важно учитывать точность: Mathcad по умолчанию использует ограниченное число значимых цифр, которое можно изменить через меню Tools → Worksheet Options → Result Format.

Для векторов и матриц evalf применяется к каждому элементу. Символьные элементы сначала упрощаются, затем преобразуются в числовую форму. Пример:

[sin(π/6), ln(e)] = [0.5, 1] при использовании evalf.

Не рекомендуется применять evalf к выражениям, содержащим неопределённости, такие как 0/0 или ∞ — ∞. В этих случаях предварительно необходимо упростить выражение или изменить область определения переменных.

Использование символьных вычислений для анализа функций и графиков

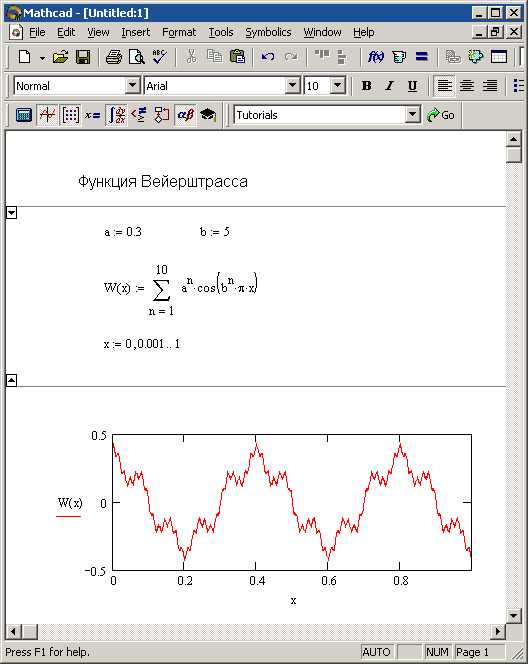
Mathcad позволяет находить аналитические выражения производных, интегралов и пределов функций, что критически важно для точного анализа их поведения. Например, при исследовании функции f(x) = x·sin(x) символьное дифференцирование с помощью оператора diff(f(x), x) мгновенно даёт результат sin(x) + x·cos(x), позволяя определить интервалы возрастания и убывания функции без численного приближения.

Для построения графиков с учётом особенностей функции важно точно определить критические точки. Команда solve(diff(f(x), x) = 0, x) возвращает аналитические значения, где производная обращается в ноль. Это упрощает определение максимумов и минимумов, что особенно полезно при работе с параметрическими или сложными функциями.

Символьное интегрирование позволяет точно определить площадь под графиком. Интеграл ∫x²·e^(-x) dx, вычисленный символьно через operator int(x²*exp(-x), x), выдаёт точное выражение, которое невозможно получить численно с гарантированной точностью.

При анализе асимптотического поведения функции использование символьных пределов через limit(f(x), x, ∞) выявляет тенденции роста или убывания. Это критично при построении графиков с бесконечными интервалами или при исследовании сходимости рядов.

Символьная подстановка выражений с помощью функции substitute позволяет трансформировать уравнения и системы перед дальнейшим анализом. Это удобно при анализе графиков, зависящих от нескольких параметров, когда требуется быстро подставить конкретные значения и оценить влияние параметров на форму кривой.

Вопрос-ответ:

Чем символьные операции в Mathcad отличаются от численных?

Символьные операции позволяют работать с выражениями как с формулами, а не с конкретными числами. Например, при символьном упрощении выражения Mathcad выдает общую форму результата, не подставляя значения переменных. В отличие от численных вычислений, символьные операции не требуют заранее заданных чисел и позволяют сохранять переменные в аналитическом виде. Это удобно при проверке общих свойств формул и упрощении выражений перед подстановкой значений.

Какие символьные функции доступны в Mathcad?

Mathcad предоставляет широкий набор символьных функций, включая упрощение выражений (`simplify`), взятие производных (`diff`), интегрирование (`int`), разложение в ряд Тейлора (`taylor`), преобразование выражений (`expand`, `factor`) и другие. Все эти функции позволяют преобразовывать математические выражения без подстановки конкретных значений. Их можно использовать при анализе формул, разработке алгоритмов и проверке корректности математических преобразований.

Можно ли использовать символьные операции при работе с уравнениями?

Да, Mathcad поддерживает символьное решение уравнений и систем уравнений. Для этого используется оператор `solve`, который позволяет получить решение в аналитическом виде. Это полезно, когда требуется общее решение задачи или когда нужно провести дальнейшие преобразования с найденным выражением. Также можно использовать операторы `lhs` и `rhs` для обращения к левой и правой части уравнения.

Есть ли ограничения при использовании символьных операций?

Да, у символьных операций есть некоторые ограничения. Во-первых, не все выражения можно преобразовать или упростить до удобного вида. Иногда результат может быть слишком громоздким или неожиданным. Во-вторых, не все численные функции имеют символьные аналоги. Также следует учитывать, что символьные операции требуют больше ресурсов и могут выполняться медленнее, особенно при работе со сложными выражениями.

В каких задачах символьные операции особенно полезны?

Символьные операции особенно полезны в тех случаях, когда требуется аналитическое представление решения: при выводе формул, проверке тождеств, упрощении выражений перед подстановкой чисел. Также они используются в учебных целях, при анализе зависимости переменных и при создании универсальных шаблонов расчетов. Например, в инженерных расчетах удобно сначала упростить выражение символьно, а затем провести численный расчет.