Команда NDSolve в Mathematica предназначена для численного решения дифференциальных уравнений, включая обыкновенные, с частными производными и системы уравнений. Основной результат – интерполирующая функция, которую можно использовать как обычную функцию в последующих вычислениях. Это позволяет избежать повторного решения задачи при каждом обращении к результату.
Для получения численного решения необходимо задать уравнение, граничные или начальные условия и диапазон переменных. Пример: NDSolve[{y'[x] == -2 y[x], y[0] == 1}, y, {x, 0, 5}]. Возвращается список с правилом, где y представлена в виде интерполяционной функции, доступной по записи y[x] /. %.
Результат NDSolve можно сразу использовать в построении графиков, численном дифференцировании или интегрировании. Например, Plot[y[x] /. sol, {x, 0, 5}] отобразит решение. Для повышения точности решения следует указывать параметры AccuracyGoal и PrecisionGoal. При работе с жёсткими уравнениями целесообразно использовать Method → «StiffnessSwitching».
Если требуется сохранить результат как независимую функцию, удобно определить: f[x_] := y[x] /. First@NDSolve[… ]. Это позволяет вызывать f[x] в любой точке диапазона без повторного вызова NDSolve, обеспечивая компактность и производительность вычислений.
Как задать систему дифференциальных уравнений для NDSolve
Для корректного использования NDSolve необходимо задать систему уравнений в виде списка. Каждое уравнение должно быть выражено через производные, используя y'[x] или y''[x] и т.д. Все переменные и их производные должны быть функциями от независимой переменной, чаще всего x или t.
- Используйте
==для обозначения равенства. Присваивание через=приведёт к ошибке. - Каждое уравнение и начальное условие должно быть элементом списка, заключённого в
{ }. - Имена функций должны быть уникальны. Например,
y1[x],y2[x], а не простоy[x]дважды. - Начальные условия должны включать и значение функции, и её производной (если порядок уравнения выше первого). Например:
y[0] == 1,y'[0] == 0.
Пример корректной системы для численного решения:
NDSolve[
{
y1'[t] == -y1[t] + y2[t],
y2'[t] == y1[t] - 2 y2[t],
y1[0] == 1,
y2[0] == 0
},
{y1, y2},
{t, 0, 10}
]
Рекомендуется:
- Проверять линейность и порядок уравнений –
NDSolveможет решить как жёсткие, так и нелинейные системы, но численно. - Указывать диапазон интегрирования явно. Например,
{t, 0, 10}. - Избегать неопределённых выражений, например, деления на
y[t]без гарантии, чтоy[t] ≠ 0.
Для более сложных систем допускается использование WhenEvent и Piecewise, но они должны быть правильно встроены в уравнения и совместимы с численным решением.
Формат записи начальных условий в NDSolve
В Mathematica начальные условия в NDSolve задаются в виде уравнений, определяющих значения функции и её производных в начальный момент времени. Правильная запись: y[0] == 1 для значения функции и y'[0] == 0 для производной. Условия указываются в одном списке с уравнением дифференциальной системы.
Например, для задачи второго порядка: y''[t] + y[t] == 0 с начальными условиями y[0] == 1 и y'[0] == 0, правильный вызов будет:
NDSolve[{y''[t] + y[t] == 0, y[0] == 1, y'[0] == 0}, y, {t, 0, 10}]Условия можно записывать в любом порядке относительно уравнения, но все элементы должны входить в общий список. Производные указываются с использованием апострофов или функции Derivative, например: Derivative[1][y][0] == 0 эквивалентно y'[0] == 0.
Для систем уравнений каждое начальное условие должно быть задано для каждой функции и каждой её производной до соответствующего порядка. Например, система из двух уравнений второго порядка требует четырёх начальных условий: по два на каждую функцию.
Если указано меньше условий, чем необходимо для порядка системы, NDSolve выдаст ошибку о недостатке начальных условий. Если условия заданы некорректно, например y[t == 0] == 1, будет синтаксическая ошибка. Убедитесь, что используется правильная форма: y[0] == 1.
Извлечение численной функции из результата NDSolve
После выполнения NDSolve в Mathematica результат возвращается в виде списка правил, например:
sol = NDSolve[{y''[x] + y[x] == 0, y[0] == 0, y'[0] == 1}, y, {x, 0, 10}];Для извлечения численного решения функции из результата необходимо использовать конструкцию с подстановкой:
ySol[x_] := y[x] /. First[sol]Функция First применяется для получения первого (и обычно единственного) правила из списка, возвращаемого NDSolve. Далее подстановка /. заменяет символическую функцию y[x] на численную интерполяцию.
Полученная функция ySol[x] может быть вызвана с любым значением аргумента внутри указанного диапазона. Для получения численного значения используется:
ySol[3.5]или с указанием точности:
N[ySol[π], 20]Если в системе несколько функций, используйте имена явно. Например:
sol = NDSolve[{y'[x] == z[x], z'[x] == -y[x], y[0] == 0, z[0] == 1}, {y, z}, {x, 0, 10}];ySol[x_] := y[x] /. First[sol]
zSol[x_] := z[x] /. First[sol]Для построения графиков используйте:
Plot[ySol[x], {x, 0, 10}]или несколько функций одновременно:
Plot[{ySol[x], zSol[x]}, {x, 0, 10}]Извлечённая функция сохраняет численные свойства: она недоступна в аналитическом виде и недопустима вне границ интегрирования. Проверяйте допустимость области через Domain или ручной контроль аргументов.
Построение графика полученной численной функции
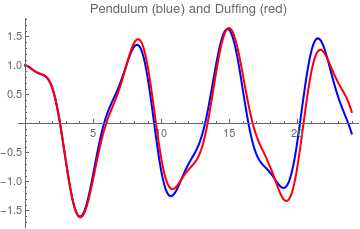
После получения численного решения с помощью NDSolve, результат обычно представляется в виде правила замены, например: {y[t] ⧴ InterpolatingFunction[{{0, 10}}, <>]}. Для визуализации этой функции используйте Plot, указав интервал определения интерполяционной функции.
Пример построения:
sol = NDSolve[{y»[t] + y[t] == 0, y[0] == 0, y'[0] == 1}, y, {t, 0, 10}];
Plot[y[t] /. sol, {t, 0, 10}]
Если в решении несколько функций, используйте Evaluate внутри Plot для повышения производительности:
Plot[Evaluate[{y[t], y'[t]} /. sol], {t, 0, 10}]
Проверьте, что переменная t находится в допустимом диапазоне интерполяционной функции. Выход за границы вызовет предупреждение или ошибку.
Для уточнения интервала используйте:
sol[[1, 1, 2, 1]] – начало интервала
sol[[1, 1, 2, 2]] – конец интервала
Если требуется отобразить несколько решений с различными начальными условиями, примените Table и Plot совместно:
sols = Table[NDSolve[{y»[t] + y[t] == 0, y[0] == 0, y'[0] == v}, y, {t, 0, 10}], {v, 0, 2, 0.5}];
Plot[Evaluate[Table[y[t] /. s, {s, sols}]], {t, 0, 10}]
Настройте оси и легенду при необходимости через PlotLegends и AxesLabel, чтобы повысить читаемость графика.
Работа с системой уравнений с несколькими переменными
Для решения системы дифференциальных уравнений с несколькими переменными в Mathematica с помощью NDSolve необходимо задать уравнения, начальные условия и переменные в виде списков. Все уравнения должны быть синтаксически корректными и однозначно определять производные всех искомых функций.
Пример: система двух уравнений с переменными x[t] и y[t]:
sol = NDSolve[
{
x'[t] == x[t] - y[t],
y'[t] == x[t] + y[t],
x[0] == 1,
y[0] == 0
},
{x, y},
{t, 0, 10}
]
Ключевым моментом является указание полного списка начальных условий – без них NDSolve не выполнит численное решение. Используйте Plot или ParametricPlot для визуализации результатов:
Plot[
Evaluate[{x[t], y[t]} /. sol],
{t, 0, 10},
PlotLegends -> {"x[t]", "y[t]"}
]
Для параметрического графика траектории:
ParametricPlot[
Evaluate[{x[t], y[t]} /. sol],
{t, 0, 10}
]
Если система жесткая, рекомендуется указать метод интегрирования явно, например, Method -> "StiffnessSwitching". Для анализа устойчивости или поведения при различных параметрах используйте Manipulate вместе с NDSolve внутри тела динамики.
Передача параметров в численное решение через NDSolve
Для передачи параметров в уравнения, решаемые с помощью NDSolve, рекомендуется использовать функциональный подход. Вместо подстановки числовых значений напрямую в уравнение, задайте уравнение как функцию от параметров. Это позволяет быстро изменять параметры без переписывания основной системы.
Например, система дифференциальных уравнений с параметром k оформляется так:
eqns[k_] := {y'[x] == k y[x], y[0] == 1}
Затем решение находится вызовом:
sol = NDSolve[eqns[2], y, {x, 0, 5}]
Такой способ упрощает исследование зависимости решений от параметров через автоматическую подстановку значений. Для более сложных систем с несколькими параметрами функция уравнений может принимать несколько аргументов.
Важно, чтобы параметры были числовыми при вызове NDSolve, иначе алгоритм выдаст ошибку. Чтобы избежать этого, в определении функции уравнений применяйте проверку типа или использование конструкции ?NumericQ в шаблонах параметров:
eqns[k_?NumericQ] := {...}
Это гарантирует, что NDSolve вызовет уравнение только с числовыми значениями параметров.
Если параметры используются внутри сложных выражений, лучше заранее вычислить их численные значения вне NDSolve, чтобы повысить эффективность и избежать неопределённостей в процессе численного решения.
При необходимости решения системы с несколькими наборами параметров удобно использовать Table или Map для генерации множества решений, например:
Table[NDSolve[eqns[k], y, {x, 0, 5}], {k, 1, 3, 0.5}]
Такой подход оптимизирует работу с параметрическими задачами и упрощает анализ результатов.
Вопрос-ответ:
Как можно использовать функцию NDSolve для получения численного решения обыкновенного дифференциального уравнения в Mathematica?
В Mathematica команда NDSolve позволяет получить приближенное численное решение дифференциальных уравнений. Для этого задают уравнение, начальные или граничные условия, а также переменную, по которой производится решение. В результате NDSolve возвращает интерполирующую функцию, которую можно применять для вычисления значений решения в конкретных точках. Например, для уравнения y'(x) = -y(x) с начальным условием y(0) = 1 вызов NDSolve[{y'[x] == -y[x], y[0] == 1}, y, {x, 0, 5}] создаст численное представление функции y на интервале от 0 до 5.
Можно ли с помощью NDSolve получить решение в виде явной функции, пригодной для дальнейших вычислений и построения графиков?
Да, NDSolve возвращает решение в форме интерполирующей функции, которую можно присвоить переменной и использовать для вычислений в произвольных точках из заданного диапазона. Например, если результат сохранить как sol = NDSolve[…, y, {x, a, b}], то извлечь функцию y можно через yFunc = y /. First[sol]. После этого yFunc[значение] даст численное значение решения в этой точке. Это удобно для построения графиков, анализа и интегрирования.
Как правильно задать начальные условия в NDSolve для задачи Коши с системой уравнений?
Для системы уравнений в NDSolve нужно указать каждое уравнение вместе с соответствующими начальными условиями. Например, для системы y1′(x) = f1(…), y2′(x) = f2(…), начальные условия задаются как y1[x0] == y10 и y2[x0] == y20, где x0 — начальная точка. В NDSolve это записывается списком: NDSolve[{уравнения, начальные условия}, {y1, y2}, {x, x0, x1}]. Это позволяет решить систему численно в указанном интервале.
Какие ограничения существуют при использовании NDSolve для жёстких уравнений или систем с резкими изменениями?
NDSolve хорошо справляется с широким классом уравнений, но при жёстких системах или уравнениях с резкими переходами решение может требовать настройки параметров метода. В таких случаях рекомендуется использовать опции Method, MaxStepSize, AccuracyGoal и PrecisionGoal, чтобы улучшить устойчивость и точность вычислений. Также можно попробовать специальные методы, например «StiffnessSwitching», которые адаптируются под сложность задачи.
Как извлечь и использовать численную функцию, полученную через NDSolve, для вычисления производных и интегралов?
Численное решение из NDSolve представляет собой интерполирующую функцию, которая поддерживает операции дифференцирования и интегрирования. Чтобы найти производную, достаточно применить оператор Derivative к функции, например D[yFunc[x], x]. Для интеграла можно использовать функцию NIntegrate, подставляя значения интерполированной функции в нужном диапазоне. Таким образом, полученную функцию удобно анализировать и применять для вычисления характеристик решения.