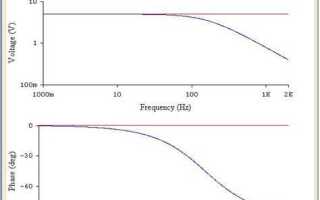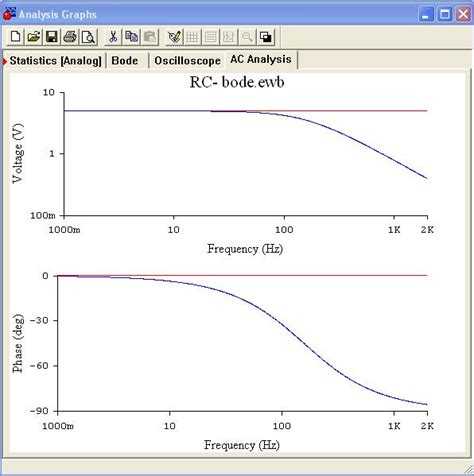
Платформа Mathcad предоставляет широкие возможности для анализа частотных характеристик линейных систем. Для построения амплитудно-частотной (АЧХ) и фазо-частотной характеристик (ФЧХ) достаточно определить передаточную функцию системы в виде отношения двух полиномов от комплексной переменной s = jω и использовать встроенные функции графического отображения.
Передаточная функция вводится как рациональное выражение, например: H(s) := (s + 10) / (s^2 + 3s + 2). Для перехода к частотной области замените s на j·ω, где ω – вектор частот, определённый через функцию linspace или range, например: ω := 0..100. Комплексное значение функции H(jω) позволяет получить модуль и фазу с помощью abs(H(jω)) и arg(H(jω)) соответственно.
Для отображения АЧХ используйте команду plot с логарифмической или линейной шкалой по оси частот. Преобразование модуля в децибелы выполняется выражением 20·log10(abs(H(jω))). Фазовая характеристика в градусах получается через arg(H(jω))·180/π. Убедитесь, что область частот охватывает интересующий диапазон и шаг дискретизации позволяет выявить резонансные пики и особенности фазы.
Для повышения точности анализа рекомендуется нормировать частотную ось относительно характерного частотного параметра системы (например, ω0 – собственная частота). Это позволяет интерпретировать поведение системы в относительных единицах и упрощает сравнение различных структур управления.
Импорт экспериментальных данных в Mathcad для построения АЧХ и ФЧХ
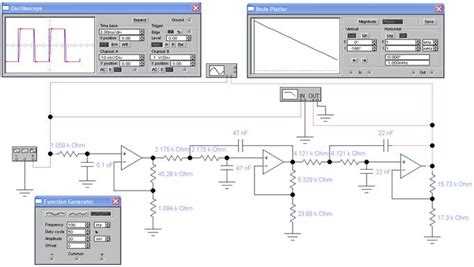
Для анализа амплитудно-частотной и фазо-частотной характеристик в Mathcad необходимо предварительно импортировать экспериментальные данные в виде частотно-зависимых значений. Оптимальный формат исходных файлов – CSV или TXT с разделителями (запятая, табуляция, точка с запятой). В каждой строке должны содержаться значения частоты, амплитуды и фазы (в градусах или радианах).
В Mathcad используйте функцию READCSV("путь_к_файлу") или READPRN("путь_к_файлу") для загрузки данных. Присвойте результат переменной, например data := READCSV("data.csv"). Убедитесь, что данные загружаются в виде матрицы, где каждая строка соответствует одной точке измерений. Выделите столбцы: f := data[0..n-1, 0] – частота, A := data[0..n-1, 1] – амплитуда, φ := data[0..n-1, 2] – фаза.
Перед построением графиков преобразуйте амплитуду в децибелы: A_dB := 20 * log10(A). Если фаза задана в градусах, при необходимости переведите её в радианы: φ_rad := φ * π / 180. Для построения АЧХ используйте функцию plot(f, A_dB), для ФЧХ – plot(f, φ_rad).
Убедитесь, что частоты отсортированы по возрастанию. При наличии шумов или пропущенных значений предварительно отфильтруйте данные или используйте интерполяцию с функцией interp. Для проверки целостности данных используйте команды rows(data) и cols(data) для диагностики размеров матрицы.
Определение амплитудной и фазовой характеристик на основе уравнений системы
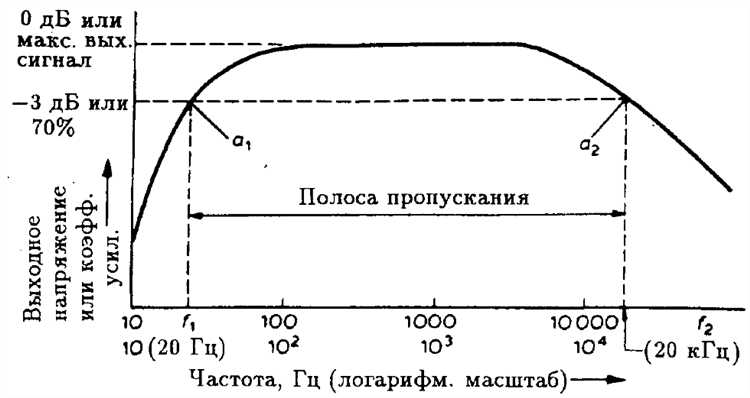
Для вычисления амплитудной и фазовой частотных характеристик (АЧХ и ФЧХ) в Mathcad необходимо исходить из дифференциального уравнения, описывающего линейную систему. Например, пусть задано уравнение второго порядка:
a₂·y»(t) + a₁·y'(t) + a₀·y(t) = b₁·x'(t) + b₀·x(t)
Переход к частотной области осуществляется через преобразование Фурье или Лапласа. В Mathcad удобно использовать операторную форму замены производных: d/dt → jω. После подстановки получаем передаточную функцию:
H(jω) = Y(jω) / X(jω) = (b₁·jω + b₀) / (a₂·(jω)² + a₁·jω + a₀)
Для построения АЧХ в Mathcad следует задать диапазон частот ω, вычислить модуль передаточной функции с помощью функции abs(H(jω)). ФЧХ строится через аргумент комплексной функции: arg(H(jω)), возвращающий фазовый сдвиг в радианах. При необходимости, фаза переводится в градусы умножением на 180/π.
Рекомендуется использовать частотный вектор с логарифмическим шагом для повышения информативности графиков: ω := 10^x, x ∈ [xmin, xmax]. Это позволяет визуализировать поведение системы в широком диапазоне частот без потери точности.
После вычисления значений abs(H(jω)) и arg(H(jω)), используйте встроенные функции plot для построения графиков. При работе с комплексными выражениями обязательно указывайте j := √–1 в начале документа, чтобы избежать ошибок интерпретации.
Преобразование передаточной функции в частотную область в Mathcad
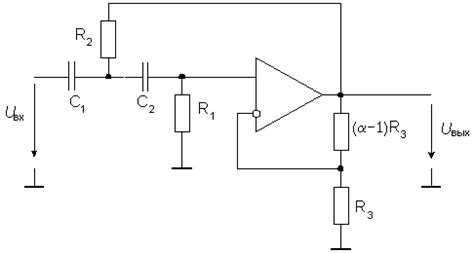
Для анализа частотных характеристик системы в Mathcad необходимо представить передаточную функцию в виде зависимости от комплексной частоты \( s = j\omega \). Передаточная функция \( H(s) \) вводится в символьной форме с использованием переменной \( s \), например: H(s) := (s + 2) / (s^2 + 3s + 2).
Замену переменной \( s \) на \( j\omega \) выполняют с помощью подстановки: H(j*ω) := substitute(H(s), s, j*ω). Это преобразование позволяет получить выражение, зависящее только от частоты \( \omega \), где j := √-1 задается явно, если Mathcad этого требует.
Для построения АЧХ и ФЧХ необходимо определить диапазон частот. Создается вектор частот: ω := linspace(0.1, 100, 1000). Затем вычисляется частотная характеристика: Hf := eval(H(j*ω)).
Амплитудно-частотная характеристика получается как модуль комплексной функции: A(ω) := abs(Hf). Фазовая – как аргумент: Φ(ω) := arg(Hf). Для удобства интерпретации АЧХ часто отображается в децибелах: A_dB(ω) := 20 * log10(A(ω)).
Графики строятся с использованием стандартных средств Mathcad. Команды: plot(ω, A_dB(ω)) для АЧХ и plot(ω, Φ(ω)) для ФЧХ. Обязательно задавать единицы измерения, если используются физические частоты (например, рад/с).
Если передаточная функция задана через коэффициенты числителя и знаменателя, используют встроенную функцию transfer совместно с FourierTransform или численным методом с преобразованием Лапласа и последующей заменой \( s \) на \( j\omega \).
В случае резонансных систем особое внимание уделяется разрешающей способности частотного вектора – недостаточное количество точек вблизи резонансной частоты искажает графики. Увеличение плотности точек в критических диапазонах достигается через ручное задание частотной сетки.
Использование встроенных функций Mathcad для расчёта АЧХ и ФЧХ
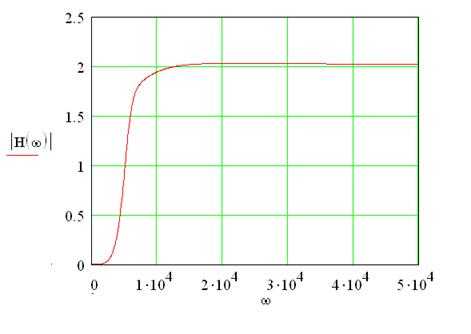
Для анализа частотных характеристик систем в Mathcad применяются функции обработки сигналов и комплексного анализа. Наиболее эффективно использовать встроенные функции fft, arg и abs.
- Функция
fft– быстрое преобразование Фурье. Применяется к сигналу или импульсной характеристике, представленной в виде вектора. Результат – спектр в комплексной форме. Для корректной интерпретации необходимо учесть дискретизацию: частотная ось рассчитывается по формулеf := (0..N-1) * (fs / N), гдеN– длина сигнала,fs– частота дискретизации. - Функция
absизвлекает амплитудную характеристику (АЧХ) из спектра. Применяется к результатуfft:A(f) := abs(fft(h)), гдеh– импульсная характеристика системы.
- Функция
argвозвращает фазовый спектр, необходимый для построения ФЧХ. Используется аналогично:φ(f) := arg(fft(h)).
Для систем, описанных передаточной функцией в виде дробно-рационального выражения, можно использовать функцию polyroots для поиска нулей и полюсов, а затем численно рассчитать частотный отклик:
- Задать числитель и знаменатель передаточной функции как векторы коэффициентов.
- Для каждого значения частоты
ωвычислить комплексную частотуs := j·ωи подставить в выражение H(s). - Построить графики модуля и аргумента
H(jω).
Рекомендуется использовать логарифмическую шкалу при построении АЧХ и ФЧХ: 20·log10(abs(H(jω))) для амплитудной и unwrap(arg(H(jω))) для фазовой характеристики. Для этого Mathcad позволяет применять функции log и пользовательскую фазовую развёртку.
Настройка диапазона частот и логарифмического масштаба при построении графиков
Для точного анализа амплитудно-частотной характеристики (АЧХ) и фазочастотной характеристики (ФЧХ) в Mathcad необходимо правильно задать диапазон частот. Рекомендуется выбирать частотный интервал с учётом особенностей исследуемой системы: нижняя граница – минимум на порядок ниже минимальной частоты интересующего сигнала, верхняя – на порядок выше максимальной. Это обеспечивает покрытие всех значимых точек изменения характеристик.
Логарифмический масштаб по оси частот позволяет наглядно визуализировать изменения в широком диапазоне, особенно при исследовании фильтров и систем с экспоненциальным поведением. В Mathcad для построения графиков с логарифмическим масштабом следует предварительно выполнить преобразование частот: применить логарифм по основанию 10 к массиву частот, а затем построить график по преобразованным данным. Настройка оси производится вручную через параметры графика, где задаются подписи, соответствующие исходным значениям частот, для сохранения информативности.
При работе с логарифмическим масштабом важно выбирать равномерные точки по логарифму частоты, а не по линейной шкале, чтобы избежать концентрации данных в узком участке. Использование функции logspace для генерации частотного вектора обеспечивает равномерное распределение точек в логарифмическом масштабе и повышает точность построения АЧХ и ФЧХ.
Сравнение теоретических и экспериментальных АЧХ и ФЧХ на одном графике
Для корректного сопоставления теоретической и экспериментальной амплитудно-частотной характеристики (АЧХ) и фазочастотной характеристики (ФЧХ) в Mathcad необходимо использовать единый масштаб осей и идентичный набор частотных точек. Это исключит искажения, связанные с интерполяцией данных и разной дискретностью измерений.
Рекомендуется строить графики АЧХ и ФЧХ на одной координатной плоскости, используя два разных цвета для теории и эксперимента. Важна настройка прозрачности линий для визуального выявления зон совпадения и расхождения. В Mathcad применяйте функцию plot с параметром overlay.
Для оценки соответствия результатов применяют вычисление отклонений амплитуд и фаз на каждой частоте: ΔA = |A_теор — A_эксп|, ΔΦ = |Φ_теор — Φ_эксп|. Практически целесообразно выделять диапазоны частот с максимальными расхождениями и анализировать причины – например, влияние шумов, нелинейностей или неточностей модели.
Оптимальная частотная сетка должна покрывать минимум 50 точек с равномерным распределением по логарифмической шкале, что повышает информативность графика и точность сравнений.
Использование совместного графика облегчает выявление критических частот, где фаза смещается на 90° или амплитуда падает на 3 дБ, и позволяет быстро проверить адекватность теоретической модели.
Вопрос-ответ:
Как в Mathcad построить амплитудно-частотную характеристику (АЧХ) сигнала?
Для построения АЧХ в Mathcad необходимо задать функцию передачи или сигнал, для которого проводится анализ. Затем с помощью встроенных инструментов вычисляется модуль комплексной функции зависимости от частоты. Обычно сначала формируется массив значений частоты, а потом для каждой частоты вычисляется значение функции передачи. Результаты визуализируются с помощью графика, где по оси X откладывается частота, а по оси Y — амплитуда. Такой подход позволяет увидеть, как изменяется усиление или затухание сигнала на разных частотах.
Что необходимо учитывать при построении фазочастотной характеристики (ФЧХ) в Mathcad?
При построении ФЧХ важно корректно вычислить фазовый угол комплексной функции передачи. В Mathcad для этого применяется функция аргумента комплексного числа. Следует учитывать, что фаза может принимать значения от -π до π, поэтому для анализа часто используется развёртка фазы, чтобы избежать скачков и сделать график более понятным. Кроме того, для получения точных результатов нужно правильно определить диапазон частот и достаточную плотность точек, чтобы выявить особенности изменения фазы.
Как можно автоматизировать построение АЧХ и ФЧХ для различных параметров системы в Mathcad?
В Mathcad можно создавать параметры системы в виде переменных, а затем использовать циклы или массивы для перебора значений этих параметров. Например, если нужно исследовать влияние изменения сопротивления или емкости на АЧХ и ФЧХ, можно задать соответствующие диапазоны и в цикле вычислять характеристики для каждого набора значений. Результаты можно вывести в виде серии графиков или наложить на один, чтобы сравнить изменения. Такой подход позволяет быстро анализировать влияние параметров без необходимости каждый раз вручную менять формулы.
Какие функции Mathcad удобны для работы с комплексными числами при анализе частотных характеристик?
Mathcad содержит множество функций для комплексных чисел, которые помогают при анализе АЧХ и ФЧХ. Для получения модуля используется функция abs(), для вычисления фазы — arg(). Чтобы работать с комплексными выражениями, удобно использовать встроенную поддержку комплексных переменных и операций. Также доступны функции для преобразований и представления чисел в алгебраической или тригонометрической форме, что упрощает анализ и визуализацию результатов.
Какие ошибки часто возникают при построении АЧХ и ФЧХ в Mathcad и как их избежать?
Одной из распространённых ошибок является неправильный выбор диапазона частот — слишком узкий или слишком широкий, что приводит к недостаточной детализации графика или избыточным вычислениям. Также часто встречается неверный расчет фазы без развёртки, из-за чего график получается с резкими скачками. Ошибки могут возникать при использовании функций комплексных чисел, например, если забыть перевести углы в радианы, если требуется. Чтобы избежать проблем, рекомендуется внимательно проверять исходные данные, использовать адекватный шаг по частоте и проверять корректность функций, применяемых для вычислений.