Как построить афчх в maple

Программный комплекс Maple предоставляет точные и наглядные средства для анализа частотных характеристик линейных систем. Построение амплитудно-фазовой характеристики (АФХ) в Maple осуществляется с помощью функций из пакета DynamicSystems или посредством символьных и численных преобразований. Основным преимуществом Maple является возможность комбинирования аналитических решений с интерактивной визуализацией, что особенно важно при работе с передаточными функциями высокой сложности.

Для начала необходимо определить передаточную функцию в виде дробно-рационального выражения от переменной s или jω. Например, H(s) = (2s + 5)/(s² + 3s + 2). Используя функцию freqresp из пакета DynamicSystems, можно получить вектор значений модуля и фазы в заданном диапазоне частот. Рекомендуется использовать логарифмическую шкалу по оси частот, что позволяет более точно анализировать поведение системы в широком диапазоне.

Для построения графика используется команда polarplot или plot с параметрами abs и argument, применяемыми к частотному отклику. Важно задать достаточную плотность точек на частотной оси, чтобы избежать искажения формы АФХ. Например, интервал частот от 0.1 до 100 рад/с следует дискретизировать не менее чем на 500 точек. Это обеспечит гладкое и точное отображение амплитудной и фазовой составляющих.

Maple позволяет также выполнять символьное разложение частотного отклика, что полезно при теоретическом анализе систем. Выражения для амплитуды и фазы могут быть упрощены с помощью команды simplify, что особенно актуально при анализе устойчивости или разработке фильтров. Использование Maple для построения АФХ обеспечивает не только визуальное представление, но и глубокое аналитическое понимание поведения системы в частотной области.

Задание передаточной функции через символьные выражения

В Maple передаточная функция системы может быть задана с использованием пакета DynamicSystems или вручную через символьные выражения. Для ручного задания необходимо определить числитель и знаменатель в виде полиномов от переменной s или jω, используя функции пакета Student[Calculus1] или стандартные средства символьной алгебры.

Пример задания передаточной функции вручную:


with(Student[Calculus1]):
restart:
s := 's':
G := (10*s^2 + 5*s + 1)/(s^3 + 4*s^2 + 6*s + 2);


Функция G в данном случае – это рациональная функция от комплексной переменной s. Она используется в дальнейшем для анализа устойчивости, построения амплитудно-фазовых характеристик и моделирования.

Для упрощения выражений применяйте функцию simplify(). При необходимости разложения на элементарные дроби – convert(G, parfrac). Для последующей работы с частотными характеристиками переходите к подстановке s = I*ω с помощью команды subs(s=I*ω, G).

Использование символьных выражений позволяет точно контролировать структуру передаточной функции, избежать численных ошибок и получить аналитические зависимости, пригодные для дифференцирования, интегрирования и предельного анализа.

Преобразование передаточной функции к частотной форме

Передаточная функция \( W(s) \) в области Лапласа должна быть приведена к форме \( W(j\omega) \) для анализа амплитудно-фазовой характеристики. В Maple это достигается подстановкой \( s = j\omega \), где \( j \) – мнимая единица, а \( \omega \) – круговая частота. Используйте команду subs(s = I*omega, W) для выполнения этой подстановки.

Для корректного преобразования рациональной функции рекомендуется предварительно упростить её с помощью simplify и expand, чтобы избежать ошибочного анализа скрытых сингулярностей. Если числитель и знаменатель содержат параметры, используйте assume для задания допустимого диапазона значений, особенно если требуется построение графика при конкретных условиях.

Команда evalf в Maple применяется для получения численного представления выражений, содержащих символические переменные. При построении амплитудно-фазовой характеристики (АФХ) эта команда необходима для перехода от аналитической формы к числовым значениям, пригодным для графической визуализации.

• Для численного анализа частотных характеристик комплексного выражения вида H(ω) = subs(s = I*ω, H(s)) используется evalf при подстановке значений частоты ω.
• При построении списков значений для графика необходимо использовать evalf в цикле или при векторизации: map(evalf, [seq(H(ω), ω = 0..100)]).
• Для повышения точности допустимо использовать аргумент digits: evalf(expr, 20) – вычисление с 20 значащими цифрами.
• Если выражение содержит параметры, не подлежащие численному анализу, необходимо предварительно выполнить subs для всех символических величин перед вызовом evalf.

Без применения evalf Maple не сможет построить корректные графики АФХ, так как функция plot требует числовых значений. Поэтому evalf должна использоваться систематически на всех этапах численного построения характеристик.

Создание массива частот и вычисление комплексного отклика

Для построения амплитудно-фазовой характеристики необходимо сформировать массив частот и вычислить комплексный отклик системы на каждой из них. В Maple массив частот удобно задавать с помощью команды Array или Vector из пакета LinearAlgebra. Например, для логарифмически распределённых значений от 1 Гц до 10 кГц используется:

omega := [seq(2*Pi*10^x, x = 0..4, 0.1)]:

Это создаёт массив частот в радианах в логарифмическом масштабе. Для вычисления отклика необходимо задать передаточную функцию в виде дробно-рационального выражения. Например:

H := (s) -> (s + 10)/(s^2 + 2*s + 100):

Далее проводится подстановка комплексной переменной s = I*ω для каждого значения из массива:

H_vals := [seq(H(I*ωi), ωi in omega)]:

В результате H_vals содержит комплексные значения отклика, соответствующие каждой частоте. Эти значения далее используются для расчёта амплитуд и фаз. Для амплитуды применяется abs, для фазы – argument:

amplitudes := [seq(abs(H(I*ωi)), ωi in omega)]:

phases := [seq(argument(H(I*ωi)), ωi in omega)]:

Рекомендуется сохранять массивы omega, amplitudes и phases для последующего построения графиков в логарифмических координатах. Это обеспечивает точное отображение поведения системы в широком диапазоне частот.

Построение амплитудной характеристики с помощью plot

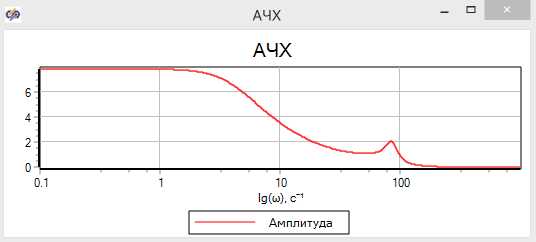
Для построения амплитудной характеристики в Maple необходимо задать передаточную функцию в частотной области. Пример:

H := (s) -> (10)/(s^2 + 2*s + 10);

Замените s на мнимую единицу, умноженную на частоту: omega := 0..50; и Hj := (omega) -> evalf(abs(H(I*omega)));

Функция abs извлекает амплитуду (модуль) комплексной функции. Команда для построения графика:

plot(Hj(omega), omega = 0..50, labels = ["ω", "|H(jω)|"], title = "Амплитудная характеристика");

Убедитесь, что функция определена на допустимом частотном диапазоне. Используйте evalf для обеспечения численного результата. В случае логарифмической шкалы используйте logplot из пакета plots:

with(plots): logplot(Hj(omega), omega = 0.1..100, labels = ["ω", "|H(jω)|"], title = "Амплитудная характеристика (логарифмическая шкала)");

Для корректного отображения в широком диапазоне частот желательно избегать нуля в нижней границе диапазона. Используйте положительные значения, например от 0.1. Все вычисления выполняйте в числовой форме во избежание потерь точности при работе с комплексными выражениями.

Отображение фазовой характеристики на том же графике

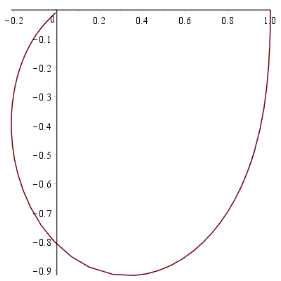
Для отображения фазовой характеристики совместно с амплитудной в Maple удобно использовать двойную систему координат с привязкой к одному графику. Основной инструмент – процедура plots[display] с опцией axes=boxed и наложением графиков через список.

Рассчитайте амплитуду и фазу функции передаточной характеристики H(ω), используя модуль и аргумент комплексного выражения:

A(ω) := abs(H(ω));

φ(ω) := argument(H(ω));

Постройте амплитудную характеристику с одной шкалой осей:

plot1 := plot(A(ω), ω=ωmin..ωmax, color=blue, legend=»Амплитуда»);

Для фазовой характеристики определите масштаб второй оси, если фазовые значения выходят за пределы амплитудных. Используйте plots[twoaxisplot]:

with(plots):

plot2 := twoaxisplot([A(ω), φ(ω)], ω=ωmin..ωmax, color=[blue, red], legend=[«Амплитуда», «Фаза»]);

Фаза будет отображена справа, с отдельной вертикальной шкалой. Следите, чтобы значения фазы были приведены к диапазону (−π, π] или [0, 2π), в зависимости от требований анализа. Для этого используйте:

φ(ω) := simplify(argument(H(ω)), symbolic);

В случае логарифмической шкалы по оси частот замените plot на semilogplot или примените логарифмическое преобразование вручную перед построением:

ωlog := log[10](ω);

Итоговая визуализация: display(plot2); – объединяет амплитуду и фазу на одном графике с читаемым разделением осей и легендой. Это обеспечивает наглядность анализа частотных характеристик.

Вопрос-ответ:

Можно ли построить амплитудно-фазовую характеристику для передаточной функции в Maple без использования сторонних пакетов?

Да, Maple предоставляет встроенные средства для работы с передаточными функциями и построения графиков. Например, можно использовать стандартные функции из пакета `DynamicSystems` для задания передаточной функции и получения амплитудно-фазовой характеристики. Дополнительные пакеты могут упростить некоторые шаги, но для базовых задач достаточно встроенных инструментов.

Можно ли в Maple построить амплитудно-фазовую характеристику по экспериментальным данным, а не по теоретической модели?

Да, можно. Если у вас есть набор экспериментальных данных в виде амплитуд и фаз на определённых частотах, их можно представить в виде таблицы или массива и использовать функции построения графиков, такие как `plot` или `polarplot`. Однако это уже не будет автоматическое построение по передаточной функции, а ручное отображение данных. Для анализа и сравнения можно также наложить эти данные на теоретическую характеристику.

Какие трудности могут возникнуть при построении амплитудно-фазовой характеристики в Maple?

Часто возникают трудности с правильным определением комплексной переменной и диапазона частот. Например, если использовать частоту в герцах, нужно преобразовать её в радианы в секунду. Ещё одна распространённая ошибка — неправильное использование логарифмической шкалы. Maple требует явного указания масштаба осей. Также стоит внимательно следить за единицами измерения и синтаксисом — любые неточности могут привести к некорректному графику или ошибке выполнения.

Как построить амплитудно-фазовую характеристику в виде одного графика в полярных координатах?

В Maple можно использовать функцию `polarplot`, указав в качестве радиуса амплитуду, а в качестве угла — фазу сигнала. Например, если вы вычислили значение передаточной функции на диапазоне частот, то можно создать список комплексных значений, затем извлечь модуль и аргумент и построить график в полярных координатах. Это потребует ручной обработки данных, но позволяет наглядно представить зависимость амплитуды и фазы.