Как транспонировать матрицу в wolfram mathematica

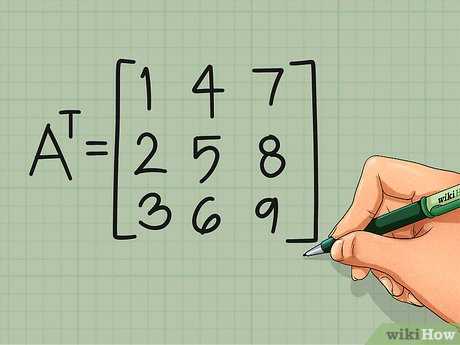
В Wolfram Mathematica для транспонирования матрицы используется встроенная функция Transpose. Это базовая операция линейной алгебры, которая меняет строки матрицы на столбцы и наоборот. Транспонированная матрица сохраняет все элементы исходной, но изменяет их расположение в соответствии с новой структурой.

Для того чтобы транспонировать матрицу, достаточно передать её в качестве аргумента функции. Пример: Transpose[{{1, 2, 3}, {4, 5, 6}}] вернёт результат {{1, 4}, {2, 5}, {3, 6}}. Это стандартный способ работы с матрицами, но Mathematica также поддерживает более сложные операции с многомерными массивами, используя соответствующие методы и опции.

Важно: если вам нужно транспонировать матрицу внутри более сложных выражений или в контексте численных вычислений, функции Mathematica позволяют интегрировать эту операцию в состав более крупных программных конструкций, что ускоряет работу с большими данными.

Для работы с матрицами размером 1xN или Nx1 транспонирование меняет форму векторных объектов. Например, вектор {1, 2, 3} после транспонирования станет {{1}, {2}, {3}}. Важно помнить, что операцию транспонирования можно применить не только к двумерным матрицам, но и к более сложным структурам данных, включая многомерные массивы.

Математические операции с транспонированными матрицами в Wolfram Mathematica, такие как умножение, также можно выполнить с использованием стандартных операторов и функций, обеспечивая высокую гибкость при решении задач линейной алгебры.

Основные способы транспонирования в Mathematica

В Mathematica существует несколько способов транспонирования матрицы, каждый из которых может быть полезен в зависимости от контекста задачи. Вот основные методы:

• Функция Transpose – это базовый способ транспонирования матрицы. Он меняет строки на столбцы и наоборот. Пример:

Transpose[{{1, 2, 3}, {4, 5, 6}}]

• Функция MatrixTranspose – работает аналогично Transpose, но является более специализированным вариантом, используемым в основном для матриц. Пример:

MatrixTranspose[{{1, 2}, {3, 4}}]

• Использование @Transpose в комбинации с операторами – если нужно транспонировать только часть выражения, можно использовать комбинированный оператор с транспонированием. Пример:

f[x_] := {x, x^2};
f[Transpose[{1, 2, 3}]]

• Транспонирование с учетом вложенных структур – если матрица содержит вложенные списки, транспонирование происходит по всем уровням вложенности. Это полезно для многомерных массивов. Пример:

Transpose[{{1, {2, 3}}, {4, {5, 6}}}]

• Транспонирование разреженных матриц – для разреженных матриц, когда важна производительность, можно использовать специализированную функцию SparseArray, чтобы транспонировать матрицы с минимальными затратами по памяти. Пример:

SparseArray[{{1, 2} -> 1, {2, 1} -> 2}];
SparseArray[Transpose[{{1, 2}, {3, 4}}]]

• Перестановка индексов с Transpose[{i, j}] – в некоторых случаях необходимо транспонировать матрицу с учетом определенной перестановки индексов. Это позволяет изменить порядок столбцов и строк согласно заданным индексам. Пример:

Transpose[{{1, 2, 3}, {4, 5, 6}}, {2, 1}]

В зависимости от сложности задачи и особенностей матрицы, можно выбрать наиболее подходящий способ транспонирования. Все методы работают эффективно в Mathematica и могут быть применены в различных контекстах вычислений.

Использование функции Transpose для матриц

В Wolfram Mathematica функция Transpose используется для транспонирования матриц, то есть для замены строк и столбцов местами. Это полезно при работе с многомерными массивами данных и решении различных математических задач.

Синтаксис функции: Transpose[matrix], где matrix – это объект, который поддается транспонированию (двумерная матрица, список списков и т.д.). Функция возвращает новую матрицу, в которой строки исходной матрицы становятся столбцами и наоборот.

Пример: допустим, у нас есть матрица m = {{1, 2, 3}, {4, 5, 6}}. Применение Transpose[m] приведет к результату {{1, 4}, {2, 5}, {3, 6}}.

Если транспонировать матрицу несколько раз, то результат вернется к исходному виду. Например, для матрицы m = {{1, 2}, {3, 4}}, двойное транспонирование: Transpose[Transpose[m]] даст {{1, 2}, {3, 4}}.

Для многомерных массивов можно использовать функцию Transpose с дополнительными аргументами. Например, Transpose[matrix, {2, 1, 3}] изменит порядок индексов в многомерном массиве. Это полезно для изменения структуры данных в задачах обработки тензоров.

Следует помнить, что транспонирование не изменяет саму матрицу, а возвращает новую структуру. Для сохранения результата можно присвоить его новой переменной.

Транспонирование разреженных матриц

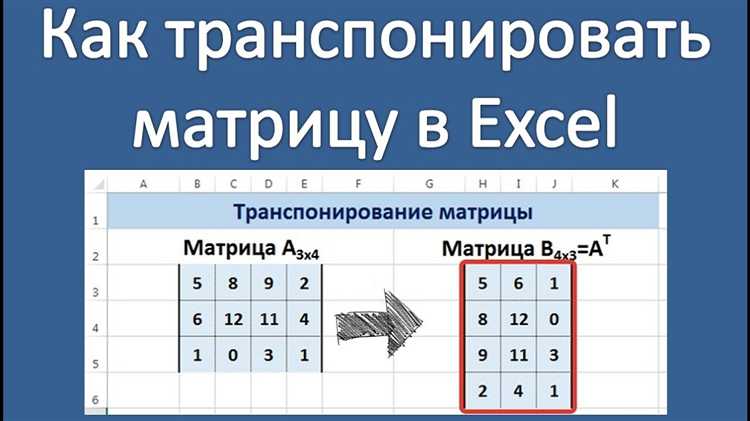
В Wolfram Mathematica для работы с разреженными матрицами используется специальный тип данных SparseArray. Это позволяет эффективно хранить и обрабатывать матрицы, содержащие большое количество нулевых элементов. Транспонирование таких матриц выполняется с использованием стандартной функции Transpose, которая сохраняет структуру разреженности, обеспечивая минимизацию использования памяти и улучшение производительности.

При транспонировании разреженной матрицы важно, что Wolfram Mathematica не создаёт полный набор элементов для матрицы, а работает только с ненулевыми значениями. Таким образом, результатом применения функции Transpose к объекту типа SparseArray будет также разреженная матрица, содержащая те же ненулевые элементы, но расположенные на новых индексах, соответствующих транспонированной структуре.

Пример транспонирования разреженной матрицы в Mathematica:

A = SparseArray[{(1, 2) -> 5, (3, 4) -> 8, (2, 3) -> 6}];
Transpose[A]

В данном примере создается разреженная матрица с ненулевыми значениями в элементах (1,2), (3,4) и (2,3). Транспонированная матрица будет содержать элементы в позициях (2,1), (4,3) и (3,2), сохраняя разреженность.

Транспонирование разреженных матриц в Mathematica осуществляется без изменений самой структуры хранения данных. Это означает, что операции над разреженными матрицами остаются быстрыми, даже если сам результат транспонирования занимает намного больше памяти при использовании стандартных матриц.

Если необходимо ускорить выполнение операций над разреженными матрицами, рекомендуется избегать их явного преобразования в полные матрицы, а использовать встроенные методы для обработки разреженных данных в контексте операций с матрицами.

Как транспонировать только определённые строки или столбцы

В Wolfram Mathematica транспонировать только определённые строки или столбцы матрицы можно с помощью нескольких методов. Для этого следует использовать функции и манипуляции, которые позволяют изолировать нужные элементы и транспонировать их, не затрагивая остальные.

Одним из самых простых способов является использование индексации для выбора нужных строк или столбцов, после чего применяется функция Transpose только к этим частям матрицы.

Транспонирование строк

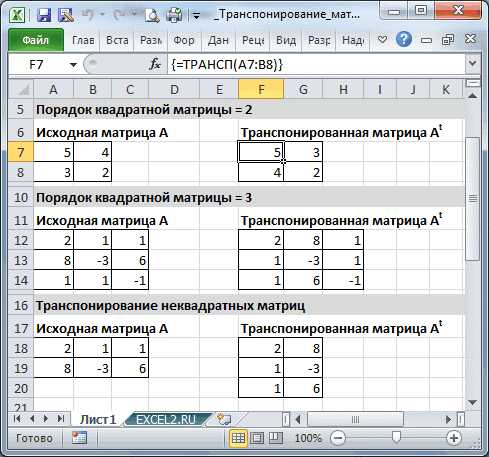
Если необходимо транспонировать только определённые строки матрицы, сначала выберите их через индексирование, а затем примените Transpose. Например, чтобы транспонировать первую и третью строки матрицы m, можно использовать следующий код:

Transpose[m[[{1, 3}, All]]]

Здесь m[[{1, 3}, All]] извлекает первую и третью строки матрицы, а Transpose меняет их местами.

Транспонирование столбцов

Для транспонирования определённых столбцов аналогично выбираем их с помощью индексации:

Transpose[m[[All, {2, 4}]]]

Этот код транспонирует второй и четвёртый столбцы матрицы m, оставляя остальные неизменными.

Транспонирование как отдельная операция

Если нужно транспонировать только отдельные элементы строки или столбца, можно комбинировать их с другими операциями, например, с Part для точечной выборки. Пример для транспонирования первого столбца:

Transpose[{m[[All, 1]]}]

Это создаст транспонированную версию первого столбца, а остальные столбцы останутся без изменений.

Использование функции Map

В Wolfram Mathematica транспонирование многомерных массивов (тензоров) осуществляется с помощью функции Transpose. Для двумерных матриц этот процесс интуитивно понятен: строки заменяются на столбцы. Однако для многомерных массивов нужно учитывать порядок измерений, что может быть менее очевидно.

Для многомерного массива A с размерами m × n × p вызов Transpose[A] по умолчанию выполнит перестановку первых двух осей. То есть если у вас массив размером 2×3×4, то результат транспонирования будет иметь размер 3×2×4. Однако порядок осей можно изменять, указывая аргумент функции в виде списка индексов.

Например, для массива размером 2 × 3 × 4, чтобы поменять местами вторую и третью оси, можно вызвать:

Transpose[A, {1, 3, 2}]

Это приведет к изменению порядка осей, и результирующий массив будет иметь размеры 2 × 4 × 3.

Также возможно транспонировать части массива, используя функцию Transpose в сочетании с функциями Take и Drop. Например, если нужно транспонировать только одну из плоскостей многомерного массива, можно выделить эту плоскость и применить к ней транспонирование.

Для работы с многомерными массивами важно помнить, что они могут быть как тензорами с несколькими измерениями, так и более сложными структурами данных. В таких случаях Transpose помогает быстро адаптировать данные под нужный формат, не прибегая к дополнительным вычислениям.

При работе с большими массивами транспонирование может оказаться ресурсоемким процессом. Важно учитывать, что многократные операции могут сильно замедлить вычисления, особенно при работе с массивами большого размера. Поэтому рекомендуется заранее планировать структуру данных и минимизировать количество транспонирующих операций.

Оптимизация транспонирования больших матриц

В Wolfram Mathematica транспонирование больших матриц может стать ресурсозатратным процессом, особенно при работе с матрицами размером от десятков тысяч до миллионов элементов. Чтобы ускорить этот процесс, можно применить несколько методов оптимизации.

1. Использование встроенных функций для работы с матрицами

Mathematica обладает встроенными оптимизациями для стандартных операций. Использование функции Transpose в большинстве случаев даёт наилучший результат, так как она оптимизирована для быстродействия. Однако для очень больших матриц её производительность может быть ограничена, особенно при недостатке памяти.

2. Использование памяти с умом

Перемещение данных в память и управление ею имеют критическое значение при транспонировании больших матриц. Для минимизации расхода памяти стоит использовать встроенные возможности Mathematica для работы с большими данными, например, SparseArray. Это позволит значительно снизить объём занимаемой памяти при работе с разреженными матрицами, где большинство элементов равны нулю.

3. Параллельная обработка

Для ускорения транспонирования можно воспользоваться параллельными вычислениями. Mathematica поддерживает параллельное выполнение через Parallelize, что может быть полезно для распределения нагрузки на несколько ядер процессора. Например, транспонирование больших матриц можно разбить на несколько частей, каждую из которых будет обрабатывать отдельный процессор.

4. Использование специализированных алгоритмов

Для некоторых типов матриц, например, блочных или диагональных, можно разработать более быстрые алгоритмы транспонирования. В таких случаях важно понимать структуру матрицы и использовать алгоритмы, которые минимизируют необходимость в перестановке данных в памяти. Например, можно использовать алгоритм блочного транспонирования для работы с матрицами, разделёнными на подматрицы.

5. Сохранение промежуточных результатов

При многократном транспонировании одних и тех же матриц можно сохранить промежуточные результаты, чтобы избежать повторных вычислений. Например, если задача требует транспонирования нескольких матриц в одной и той же программе, имеет смысл заранее сохранить результаты транспонирования, чтобы в дальнейшем избежать повторных операций.

6. Использование внешних библиотек

Если стандартных средств Mathematica недостаточно, можно обратиться к внешним библиотекам для работы с большими матрицами. Библиотеки на C или Fortran, такие как BLAS или LAPACK, могут быть интегрированы с Mathematica для более эффективного выполнения операций с матрицами.

Ошибки при транспонировании и как их избежать

Основная ошибка при транспонировании матриц в Wolfram Mathematica – неправильное использование оператора транспонирования. В языке Wolfram Mathematica для транспонирования матрицы следует использовать функцию Transpose, а не оператор «перевернутой» скобки ', который работает в некоторых других математических программных средах.

Ещё одна распространенная ошибка – это неправильное представление матрицы. В Mathematica матрица задается как список списков. Например, для матрицы 2×3 нужно использовать конструкцию {{1, 2, 3}, {4, 5, 6}}, где каждый внутренний список представляет строку матрицы. Если один из элементов не является списком, результат транспонирования может быть непредсказуемым.

Также стоит быть внимательным при работе с матрицами разного размера. Например, транспонирование матрицы 1xN превратит её в матрицу Nx1. Не стоит ожидать, что операции, рассчитанные на квадратные матрицы, будут корректно работать с прямоугольными.

При работе с матрицами с элементами различных типов данных (например, числа и строки) также может возникнуть ошибка. Mathematica не всегда сможет корректно транспонировать такие структуры, если элементы содержат разнородные типы данных. Важно следить за единообразием типов данных в элементах матрицы.

Чтобы избежать ошибок при транспонировании, полезно перед выполнением операции проверять размерность матрицы с помощью Dimensions. Это позволит убедиться, что операцию можно провести без ошибок и неожиданного изменения структуры данных.

Вопрос-ответ:

Как транспонировать матрицу в Wolfram Mathematica?

В Wolfram Mathematica транспонировать матрицу можно с помощью функции `Transpose`. Например, если у вас есть матрица `A`, то для ее транспонирования нужно просто написать: `Transpose[A]`. Это действие заменяет строки на столбцы и наоборот.

Можно ли транспонировать матрицу только по одному измерению в Mathematica?

Да, можно. В Mathematica можно использовать функцию `Transpose` с дополнительным аргументом, чтобы транспонировать только определенные оси матрицы. Например, для транспонирования только строк или столбцов, можно указать аргументы, которые соответствуют нужным измерениям. Например: `Transpose[A, {2, 1}]` — это транспонирование по первому и второму измерению, меняя местами строки и столбцы.

Что делать, если в матрице есть строки разной длины?

Если матрица имеет строки разной длины, то в Mathematica она будет рассматриваться как список списков. При попытке транспонировать такую «матрицу» с помощью функции `Transpose`, вы получите ошибку. Чтобы избежать этого, можно сначала привести данные к правильному виду или использовать функцию `PadRight`, которая дополняет строки до одинаковой длины.

Как транспонировать матрицу и сохранить её как новый объект в Mathematica?

Чтобы сохранить транспонированную матрицу как новый объект в Mathematica, нужно просто присвоить результат транспонирования новой переменной. Например, если у вас есть матрица `A`, и вы хотите создать её транспонированную версию в переменной `B`, вы можете сделать так: `B = Transpose[A]`. Теперь `B` будет содержать транспонированную матрицу.

Какие особенности имеет транспонирование тензоров в Mathematica?

Транспонирование тензоров в Mathematica работает аналогично транспонированию матриц, но с дополнительными параметрами для более высоких размерностей. В функции `Transpose` можно указать порядок осей, которые вы хотите поменять местами. Например, для тензора с тремя измерениями, вызов `Transpose[Tensor, {3, 2, 1}]` поменяет местами оси в тензоре. Если оси не указаны, они будут транспонированы в стандартном порядке, меняя местами все измерения.