Mathcad предоставляет мощные средства для визуализации данных в трех измерениях, позволяя точно анализировать поведение функций, поверхностей и объемных распределений. При работе с трехмерными графиками в Mathcad доступны различные типы отображения, включая Surface Plot, Contour Plot и 3D Bar Plot. Каждый из них решает специфические задачи моделирования и интерпретации данных.
Surface Plot используется для отображения непрерывной поверхности, заданной функцией двух переменных. Этот тип графика особенно полезен для анализа поведения математических моделей, например, при визуализации тепловых полей или функций плотности вероятности. При настройке графика рекомендуется вручную задавать диапазоны переменных и шаг дискретизации для повышения точности отображения.
Contour Plot позволяет отобразить изолинии высот на плоскости XY, что удобно при анализе градиентов и поиска экстремумов. В Mathcad этот график может быть наложен на поверхность, что позволяет одновременно оценивать форму и уровни значения функции. Эффективное использование цветовых шкал существенно упрощает интерпретацию таких графиков.
3D Bar Plot применяется реже, но он полезен при сравнении дискретных наборов данных в трехмерной системе координат. Например, его удобно использовать для представления объемов продаж по регионам и кварталам. Важно правильно задать ширину и шаг столбцов, чтобы избежать перекрытия и сохранить читаемость графика.
Оптимизация трехмерной визуализации в Mathcad требует точного выбора типа графика, соответствующего характеру представляемых данных. Комбинирование различных представлений и грамотная настройка параметров визуализации повышает наглядность модели и упрощает интерпретацию сложных результатов расчетов.
Как построить 3D-график функции двух переменных
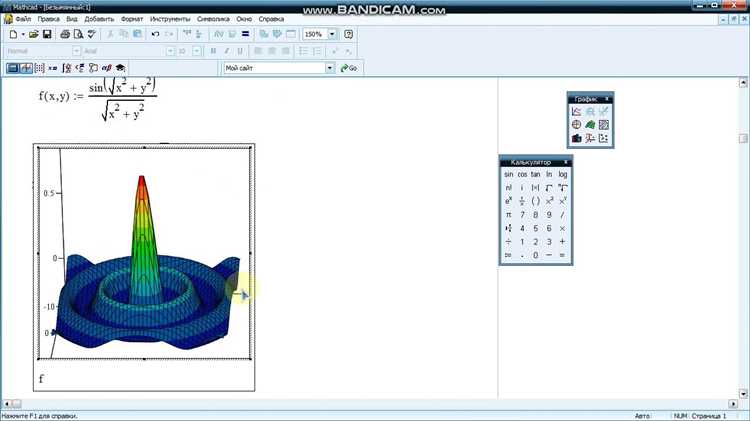
Для построения 3D-графика функции двух переменных в Mathcad необходимо выполнить следующие шаги:
1. Определите область определения переменных. Создайте два вектора значений для переменных x и y>. Например:
x := -10, -9.5 .. 10
y := -10, -9.5 .. 10
2. Постройте матрицу значений функции z = f(x, y). Используйте оператор вложенных циклов или функцию stack и augment для создания двумерной матрицы. Пример:
z := matrix(length(x), length(y))
for i ∈ 0..length(x)-1
for j ∈ 0..length(y)-1
z[i, j := sin(x[i]) * cos(y[j])
3. Вставьте график: используйте вставку 3D-графика через вкладку «Графики» – «3D-график».
4. Введите соответствующие выражения в поля осей: в поле X – x, в поле Y – y, в поле Z – z. Mathcad автоматически интерпретирует z как сетку значений по X и Y.
5. Настройте параметры отображения: можно включить сетку, изменить тип отображения (поверхность, проволочная модель), задать цветовую палитру, установить интервалы по осям.
Для корректного отображения размерности матрицы z должна соответствовать: количество строк – числу значений x, количество столбцов – числу значений y.
Настройка диапазонов осей X, Y и Z для объемных графиков
В Mathcad настройка диапазонов осей X, Y и Z для объемных графиков осуществляется непосредственно через свойства графика. Для этого дважды кликните по полю графика, чтобы открыть окно параметров.
Диапазон оси X задается параметрами X-min и X-max. Эти значения определяют минимальную и максимальную границу отображаемого участка. Например, при построении графика функции z = sin(x)·cos(y) в диапазоне x от –π до π необходимо указать X-min = –3.14, X-max = 3.14. Аналогично для оси Y.
Для корректного отображения трехмерной поверхности важно согласовать шаги сетки с диапазонами. Шаги определяются в разделе Grid → Number of Points. Например, для осей X и Y значения 50 или 100 обеспечат достаточную детализацию без избыточной нагрузки.
Ось Z отражает значения функции и требует отдельной настройки. Значения Z-min и Z-max задаются вручную или могут быть установлены автоматически, но ручная настройка позволяет исключить искажения при отображении. При построении графика с ожидаемым диапазоном z от –1 до 1 рекомендуется установить Z-min = –1.1 и Z-max = 1.1 для добавления визуального запаса.
Изменение масштаба по осям производится через флажки Log Scale, однако для объемных графиков логарифмический масштаб применяется ограниченно и только при положительных значениях переменных.
Чтобы сохранить пропорции графика, активируйте параметр Equal Axis Scaling. Это особенно важно при сравнении значений по разным осям, чтобы избежать визуальных искажений поверхности.
Настройка диапазонов осей – ключевой этап при построении объемных графиков в Mathcad, влияющий на точность визуального восприятия данных. Рекомендуется предварительно анализировать поведение функции на заданном интервале, чтобы задать оптимальные границы по каждой оси.
Использование цветовой заливки для визуализации высот

В Mathcad цветовая заливка поверхности используется для наглядного отображения изменения высот на трёхмерных графиках. Цветовая шкала кодирует значения по оси Z, позволяя быстро определить участки с максимальными и минимальными значениями. При построении графика типа surface (поверхность) активируйте параметр «Color Surface», чтобы включить заливку.
Для задания цветовой градации используется функция `colormap`. Mathcad поддерживает предопределённые схемы, например, `rainbow`, `thermal`, `grayscale`. Выбор схемы влияет на восприятие рельефа: тепловая палитра подчёркивает перепады, а градации серого подходят для аналитического анализа.
Цветовая интерполяция между узлами сетки регулируется плотностью данных. Чем выше разрешение матрицы значений, тем более точной будет визуализация. Рекомендуется использовать не менее 100×100 точек для сложных функций, чтобы избежать искажений цветовой заливки.
Пределы оси Z задаются вручную или автоматически. Для корректного отображения цвета важно установить фиксированный диапазон значений, особенно при сравнении нескольких графиков. Это делается через свойства осей: установите одинаковые минимумы и максимумы, чтобы обеспечить сопоставимость цветовой шкалы.
Используйте легенду (Color Bar) для количественной оценки высот. Она добавляется через настройки графика и должна быть размещена рядом с областью построения. Обязательно указывайте единицы измерения, если график представляет реальные величины.
При необходимости выделить определённые диапазоны значений применяйте пользовательские палитры через функцию `customcolormap`, указывая пороговые значения и соответствующие цвета. Это особенно полезно при анализе пороговых явлений, например, превышения температурных лимитов.
Отображение поверхностей с разрывами и особенностями
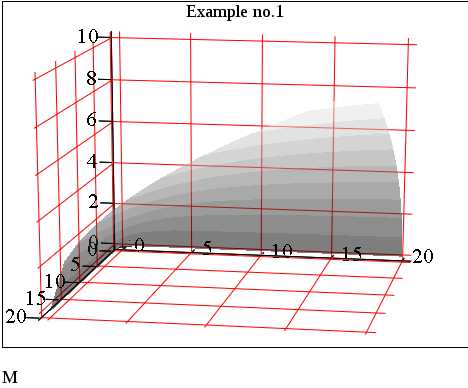
При построении трехмерных графиков в Mathcad важно учитывать поведение функции в областях с разрывами или особенностями. Такие участки часто возникают при делении на переменную, извлечении корня из отрицательных чисел или использовании логарифмов с недопустимыми аргументами.
Для корректного отображения поверхности с разрывами необходимо задать область определения явно. Используйте условные выражения, например if, для исключения недопустимых значений. Пример: if x≠0 then y/x else NaN. Значение NaN (Not a Number) сообщает Mathcad о невозможности построения точки, и она будет пропущена на графике, предотвращая искажение поверхности.
В случаях точечных особенностей (например, асимптот) рекомендуется использовать ограничение диапазона переменных: уменьшайте шаг дискретизации, избегайте включения границ с особенностями. Это повышает точность построения и устраняет артефакты визуализации.
Если особенности трудно локализовать, используйте функцию err или пользовательскую проверку условий в выражении для диагностики поведения функции. Это позволяет выявить зоны с нестабильными значениями до построения графика.
При визуализации резких переходов полезно изменять цветовую карту графика: в Mathcad можно задать цветовую зависимость от значения функции. Это позволяет выделить области с быстрым изменением значений или локальными экстремумами, которые часто сопровождают особенности поверхности.
Не следует пытаться «заполнить» разрывы: сглаживание может привести к ложной интерпретации данных. Поверхности с реальными особенностями лучше отображать с сохранением всех разрывов для достоверной визуализации поведения функции.
Как задать прозрачность и плотность сетки поверхности
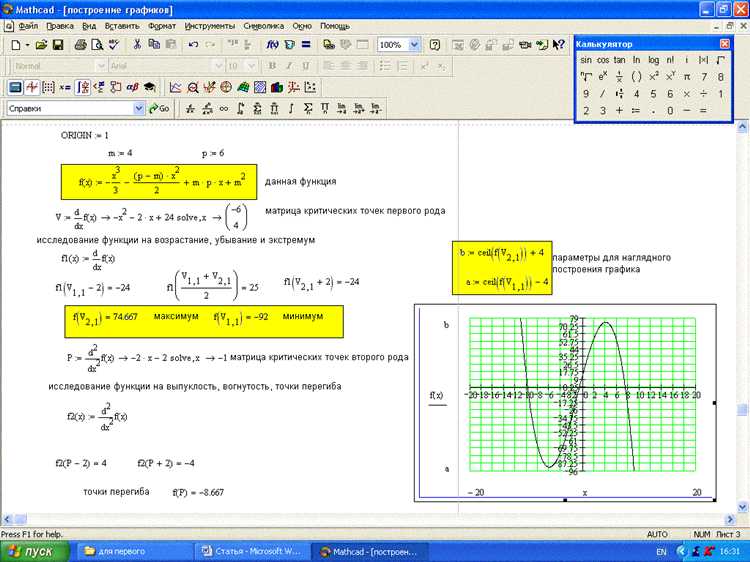
Для управления визуализацией 3D-графиков в Mathcad необходимо использовать свойства графического объекта. Эти параметры настраиваются через контекстное меню графика или в панели свойств.
- Прозрачность поверхности задаётся с помощью параметра Opacity в диапазоне от 0 до 1:
- 0 – полная прозрачность
- 1 – полная непрозрачность
- Рекомендуемое значение для частичной прозрачности: от 0.3 до 0.7
- Для изменения прозрачности:
- Щёлкните правой кнопкой по 3D-графику
- Выберите «Формат графика» → вкладка «Поверхность»
- Найдите параметр Opacity и задайте нужное значение вручную или с помощью ползунка
- Плотность сетки поверхности регулируется параметрами Grid X и Grid Y:
- Grid X – количество делений вдоль оси X
- Grid Y – количество делений вдоль оси Y
- Оптимальный диапазон: от 30 до 100 (зависит от детализации функции)
- Для настройки плотности:
- Откройте свойства 3D-графика
- Перейдите на вкладку «Сетка»
- Установите нужные значения в полях Grid X и Grid Y
Увеличение плотности сетки повышает детализацию поверхности, но может снизить производительность. Прозрачность облегчает восприятие внутренних структур в случае перекрывающихся элементов.
Сравнение графиков поверхности и контурных линий
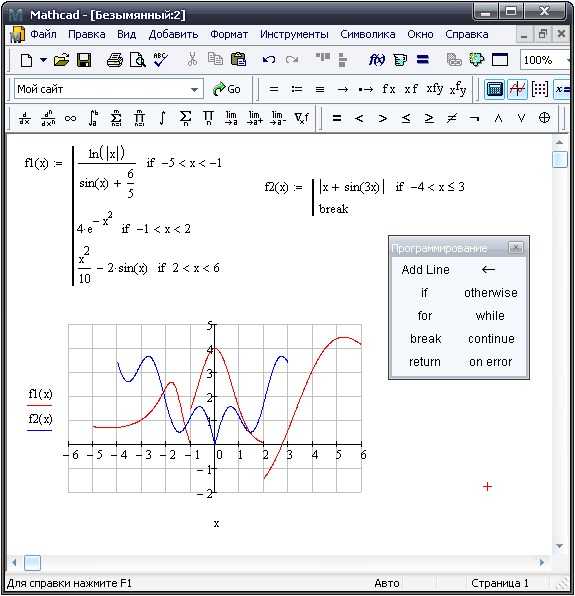
В Mathcad графики поверхности и контурные линии служат для визуализации функций двух переменных, однако имеют разные цели и особенности применения.
- Графики поверхности отображают трехмерную форму функции, где оси X и Y – независимые переменные, а ось Z – значение функции. Они позволяют сразу увидеть общий рельеф и объемную структуру.
- Контурные линии представляют проекцию уровня функции на плоскость XY. Каждая линия соответствует фиксированному значению Z, что упрощает анализ изменений функции по высоте.
При выборе между этими типами графиков стоит учитывать следующие моменты:
- Для оценки глобальных особенностей поверхности (например, выпуклости, впадин, седловых точек) предпочтительнее график поверхности.
- Для точного определения уровней функции и анализа зон с одинаковыми значениями лучше использовать контурные линии, особенно когда важно сравнить высоты без трехмерного искажения.
- Контурные линии удобны для сложных функций с большим количеством локальных экстремумов, поскольку они наглядно показывают распределение уровней, не перегружая визуализацию.
- Графики поверхности требуют более мощного аппаратного обеспечения и могут быть менее информативны при плотном расположении данных, тогда как контурные линии более экономичны и читаемы при большом объеме данных.
- В Mathcad возможно совмещение этих типов, что расширяет аналитические возможности: трехмерная поверхность дополняется контурными линиями на основании, усиливая понимание структуры функции.
Рекомендации по использованию в Mathcad:
- Для начального анализа данных лучше строить график поверхности, чтобы получить общее представление.
- Для детального изучения распределения уровней и сравнений применяйте контурные линии с выбором разумного количества уровней, чтобы избежать перегрузки.
- Используйте параметры визуализации Mathcad, такие как прозрачность поверхности и цветовые схемы контуров, для повышения читаемости комбинированных графиков.
- При сложных функциях с резкими изменениями рекомендуется одновременно использовать оба типа графиков, что поможет выявить ключевые особенности и структурные закономерности.
Построение пространственных траекторий и кривых
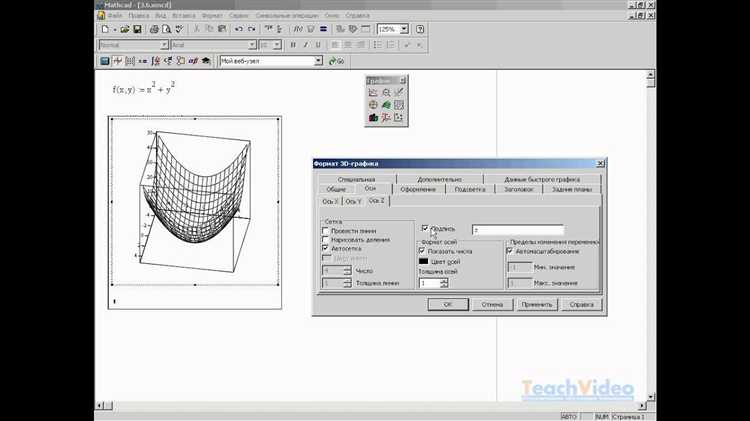
Для создания пространственных траекторий в Mathcad применяется параметрическое задание кривых через три функции координат X(t), Y(t) и Z(t). Параметр t обычно задается в пределах заданного диапазона, обеспечивая непрерывность и гладкость кривой.
Рекомендуется использовать встроенную функцию plot3d с параметрическим режимом, где задаются три одномерные функции, соответствующие координатам в зависимости от параметра t. Для точного отображения важен выбор количества точек дискретизации: минимум 100-200 точек обеспечивают плавность, но при больших вычислительных задачах можно уменьшать этот параметр.
При необходимости анализа кривой в пространстве полезно дополнительно визуализировать касательные и нормальные векторы, что в Mathcad достигается расчетом производных функций координат и добавлением векторных объектов на график.
Для построения сложных траекторий, таких как спирали, циклоиды или линии пересечения поверхностей, следует применять соответствующие аналитические формулы и задавать параметр t с учетом физических или геометрических ограничений. Mathcad позволяет легко изменять диапазон и шаг параметра, что ускоряет оптимизацию визуализации.
Для контроля точности графика рекомендуется периодически сверять координаты ключевых точек кривой с вычисленными значениями, особенно при использовании нелинейных или кусочно-заданных функций.
Импорт табличных данных для построения 3D-графика
Для создания трехмерного графика в Mathcad данные должны быть структурированы в виде трехмерной матрицы или наборов координатных векторов. Оптимальный формат – CSV-файл с разделением значений по строкам и столбцам, где первая строка содержит заголовки, а последующие – числовые значения.
Импорт начинается с команды вставки данных через меню «Вставка» → «Таблица» или с использованием встроенных функций чтения файлов, таких как READPRN() или READCSV(). После загрузки необходимо проверить корректность диапазонов и типов данных, так как Mathcad строго требует числовой формат для построения 3D-графиков.
Для формирования трехмерного массива координат X, Y и соответствующих значений Z обычно применяют функцию reshape(), если данные импортированы в плоском виде. Важно следить, чтобы размерности совпадали: длина векторов X и Y должна соответствовать размеру сетки Z.
При работе с неструктурированными наборами данных рекомендуется предварительно преобразовать их в регулярную сетку с помощью интерполяции, например, функции interp2(), чтобы обеспечить равномерное распределение точек и избежать искажений графика.
Визуализация 3D-графика в Mathcad осуществляется через функцию surface() или mesh(), которые принимают на вход матрицы X, Y и Z. Для улучшения читаемости можно настроить параметры отображения, например, цветовую палитру и уровень детализации.
Вопрос-ответ:
Какие основные типы трехмерных графиков можно построить в Mathcad?
В Mathcad доступны несколько основных видов трехмерных графиков: поверхности (3D Surface), контурные графики (Contour plots), а также точечные и линейные трехмерные графики. Поверхности отображают функцию двух переменных, контурные графики показывают линии равного значения функции на плоскости, а точечные и линейные графики позволяют визуализировать отдельные точки и соединяющие их линии в пространстве.
Как в Mathcad задать параметры осей для трехмерного графика?
Для настройки осей в трехмерных графиках Mathcad предоставляет возможность вручную задавать диапазоны значений по каждой оси X, Y и Z. Это делается через свойства графика, где можно указать минимальные и максимальные значения, а также шаг сетки. Настройка помогает сфокусироваться на интересующем участке данных и улучшить восприятие визуализации.
Можно ли в Mathcad комбинировать несколько типов трехмерных графиков на одном рисунке?
Да, Mathcad позволяет объединять разные типы трехмерных графиков в одном окне. Например, можно совместить поверхность с точечным графиком, чтобы дополнительно выделить важные точки на поверхности. Для этого необходимо добавить несколько графических элементов и настроить их отображение в одном 3D-пространстве.
Какие возможности по изменению визуального стиля трехмерных графиков есть в Mathcad?
В Mathcad можно изменять цветовую гамму, прозрачность и тип отображения поверхности или линий. Например, поверхность может быть заполнена цветом с градиентом, либо отображаться в виде сетки. Можно также регулировать толщину линий и размер точек, что помогает выделить нужные детали на графике и сделать изображение более информативным и понятным.
Как построить трехмерный график функции с несколькими переменными в Mathcad?
Для построения трехмерного графика функции двух переменных в Mathcad нужно сначала определить функцию, которая принимает два аргумента (обычно X и Y), а затем использовать встроенный инструмент трехмерного графика, который отображает значения функции по оси Z. Важно правильно задать диапазоны для X и Y и обеспечить достаточное количество точек сетки, чтобы график получился плавным и точным.
Какие основные типы трехмерных графиков можно построить в Mathcad и в чем их различия?
В Mathcad доступны несколько основных типов трехмерных графиков: поверхностные графики (surface plots), графики точек (scatter plots) и графики линий (3D line plots). Поверхностные графики отображают зависимость одной переменной от двух других с помощью сетки, создавая объемную поверхность. Графики точек представляют собой набор дискретных точек в трехмерном пространстве, что полезно для анализа выборок. Графики линий показывают траектории или зависимости, соединяя точки линиями в трехмерном пространстве. Выбор типа зависит от задачи: для визуализации функции – surface plot, для демонстрации экспериментальных данных – scatter plot, а для отображения путей или зависимостей – 3D line plot.