
Транспонирование матрицы – это операция, при которой строки матрицы становятся столбцами, а столбцы – строками. В Python существует несколько эффективных способов выполнения этой операции, каждый из которых может быть полезен в зависимости от ситуации. Транспонирование широко применяется в математике, машинном обучении и обработке данных, особенно при работе с многомерными массивами, которые требуют манипуляций с их формой.
Один из самых быстрых и простых способов транспонирования матрицы – использование библиотеки NumPy. Эта библиотека предоставляет встроенную функцию numpy.transpose() для работы с многомерными массивами. Важно отметить, что NumPy обеспечивает высокую производительность, что критично при работе с большими объемами данных. Например, вызов matrix.T или numpy.transpose(matrix) позволяет транспонировать массив за одну операцию, что является предпочтительным методом в большинстве случаев.
Если задача не требует использования сторонних библиотек, транспонирование можно реализовать с помощью стандартных средств Python. Например, при работе с вложенными списками можно использовать функцию zip() вместе с распаковкой аргументов. Этот способ менее эффективен по скорости, но может быть полезен в учебных целях или в случае небольших матриц.
В этой статье рассмотрим различные способы транспонирования матриц в Python, их особенности и различия в производительности, чтобы выбрать оптимальный метод для решения конкретных задач.
Использование метода.T для транспонирования в NumPy

Метод .T работает с объектами типа numpy.ndarray и просто изменяет ориентацию данных: строки становятся столбцами, а столбцы – строками. Важно отметить, что транспонирование с помощью .T не создаёт копию исходной матрицы, а возвращает представление данных с изменённой ориентацией. Это позволяет экономить память при работе с большими массивами данных.
Пример использования:
import numpy as np
matrix = np.array([[1, 2, 3], [4, 5, 6]])
transposed_matrix = matrix.T
print(transposed_matrix)Результатом работы этого кода будет матрица:
[[1 4]
[2 5]
[3 6]]Метод .T работает не только с двухмерными массивами, но и с многомерными, предоставляя аналогичные результаты для транспонирования каждого измерения массива. Для многомерных массивов можно использовать .swapaxes(), если требуется транспонирование конкретных осей, однако .T остаётся удобным инструментом для базовых операций.
При работе с большими массивами важно помнить, что .T не создаёт копию данных, а лишь меняет представление. Это гарантирует быстрые вычисления и минимальное использование памяти, что особенно полезно при работе с массивами размером в несколько миллионов элементов.
Метод .T является частью стандартного функционала NumPy и подходит для большинства случаев, требующих транспонирования данных. Однако, если вам нужно произвести более сложные манипуляции с осями, рекомендуется рассмотреть использование функций swapaxes или transpose, которые предоставляют дополнительные возможности.
Транспонирование матрицы с помощью list comprehension
Для транспонирования матрицы в Python можно использовать list comprehension, что позволяет сделать код более компактным и читаемым. Метод заключается в том, чтобы для каждой строки исходной матрицы сформировать столбец в новой матрице.
Пример транспонирования матрицы с использованием list comprehension:
matrix = [ [1, 2, 3], [4, 5, 6], [7, 8, 9] ] transposed = [[matrix[j][i] for j in range(len(matrix))] for i in range(len(matrix[0]))] print(transposed)
В этом примере:
matrix– исходная матрица, состоящая из 3 строк и 3 столбцов.transposed– новая матрица, полученная в результате транспонирования.- Внешний цикл
for i in range(len(matrix[0]))итерирует по индексам столбцов исходной матрицы, а внутренний циклfor j in range(len(matrix))проходит по строкам.
Такой способ эффективно обрабатывает матрицы любой размерности, и благодаря list comprehension код остаётся коротким и понятным.
Важно помнить, что в этом примере предполагается, что все строки матрицы имеют одинаковую длину. Для работы с матрицами разной длины строк потребуется дополнительная обработка, например, проверка на пустые элементы.
Преимущества использования list comprehension для транспонирования:
- Компактность кода.
- Улучшенная читаемость по сравнению с обычными циклами.
- Высокая производительность при небольших и средних размерах матриц.
Метод удобен для работы с небольшими и средними матрицами. Для очень больших матриц рекомендуется использовать другие подходы, такие как библиотеки NumPy, которые оптимизированы для работы с массивами данных и поддерживают операцию транспонирования напрямую.
Как транспонировать матрицу с использованием цикла for
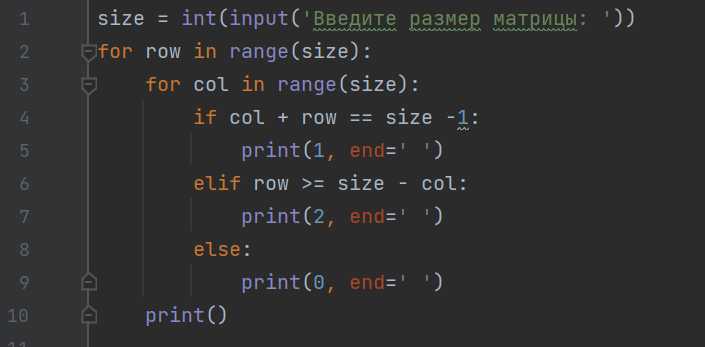
Предположим, у нас есть матрица, представляемая списками в Python:
matrix = [ [1, 2, 3], [4, 5, 6], [7, 8, 9] ]
Чтобы транспонировать такую матрицу, нужно сформировать новую матрицу, в которой первый столбец исходной матрицы станет первой строкой, второй столбец – второй строкой и так далее.
Реализуем транспонирование с помощью цикла for. Для этого создадим пустую матрицу transpose, в которую будем добавлять строки, сформированные из столбцов исходной матрицы.
transpose = [] for i in range(len(matrix[0])): # Количество столбцов row = [] for j in range(len(matrix)): # Количество строк row.append(matrix[j][i]) # Добавляем элементы столбца в строку transpose.append(row) # Добавляем строку в транспонированную матрицу
После выполнения этого кода матрица transpose будет выглядеть так:
[ [1, 4, 7], [2, 5, 8], [3, 6, 9] ]
Здесь первый столбец исходной матрицы стал первой строкой транспонированной матрицы, второй столбец – второй строкой, и так далее. Этот метод наглядно и понятно выполняет задачу транспонирования с использованием стандартных средств Python.
Для того чтобы избежать ошибок с индексами, важно убедиться, что количество строк и столбцов правильно учтено в цикле. Также данный способ эффективно работает даже для матриц с различным числом строк и столбцов, не обязательно квадратных.
Транспонирование матрицы с помощью функции zip()
Для транспонирования матрицы с помощью zip() достаточно передать в нее строки матрицы как отдельные аргументы. Например, если у нас есть матрица в виде списка списков, каждый внутренний список будет представлять строку матрицы. После применения zip(), каждый столбец исходной матрицы становится строкой новой, транспонированной матрицы.
Пример кода:
matrix = [
[1, 2, 3],
[4, 5, 6],
[7, 8, 9]
]
transposed = list(zip(*matrix))
print(transposed)
Результат:
[(1, 4, 7), (2, 5, 8), (3, 6, 9)]
Важно, что при использовании zip() исходные строки передаются через оператора распаковки *. Это позволяет передать все строки матрицы как отдельные аргументы в функцию. Результатом работы zip() является итератор, который необходимо преобразовать в список с помощью list(), чтобы получить транспонированную матрицу.
Такой подход удобен для работы с матрицами, представленных списками, и позволяет эффективно транспонировать данные без необходимости использования дополнительных библиотек.
Работа с большими матрицами: оптимизация использования памяти
Одним из ключевых аспектов является выбор типа данных для хранения матрицы. Например, для хранения чисел с плавающей запятой можно использовать тип float32 вместо float64, что уменьшит объём памяти в два раза без существенной потери точности в большинстве случаев. В NumPy можно указать тип данных при создании массива с помощью параметра dtype.
Ещё одним методом оптимизации является использование разреженных матриц. Если матрица содержит большое количество нулевых элементов, можно применить структуры данных, такие как scipy.sparse, которые эффективно хранят только ненулевые элементы. Это позволяет значительно уменьшить объём памяти при работе с такими матрицами.
Для временных результатов и промежуточных вычислений лучше использовать векторизованные операции. В NumPy и SciPy такие операции обычно выполняются напрямую на массиве, минимизируя количество промежуточных объектов и экономя память. Важно избегать использования лишних копий массивов, а вместо этого использовать методы, которые изменяют данные на месте, например, inplace методы в NumPy.
Другим вариантом оптимизации является использование генераторов для поочерёдной обработки элементов матрицы. Это позволяет работать с матрицами, которые не помещаются в оперативную память целиком, путём загрузки и обработки данных по частям. В Python для этого можно использовать generator expressions.
Наконец, следует учитывать, что размер матрицы и её структура могут сильно влиять на производительность и использование памяти. Для очень больших матриц может быть полезно использовать методы работы с матрицами на диске, такие как memory-mapped files с помощью numpy.memmap, что позволяет загружать данные из файла непосредственно в память, без необходимости хранить их в оперативной памяти.
Проверка корректности транспонирования матрицы в Python
Для проверки корректности транспонирования матрицы в Python необходимо убедиться, что после транспонирования строки становятся столбцами, а столбцы – строками. Важно, чтобы размерность исходной и транспонированной матрицы соответствовала друг другу: если матрица была размером m x n, то транспонированная должна быть размером n x m.
Простой способ проверки – сравнение транспонированной матрицы с результатом транспонирования с использованием различных методов. Рассмотрим несколько проверок:
1. Использование циклов для проверки
Можно пройти по строкам и столбцам и убедиться, что элементы транспонированной матрицы соответствуют ожиданиям. Например, если исходная матрица имеет размер m x n, то после транспонирования элемент с индексом [i][j] должен быть равен элементу с индексом [j][i] исходной матрицы.
2. Использование библиотеки NumPy
Библиотека NumPy предоставляет удобный способ для транспонирования матриц и проверки корректности. Для этого можно транспонировать матрицу и затем сравнить результат с ожиданиями. Пример:
import numpy as np matrix = np.array([[1, 2, 3], [4, 5, 6]]) transposed = matrix.T Проверка: элемент [i][j] в исходной матрице должен быть равен элементу [j][i] в транспонированной assert np.all(matrix.T == transposed)
3. Сравнение с вручную транспонированной матрицей
Если транспонирование выполнено вручную, можно создать аналогичную матрицу и сравнить элементы. Важно учитывать, что при транспонировании индексы меняются местами, например, элемент на позиции [0][1] исходной матрицы должен переместиться на позицию [1][0] в транспонированной матрице.
4. Тестирование с разными размерами матриц
Необходимо проверять как квадратные матрицы, так и прямоугольные (в том числе, матрицы с одной строкой или одним столбцом). Например, транспонирование матрицы 1 x 3 должно возвращать матрицу 3 x 1, а транспонирование матрицы 3 x 1 – матрицу 1 x 3.
5. Обработка ошибок
Также важно предусмотреть обработку ошибок, если матрица имеет неправильные размеры или данные, что может привести к неверным результатам при транспонировании. Например, если передать не матрицу (например, список с разной длиной вложенных списков), то транспонирование вызовет ошибку. Нужно заранее проверять, что входные данные представляют собой корректную матрицу.






