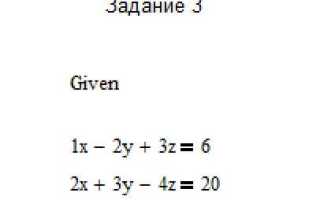Как посчитать уравнение в mathcad

Mathcad предоставляет мощные инструменты для решения алгебраических и дифференциальных уравнений благодаря встроенным функциям численного и аналитического анализа. Для численного решения уравнений в Mathcad применяются методы итераций, такие как метод Ньютона, который реализуется через функцию root(). Она позволяет найти корни нелинейных уравнений с точностью, задаваемой пользователем.

Для работы с системами уравнений рекомендуется использовать векторное и матричное представление, что упрощает запись и повышает скорость вычислений. В Mathcad важно корректно задавать начальные приближения – их выбор напрямую влияет на сходимость метода и точность результата.

При решении дифференциальных уравнений применяется встроенный численный интегратор rkfixed(), основанный на методе Рунге-Кутты. Важно грамотно определить начальные условия и интервал решения для получения устойчивого и корректного результата.

Подготовка уравнения для решения в Mathcad

Перед вводом уравнения в Mathcad необходимо убедиться, что оно записано в аналитической форме с четким определением всех переменных. Важный момент – однозначное обозначение всех параметров и функций, чтобы избежать конфликтов с встроенными командами программы.

Mathcad воспринимает уравнения как выражения с присвоением или равенством. Для решения задается уравнение с оператором равенства «=», а неизвестные переменные должны быть явно указаны. Пример: f(x) = x^2 — 4.

Следует использовать точную синтаксис Mathcad для операций, например, оператор возведения в степень обозначается ^, а не **. Дробные выражения вводятся с использованием косой черты «/», причем скобки применяются для корректного порядка вычислений.

Необходимо задать начальные приближения или интервал для решения, если уравнение не является линейным. Mathcad решает численно уравнения с помощью функции solve или оператора root, поэтому важно подготовить область поиска корня.

Если уравнение содержит производные, то их надо оформлять в Mathcad через оператор производной (например, prime: f′(x)), а интегралы задаются встроенными функциями. Для систем уравнений переменные указываются списком, а каждое уравнение записывается отдельно, чтобы обеспечить корректную работу решателя.

Нельзя использовать неинициализированные переменные. Все параметры, участвующие в уравнении, должны иметь числовые значения или быть объявлены как параметры с фиксированными значениями до запуска решения.

Использование встроенных функций для численного решения уравнений

Mathcad предлагает несколько встроенных функций для численного решения уравнений, среди которых root и solve занимают ключевое место. Функция root применяется для поиска корней одной переменной в уравнении, задаваемом в виде выражения. Важно указать начальное приближение, поскольку метод опирается на итерационный процесс, чувствительный к выбору стартового значения.

Для решения систем уравнений удобно использовать функцию solve, позволяющую задавать несколько выражений одновременно. Решение возвращается в виде вектора, что упрощает дальнейшую обработку результатов. При этом рекомендуется явно определить переменные как искомые, а уравнения – в виде равенств с нулём.

В Mathcad также доступна функция Find для поиска корней с дополнительными параметрами, позволяющими ограничивать область поиска и задавать точность решения. Для повышения устойчивости вычислений полезно комбинировать эту функцию с анализом графиков, позволяющим визуально оценить поведение функции и уточнить начальные приближения.

Практический совет: для повышения точности решения необходимо учитывать свойства исходного уравнения, избегая областей с резкими изменениями или разрывами. Рекомендуется проводить проверку полученных корней через подстановку в исходное уравнение и оценку погрешности.

Решение систем уравнений с помощью Mathcad

Mathcad позволяет решать системы уравнений численными и аналитическими методами, обеспечивая гибкий подход к различным задачам.

1. Задание системы уравнений:
   • Используйте оператор «:=» для определения уравнений, например: eq1 := x + y = 5, eq2 := 2*x - y = 3.
   • Для удобства объедините уравнения в вектор или список, например: system := [eq1, eq2].
2. Аналитическое решение:
   • Вызовите функцию solve() с указанием переменных: solve(system, [x,y]).
   • Mathcad возвращает решение в виде набора значений переменных, если оно существует.
   • Для систем с линейными уравнениями можно использовать матричный подход: задайте матрицу коэффициентов и вектор свободных членов, примените оператор обратной матрицы.
3. Численное решение:
   • Если система нелинейная или аналитическое решение невозможно, используйте функцию Find.
   • Задайте начальное приближение переменных: guess := [x0, y0].
   • Вызовите Find(system, guess) для вычисления численных корней.
   • Проверьте сходимость решения, изменяя начальное приближение при необходимости.
4. Особенности и рекомендации:
   • Для систем с большим числом уравнений используйте векторы и матрицы вместо множества отдельных переменных.
   • Проверяйте корректность введённых уравнений – Mathcad чувствителен к синтаксису и знакам равенства.
   • Используйте встроенные функции для преобразования и упрощения уравнений перед решением.
   • Для параметрических систем задавайте параметры отдельно и анализируйте поведение решений при их изменении.

Настройка параметров точности и ограничений при решении

В Mathcad точность решения уравнений напрямую зависит от параметров, задаваемых в блоках решения. Для численных методов точность определяется параметром tolerance, который задаёт максимально допустимую погрешность. Рекомендуется устанавливать значение tolerance в диапазоне от 1e-6 до 1e-12 в зависимости от требуемой точности и вычислительных ресурсов.

Параметр max iterations ограничивает количество итераций, выполняемых алгоритмом. По умолчанию значение часто составляет 100, но для уравнений с медленной сходимостью целесообразно увеличить этот лимит до 500 или более. Это помогает избежать преждевременного прерывания вычислений.

Важно учитывать начальные приближения. Они существенно влияют на сходимость и стабильность решения. Для нелинейных уравнений стоит задавать начальное значение близкое к ожидаемому корню, иначе метод может выйти за границы определения функции.

В Mathcad можно задавать ограничения на переменные с помощью условных выражений. Это особенно полезно при решении систем уравнений с физическими или техническими ограничениями. Например, если переменная должна быть положительной, необходимо прописать условие x > 0 прямо в блоке уравнений.

При сложных задачах следует использовать функцию FindRoot с указанием дополнительных параметров точности и ограничения по времени выполнения. Установка параметра timeout помогает избежать бесконечных циклов в случае отсутствия сходимости.

Настройка параметров должна учитывать баланс между точностью и временем решения: чрезмерно жёсткие требования могут значительно увеличить вычислительные затраты без ощутимого выигрыша в результате.

Анализ и проверка полученных решений в Mathcad

После решения уравнения в Mathcad важно проверить корректность результата. Для этого следует использовать встроенные функции подстановки и численной оценки. Например, подставьте найденное значение обратно в исходное уравнение с помощью оператора присваивания и функции численного вычисления, чтобы убедиться, что выражение стремится к нулю или другому ожидаемому значению.

Если уравнение имеет несколько решений, рекомендуется провести визуальный анализ с помощью графиков. Постройте функцию левой и правой части уравнения в одном окне, отметьте точки пересечения для оценки совпадения. Это помогает обнаружить ошибки в пределах области определения и исключить посторонние корни.

При использовании численных методов, таких как root() или find(), задавайте начальные приближения и контролируйте сходимость. Оцените погрешность решения, сравнивая результаты при различных методах или повторных запусках с изменёнными параметрами.

Резюмируя, систематическая проверка через подстановку, численную оценку, графический анализ и параметрическое исследование обеспечивает уверенность в корректности решения, исключая ложные корни и ошибки округления.

Типичные ошибки при решении уравнений и способы их устранения

Неправильное задание уравнения. В Mathcad важно точно формулировать уравнение, учитывая синтаксис. Часто встречается ошибка при использовании знаков равенства: вместо оператора сравнения (=) следует применять функцию = внутри выражений или использовать оператор solve. Чтобы исправить, проверяйте, что уравнение имеет формат f(x)=0, а не присваивания.

Отсутствие начальных приближений для численных методов. Для методов, таких как root или solve, Mathcad требует стартового значения. Без него решение может не найдется или будет неверным. Всегда задавайте реалистичное приближение, исходя из анализа уравнения, чтобы повысить вероятность сходимости.

Несогласованность единиц измерения. Mathcad автоматически учитывает единицы, но ошибки появляются, если части уравнения имеют разные или несовместимые единицы. Перед решением убедитесь, что все величины приведены к единой системе.

Игнорирование ограничений области определения. Решение может быть некорректным, если переменная выходит за допустимый диапазон. Устанавливайте ограничения явно с помощью функций when или проверяйте область значений переменной, чтобы избежать лишних корней.

Неверное использование встроенных функций. Mathcad имеет свои особенности в определении функций и операторов. Например, не стоит путать оператор := для определения функций с обычным знаком равенства. Правильное определение функции обеспечивает корректный расчет при решении.

Отсутствие проверки результата. После нахождения корня подставьте его обратно в уравнение. Если значение функции существенно отличается от нуля, решение недостоверно. В таких случаях попробуйте изменить начальное приближение или пересмотреть постановку задачи.

Вопрос-ответ:

Как задать уравнение для решения в Mathcad?

Чтобы решить уравнение в Mathcad, сначала необходимо записать его в виде выражения с использованием переменных и знаков равенства. Затем укажите переменную, которую хотите найти, и используйте функцию решения, например, `solve` или оператор равенства для численного метода. Важным шагом является правильное определение всех параметров и условий задачи, чтобы программа могла корректно обработать уравнение.

Можно ли решать одновременно несколько уравнений в Mathcad?

Да, Mathcad позволяет решать системы уравнений. Для этого следует записать каждое уравнение отдельно и объединить их в систему, указав переменные для поиска. Затем примените функцию решения системы, которая вернет значения всех переменных, удовлетворяющих всем уравнениям. При этом желательно задавать начальные приближения для численных методов, чтобы ускорить поиск решения и избежать ошибок.

Что делать, если Mathcad не находит решение уравнения?

Если решение не находится, стоит проверить правильность записи уравнения и заданных условий. Иногда проблема связана с отсутствием начального приближения или с тем, что уравнение не имеет корней в реальном виде. Можно попробовать изменить метод решения, задать диапазон поиска или упростить уравнение. Также полезно проверить, нет ли синтаксических ошибок в записи или конфликтов в определении переменных.

Какие типы уравнений поддерживает Mathcad для решения?

Mathcad способен работать с разными типами уравнений: алгебраическими, трансцендентными, дифференциальными и даже системами уравнений. Для каждого типа существуют соответствующие инструменты и функции, которые позволяют получить численные или аналитические решения. Например, для дифференциальных уравнений используются специальные операторы, а для алгебраических — стандартные функции решения. Важно понимать специфику задачи и выбирать подходящий способ решения.