Построение графиков комплексных функций в Mathcad требует понимания как самой природы комплексных чисел, так и возможностей системы визуализации. В отличие от действительных функций, значения комплексных отображений невозможно напрямую отобразить на плоскости XY. Поэтому в Mathcad используется способ раздельного представления модуля и аргумента функции.
Для анализа поведения функции f(z), где z = x + iy, целесообразно зафиксировать одну переменную и рассматривать изменение другой. Один из распространённых подходов – построение графика модуля |f(z)| по сетке действительных и мнимых частей z. Это реализуется через матричное задание переменных и последующее построение поверхности или контурного графика.
В Mathcad удобно использовать функцию surface plot для отображения модуля |f(x + iy)|. Для этого создаются два массива: один для действительной части x, другой – для мнимой y. Затем формируется двумерная матрица значений функции. В случае, если требуется анализ аргумента arg(f(z)), строится отдельный график на основе функции atan2, обеспечивающей корректное определение угла в комплексной плоскости.
При построении важно учитывать особенности отображаемой функции: наличие особенностей, точек ветвления, зон с резким изменением модуля или аргумента. Mathcad предоставляет достаточно инструментов для точного и наглядного представления этих особенностей, особенно при использовании плотных сеток и цветового кодирования уровней.
Настройка рабочей области Mathcad для комплексных переменных
Для корректной работы с комплексными переменными в Mathcad необходимо задать соответствующий формат отображения и вычислений. Откройте вкладку «Math» в панели параметров документа и активируйте опцию «Display Imaginary Unit as i», чтобы обозначение мнимой единицы соответствовало принятому математическому стандарту.
В разделе «Calculation» установите режим «Automatic» для мгновенного пересчёта выражений при изменении параметров. Убедитесь, что включена опция «Complex Results», иначе выражения с комплексными компонентами будут упрощаться до действительных, если это возможно, что исказит результат.
При вводе комплексных переменных используйте стандартную форму: например, z := 3 + 4i. Mathcad распознаёт литерал i как мнимую единицу только при отсутствии конфликта с определёнными переменными. Не используйте i в качестве имени переменной.
Для визуализации комплексных функций создавайте массивы значений с использованием диапазонов: x := -10, -9.9 .. 10 и y := -10, -9.9 .. 10. Затем определите комплексную сетку Z := x + i·y через функцию augment или вложенные циклы for, чтобы обеспечить двумерную структуру данных.
Перед построением графиков убедитесь, что панель инструментов «3D Plot» активна. В свойствах графика укажите оси X и Y по действительной и мнимой части, а Z – по модулю, фазе или действительной/мнимой части функции. Используйте функции abs() и arg() для анализа комплексной величины.
Определение комплексной функции с помощью встроенных операторов
Mathcad позволяет определять комплексные функции напрямую, используя встроенные операторы и поддержку комплексной арифметики. Для задания комплексной переменной используется конструкция z := x + i·y, где i – мнимая единица, а x и y – действительные переменные.
Комплексные функции определяются как обычные выражения, в которых аргумент – комплексная переменная. Например, функция f(z) := z² + exp(i·z) будет автоматически интерпретироваться как комплексная, без необходимости дополнительных указаний.
Для использования стандартных функций с комплексными аргументами применяются те же имена, что и для действительных чисел: sin(z), ln(z), abs(z), arg(z), Re(z), Im(z). Mathcad корректно обрабатывает ветвления многозначных функций, например, логарифма и корня.
Пример определения:
z := x + i·y f(z) := ln(z) + z²
Для корректной работы функции на множестве значений необходимо задавать x и y как диапазоны, после чего использовать вложенные операторы vectorize и map для покоординатной обработки.
Рекомендуется избегать ручного разбиения на действительную и мнимую части, так как встроенные операторы автоматически управляют вычислениями и обеспечивают корректность результатов на всей комплексной плоскости.
Выбор диапазона и дискретизации комплексной переменной
Для построения графика комплексной функции в Mathcad необходимо определить прямоугольную область на комплексной плоскости. Пусть комплексная переменная z представляется в виде z = x + iy, где x и y – действительные переменные. Задаются два вектора: x := lin(x₀, x₁, N) и y := lin(y₀, y₁, M), где lin – встроенная функция линейного распределения, x₀ и y₀ – нижние границы, x₁ и y₁ – верхние границы, N и M – количество точек дискретизации.
Чем выше значения N и M, тем точнее визуализация, но увеличивается нагрузка на память. Оптимальное значение: от 100 до 300 точек по каждой оси. Для функций с резкими переходами или особенностями рекомендуется использовать не менее 500 точек.
Создание сетки выполняется через оператор z(x, y) := x + i·y, где x и y – матрицы, полученные с помощью функции augment и транспонирования. Пример: X := augment(x), Y := augment(y)ᵗ. Затем Z := X + i·Y.
Диапазон должен охватывать область, в которой функция демонстрирует интересное поведение: особенности, полюса, ветвления. Например, для анализа функции f(z) = 1/(z² + 1) диапазон x, y ∈ [-2, 2] позволяет визуализировать особенности в окрестности мнимых единиц.
Следует избегать слишком широких диапазонов без необходимости – это приводит к размытию деталей. При необходимости концентрировать внимание на локальных особенностях – использовать масштабирование области и увеличивать плотность сетки.
Преобразование комплексной функции в модуль и аргумент для отображения
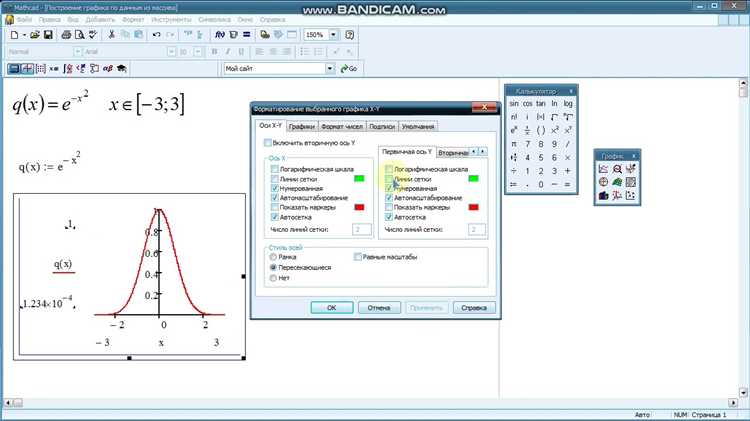
Для построения графика комплексной функции в Mathcad требуется преобразовать её в форму, пригодную для визуализации. Комплексные значения нельзя отобразить напрямую на плоскости, поэтому используется разложение на модуль и аргумент.
- Модуль комплексной функции вычисляется через выражение
|f(z)| = sqrt(Re(f(z))² + Im(f(z))²). В Mathcad это записывается какabs(f(z)). - Аргумент (фаза) определяется через функцию
arg(f(z)) = atan2(Im(f(z)), Re(f(z))). В Mathcad используетсяarg(f(z)), которая автоматически возвращает значение в радианах.
Для корректного отображения необходимо задать двумерную сетку значений переменной z. Например:
x := linspace(-5, 5, 100)
y := linspace(-5, 5, 100)
z := x + i·y^T
Далее вычисляются значения функции, модуля и аргумента:
f_z := f(z)
mod_f := abs(f_z)
arg_f := arg(f_z)
Для построения используется функция surfaceplot или contourplot:
surfaceplot(x, y, mod_f)– визуализация модуля.contourplot(x, y, arg_f)– отображение фазовых линий.
Аргумент часто нормируют в диапазон от -π до π для получения корректной цветовой схемы. При необходимости – использовать выражение mod(arg_f + π, 2·π) - π.
Такая декомпозиция даёт два независимых представления: амплитудное (модуль) и фазовое (аргумент), что критично при анализе особенностей поведения функции, в том числе особенностей, нулей и полюсов.
Использование функции surface plot для визуализации модуля
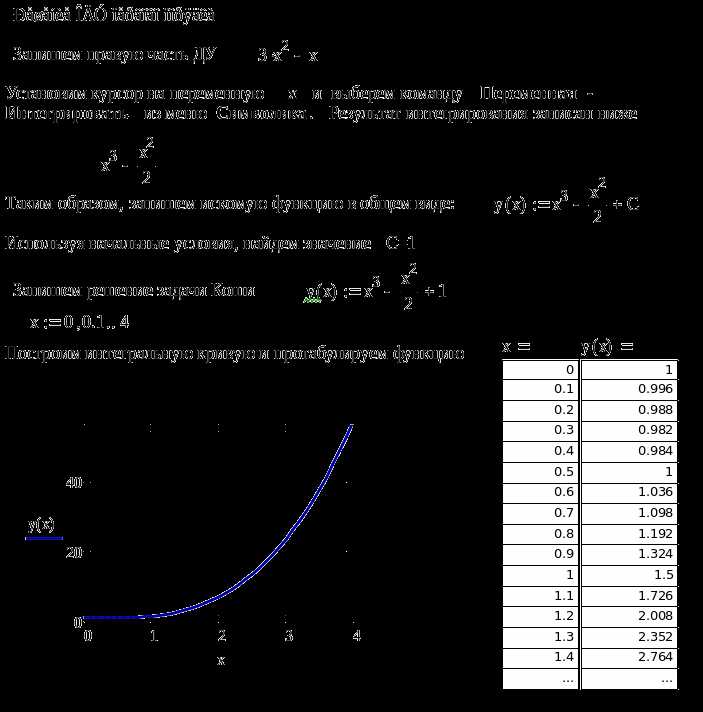
Для построения графика модуля комплексной функции в Mathcad необходимо задать двумерную сетку аргумента. Используются два вектора: x и y, представляющие действительную и мнимую части комплексного аргумента соответственно. С помощью функции meshgrid(x, y) формируются матрицы X и Y, описывающие плоскость комплексного аргумента.
Комплексный аргумент определяется как Z := X + i·Y. Затем вычисляется значение модуля целевой функции: R := abs(f(Z)). Именно матрица R используется для построения поверхности.
Для визуализации используется компонент surface plot, доступный через вкладку «Графики». В окно построения вводятся переменные X, Y и R в качестве аргументов. Убедитесь, что размерности всех трех матриц совпадают, иначе Mathcad выдаст ошибку.
Для повышения наглядности рекомендуется включить отображение осей, применить логарифмическую шкалу к оси Z при больших значениях модуля и настроить палитру цветов для лучшей интерпретации градиента. Функция surface plot не поддерживает комплексные значения напрямую, поэтому отображается исключительно модуль функции.
На практике это позволяет анализировать особенности поведения функции, включая наличие особенностей, экстремумов и областей роста. Пример: при визуализации f(z) = 1 / (z — 1) ясно видна сингулярность в точке z = 1.
Построение цветовой карты фазы комплексной функции
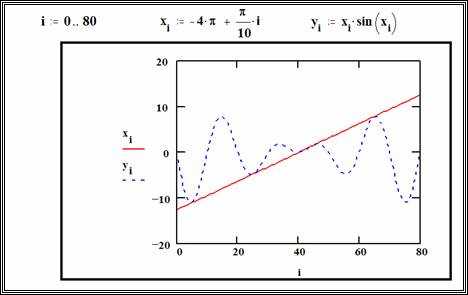
Для визуализации фазы комплексной функции f(z) = u(x,y) + iv(x,y) в Mathcad применяют цветовую карту, где каждому значению аргумента (фазы) arg(f(z)) ставится в соответствие определённый цвет. Фаза вычисляется как θ(x,y) = atan2(v, u), принимая значения в диапазоне от −π до π.
Первый шаг – создание сетки точек в области комплексной плоскости, задаваемой массивами координат x и y. На каждом узле вычисляют значение функции, затем определяют фазу с помощью встроенной функции atan2.
Для отображения фазы используется цветовой круг, часто реализуемый через модель HSV (Hue, Saturation, Value), где Hue кодирует угол фазы, а насыщенность и яркость остаются постоянными. В Mathcad следует нормировать фазу из интервала [−π, π] в диапазон [0, 1], чтобы использовать её как параметр оттенка.
Цветовая карта создаётся с помощью функции colorplot, если доступна, либо путём отображения фазового массива через графический объект с заданной цветовой шкалой. Важно обеспечить плавный переход цветов, чтобы контуры фазовых переходов были чётко различимы.
Для улучшения читаемости на графике рекомендуется добавить линию уровня или изолинии, которые соответствуют определённым значениям фазы, например 0, ±π/2, ±π. Это помогает визуально выделять ключевые точки и особенности функции.
При построении цветовой карты фазы следует учитывать размер сетки – слишком крупный шаг приводит к грубым цветовым переходам, а слишком мелкий увеличивает время вычислений без заметного выигрыша в качестве.
Заключительный этап – настройка параметров отображения, таких как масштаб осей и формат подписей, чтобы сохранить пропорции и обеспечить удобное восприятие графика без искажений.
Обработка ошибок при некорректных значениях на границах области
При построении графиков комплексных функций в Mathcad критично контролировать значения на границах области определения, поскольку именно там часто возникают ошибки вычислений и отображения.
- Проверяйте корректность входных данных с помощью условных операторов (
if,when) для исключения значений, приводящих к неопределённостям (деление на ноль, логарифм отрицательного числа, извлечение корня из отрицательного числа). - Используйте встроенные функции проверки типа и диапазона: например,
isreal()для фильтрации вещественных чисел,abs()для контроля модуля комплексных аргументов. - Для граничных точек задавайте дополнительную проверку и корректировку значений, чтобы избежать скачков или пропусков графика:
- Сглаживайте значения, близкие к границе, через ограничение диапазона (
min,max). - Вводите исключения для точек, где функция не определена, заменяя значения на
NaNили небольшое смещение. - При работе с параметрическими кривыми используйте циклы с контролем выхода за область с предупреждениями или автоматическим прекращением вычислений.
Соблюдение этих рекомендаций обеспечивает стабильность построения графиков и точное представление комплексных функций в Mathcad, исключая ложные артефакты и срывы визуализации на границах области.
Вопрос-ответ:
Как построить график комплексной функции в Mathcad?
Для построения графика комплексной функции в Mathcad нужно задать функцию, принимающую комплексное число в качестве аргумента. Затем следует разбить комплексную плоскость на сетку значений аргумента, вычислить значения функции на этой сетке и построить графики отдельно для действительной и мнимой части функции или модуля и аргумента. Для визуализации можно использовать трехмерные графики или контурные диаграммы.
Можно ли в Mathcad одновременно отобразить модуль и аргумент комплексной функции на одном графике?
Прямого способа отобразить и модуль, и аргумент комплексной функции на одном графике Mathcad не предоставляет. Обычно строят два отдельных графика: один для модуля, другой для аргумента. Однако, используя разные цвета или маркеры, можно сделать несколько графиков на одном листе, чтобы сравнить их визуально.
Как правильно задать сетку комплексных чисел для построения графика в Mathcad?
Для создания сетки комплексных чисел в Mathcad необходимо определить два диапазона: для действительной и для мнимой части переменной. Затем с помощью вложенного цикла или функции, создающей матрицу, формируют комплексные числа как комбинацию этих диапазонов. Например, если x — действительная часть, а y — мнимая, комплексное число задаётся как x + i·y. Такая сетка позволяет вычислить значения функции в каждой точке плоскости.
Какие типы графиков наиболее удобны для визуализации комплексных функций в Mathcad?
Для отображения комплексных функций часто используют трехмерные поверхности, где по осям X и Y откладываются действительная и мнимая части аргумента, а по оси Z — либо модуль, либо действительная (или мнимая) часть функции. Также популярны контурные графики, которые показывают линии равных значений модуля или аргумента. В Mathcad доступны оба варианта, что позволяет выбрать подходящий способ для конкретной задачи.